
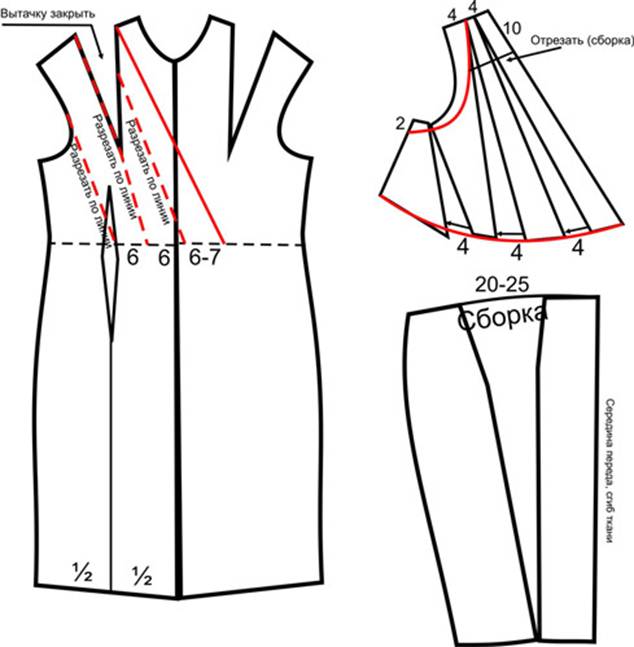
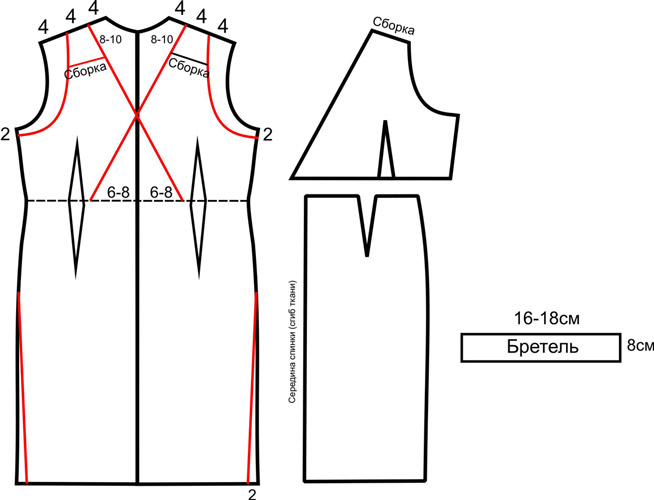
Это платье шьется из эластичного материала, поэтому застежку-молнию делать необязательно. Бретель платья кроится отдельно, шириной 8см (в готовом виде 4см) и длиной 16-18см (длину бретели необходимо отрегулировать непосредственно при примерке платья.
План теми
1. Економічна та математична постановка задачі нелінійного програмування.
2. Особливості та основні труднощі розв’язування задач нелінійного програмування.
3. Класифікація задач нелінійного програмування. Загальна характеристика методів розв’язання задач нелінійного програмування..
4. Графічний метод розв’язання задач нелінійного програмування.
5. Класичний метод оптимізації. Метод множників Лагранжа.
6. Опукле програмування.
7. Градієнтні методи. Метод Франка-Вулфа.
8. Розв’язання задач нелінійного програмування на ПЕОМ.
1. Економічна та математична постановка
задачі нелінійного програмування
Досить детально розглянута в розділах, присвячених лінійному програмуванню, задача пошуку оптимальних обсягів виробництва ґрунтується на допущеннях про лінійність зв’язку між витратами ресурсів і обсягами виготовленої продукції; між ціною, рекламою та попитом тощо. Але такі зв’язки насправді є нелінійними, тому точніші математичні моделі доцільно формулювати в термінах нелінійного програмування.
Нехай для деякої виробничої системи необхідно визначити план випуску продукції за умови найкращого способу використання її ресурсів. Відомі загальні запаси кожного ресурсу, норми витрат кожного ресурсу на одиницю продукції та ціни реалізації одиниці виготовленої продукції. Критерії оптимальності можуть бути різними, наприклад, максимізація виручки від реалізації продукції. Така умова подається лінійною залежністю загальної виручки від обсягів проданого товару та цін на одиницю продукції.
Однак, загальновідомим є факт, що за умов ринкової конкуренції питання реалізації продукції є досить складним. Обсяг збуту продукції визначається передусім її ціною, отже, як цільову функцію доцільно брати максимізацію не всієї виготовленої, а лише реалізованої продукції. Необхідно визначати також і оптимальний рівень ціни на одиницю продукції, за якої обсяг збуту був би максимальним. Для цього її потрібно ввести в задачу як невідому величину, а обмеження задачі мають враховувати зв’язки між ціною, рекламою та обсягами збуту продукції. Цільова функція в такому разі буде виражена добутком двох невідомих величин: оптимальної ціни одиниці продукції на оптимальний обсяг відповідного виду продукції, тобто буде нелінійною. Отже, маємо задачу нелінійного програмування.
Також добре відома транспортна задача стає нелінійною, якщо вартість перевезення одиниці товару залежить від загального обсягу перевезеного за маршрутом товару. Тобто коефіцієнти при невідомих у цільовій функції, що в лінійній моделі були сталими величинами, залежатимуть від значень невідомих (отже, самі стають невідомими), що знову приводить до нелінійності у функціоналі.
І нарешті, будь-яка задача стає нелінійною, якщо в математичній моделі необхідно враховувати умови невизначеності та ризик. Як показник ризику часто використовують дисперсію, тому для врахування обмеженості ризику потрібно вводити нелінійну функцію в систему обмежень, а мінімізація ризику певного процесу досягається дослідженням математичної моделі з нелінійною цільовою функцією.
Загальна задача нелінійного програмування формулюється так: знайти такий вектор 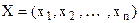 , який задовольняє систему обмежень
, який задовольняє систему обмежень
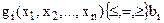 ,
, 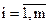 (1)
(1)
і надає екстремального значення функції
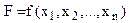 , (2)
, (2)
де всі функції 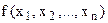 та
та 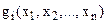 ,
, 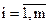 (або їх частина) є нелінійними відносно невідомих задачі.
(або їх частина) є нелінійними відносно невідомих задачі.
2. Особливості та основні труднощі розв’язування задач
нелінійного програмування
1. Для лінійних задач можна завжди знайти оптимальний розв’язок універсальним методом — симплексним. При цьому не існує проблеми стосовно доведення існування такого розв’язку, тобто в результаті застосування алгоритму симплексного методу завжди отримують один з таких варіантів відповіді:
а) отримали оптимальний розв’язок;
б) умови задачі суперечливі, тобто розв’язку не існує;
в) цільова функція необмежена, тобто розв’язку також не існує.
Для задач нелінійного програмування не існує універсального методу розв’язання, що зумовило розроблення значної кількості різних методів розв’язування окремих типів задач нелінійного програмування. Для кожного специфічного методу необхідно доводити існування розв’язку задачі та його єдиність, що також є досить складною математичною задачею.
Відомі точні методи розв’язування нелінійних задач, але в такому разі існують труднощі обчислювального характеру, тобто навіть для сучасних ЕОМ такі алгоритми є досить трудомісткими, тому здебільшого для розв’язування нелінійних задач виправданим є застосування наближених методів.
2. Для задач лінійного програмування доведено наявність єдиного екстремуму, що досягається в одній (або кількох одночасно) з вершин багатогранника допустимих розв’язків задачі. Однак у задачах нелінійного програмування існують кілька локальних оптимумів, що потребує пошуку серед них глобального.
На рис. 1 маємо на відрізку, що зображений, локальні оптимуми у точках 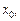
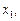
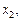
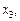
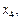
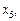
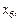
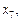
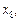
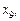 глобальний — у точках
глобальний — у точках 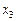 та
та 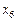 .
.
Більшість наближених методів уможливлюють, як правило, з 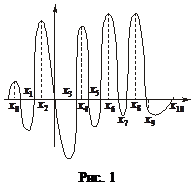 находження локального оптимуму. Можна, звичайно, користуючись простим способом, визначити всі локальні оптимуми, а потім їх зіставленням знайти глобальний. Однак для практичних розрахунків такий метод є неефективним. Часто глобальний оптимум наближені методи «не уловлюють». Наприклад, у разі, коли глобальний оптимум знаходиться досить близько біля локального. Якщо відрізок
находження локального оптимуму. Можна, звичайно, користуючись простим способом, визначити всі локальні оптимуми, а потім їх зіставленням знайти глобальний. Однак для практичних розрахунків такий метод є неефективним. Часто глобальний оптимум наближені методи «не уловлюють». Наприклад, у разі, коли глобальний оптимум знаходиться досить близько біля локального. Якщо відрізок 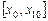 поділити на десять підвідрізків і глобальний оптимум попаде у відрізок
поділити на десять підвідрізків і глобальний оптимум попаде у відрізок 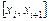 (рис. 1), а зліва від
(рис. 1), а зліва від 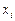 та справа від
та справа від 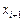 крива
крива 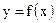 буде зростати, то глобальний оптимум буде пропущеним.
буде зростати, то глобальний оптимум буде пропущеним.
3. У задачах лінійного програмування точка оптимуму завжди була граничною точкою багатогранника допустимих планів. Для нелінійних задач точка, яка визначає оптимальний план, може бути як граничною, так і знаходитися всередині допустимої області розв’язків (планів).
4. Доведено, що множина допустимих планів задачі лінійного програмування завжди є опуклою. У разі, коли система обмежень задачі є нелінійною, вона може визначати множину допустимих розв’язків як неопуклу, або навіть складатися з довільних, не зв’язаних між собою частин.
Кожна із зазначених особливостей задач вимагає застосування специфічних методів пошуку розв’язку, тому безперечно найскладнішими для розв’язування є задачі нелінійного програмування, в яких поєднується кілька або всі згадані особливості.
3. Класифікація задач нелінійного програмування. Загальна характеристика методів розв’язання задач нелінійного програмування.
а) класичні задачі оптимізації:
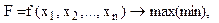 ( 3 )
( 3 )
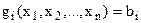 , (
, (  , ( 4 )
, ( 4 )
де функції 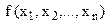 і
і 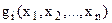 повинні бути неперервними та диференційованими і мати неперервні частинні похідні хоча б до другого порядку включно.
повинні бути неперервними та диференційованими і мати неперервні частинні похідні хоча б до другого порядку включно.
б) задачі опуклого програмування – це задачі, в яких цільова функція 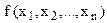 і функції обмежень
і функції обмежень 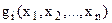 є опуклими (вгнутими) функціями.
є опуклими (вгнутими) функціями.
в) сепарабельні задачі нелінійного програмування:
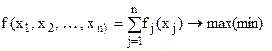 , ( 5 )
, ( 5 )
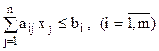 ; ( 6 )
; ( 6 )
г) квадратичні задачі нелінійного програмування :
 , ( 7 )
, ( 7 )
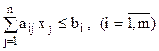 ; ( 8 )
; ( 8 )
Найбільш вивченими серед задач нелінійного програмування є задачі з нелінійною цільовою функцією та лінійними обмеженнями.
Для розв’язування задач нелінійного програмування використовуються графічні та аналітичні методи.
Аналітичні методи поділяються на:
- прямі методи;
- непрямі методи.
Прямими методами оптимальні розв’язки знаходять у напрямку найшвидшого збільшення (або зменшення) значення цільової функції. До прямих методів належать градієнтні методи.
Непрямі методи полягають у зведенні задачі до такої, знаходження екстремуму якої вдається спростити. До непрямих методів відносяться методи сепарабельного та квадратичного програмування.
Що ж стосується класичних задач оптимізації, то вони розв’язуються класичними методами з використанням апарату диференціального числення.6
4. Геометрична інтерпретація задачі
нелінійного програмування. Графічний метод розв’язання задач нелінійного програмування
Геометрично цільова функція (2) визначає деяку поверхню, а обмеження (1) — допустиму підмножину n-вимірного евклідового простору. Знаходження оптимального розв’язку задачі нелінійного програмування зводиться до відшукання точки з допустимої підмножини, в якій досягається поверхня найвищого (найнижчого) рівня.
Якщо цільова функція неперервна, а допустима множина розв’язків замкнена, непуста і обмежена, то глобальний максимум (мінімум) задачі існує.
Алгоритм знаходження розв’язку задачі нелінійного програмування графічним способом
1. Знаходиться область допустимих розв’язків, що визначається співвідношеннями ( 1 ). Якщо вона порожня, то задача не має розв’язків.
2. Будуємо лінії рівня цільової функції 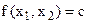 , де с – стала величина.
, де с – стала величина.
3. Визначаємо лінії найвищого (найнижчого) рівня або встановлюємо нерозв’язність задачі із-за необмеженості функції (2) зверху (знизу) на множині допустимих розв’язків.
4. Знаходимо точку області допустимих розв’язків, через яку проходить лінія найвищого (найнижчого) рівня, і обчислюємо у ній значення цільової функції ( 2 ).
Розглянемо приклад геометричного способу розв’язування задачі нелінійного програмування.
 Знайти мінімальне і максимальне значення функції:
Знайти мінімальне і максимальне значення функції:
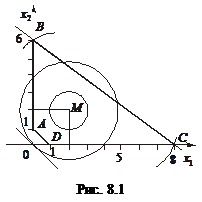
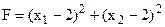
за умов:
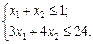
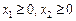 .
.
Розв’язання. Область допустимих розв’язків утворює чотирикутник АВСD (рис. 8.1). Геометрично цільова функція являє собою коло з центром у точці М (2; 2), квадрат радіуса якого 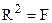 . Це означає, що її значення буде збільшуватися (зменшуватися) зі збільшенням (зменшенням) радіуса кола. Проведемо з точки М кола різних радіусів. Функція F має два локальних максимуми: точки В (0; 6) і С (8; 0). Обчислимо значення функціонала в цих точках:
. Це означає, що її значення буде збільшуватися (зменшуватися) зі збільшенням (зменшенням) радіуса кола. Проведемо з точки М кола різних радіусів. Функція F має два локальних максимуми: точки В (0; 6) і С (8; 0). Обчислимо значення функціонала в цих точках:
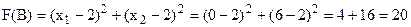 ,
,
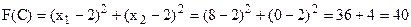 .
.
Оскільки 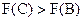 , то точка С (8; 0) є точкою глобального максимуму.
, то точка С (8; 0) є точкою глобального максимуму.
Очевидно, що найменший радіус 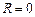 , тоді:
, тоді:
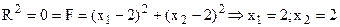 . Тобто точка М є точкою мінімуму, оскільки їй відповідає найменше можливе значення цільової функції.
. Тобто точка М є точкою мінімуму, оскільки їй відповідає найменше можливе значення цільової функції.
Зазначимо, що в даному разі точка, яка відповідає оптимальному плану задачі (мінімальному значенню функціонала), знаходиться всередині багатокутника допустимих розв’язків, що в задачах лінійного програмування неможливо.

Знайти мінімальне значення функції:
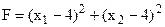
за умов:
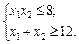
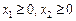 .
.
Розв’язування. У даному прикладі множина допустимих розв’язків складається з двох окремих частин, необмежених зверху (рис. 8.2). Цільова функція аналогічно попередньому випадку є колом з центром у точці М (4; 4). Функція F має два локальних мінімуми: в точці А ( 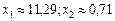 ), і в точці В (
), і в точці В ( 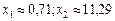 ).
).
 Значення цільової функції в цих точках однакове і дорівнює:
Значення цільової функції в цих точках однакове і дорівнює:
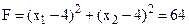 .
.
Отже, маємо два альтернативні оптимальні плани.
Даний приклад ілюструє ще одну особливість задач нелінійного програмування: на відміну від задач лінійного програмування багатогранник допустимих розв’язків задачі нелінійного програмування не обов’язково буде опуклою множиною.
5. Класичний метод оптимізації.
Метод множників Лагранжа
5.1. Задачі на безумовний
екстремум
Розглянемо задачу (1) – (2) , якщо на змінні 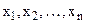 не накладаються умови обмежень. У теорії дослідження функцій такі задачі належать до задач відшукання безумовного екстремуму функції. Локальний та глобальний екстремуми тоді визначаються з необхідних та достатніх умов існування екстремуму функції.
не накладаються умови обмежень. У теорії дослідження функцій такі задачі належать до задач відшукання безумовного екстремуму функції. Локальний та глобальний екстремуми тоді визначаються з необхідних та достатніх умов існування екстремуму функції.
Нагадаємо, що необхідна умова існування локального екстремуму функції 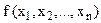 формулюється так: для того, щоб точка
формулюється так: для того, щоб точка 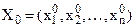 була точкою локального екстремуму, необхідно, щоб функція
була точкою локального екстремуму, необхідно, щоб функція 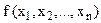 була неперервною і диференційовною в околі цієї точки і перші частинні похідні за змінними у цій точці дорівнювали нулю:
була неперервною і диференційовною в околі цієї точки і перші частинні похідні за змінними у цій точці дорівнювали нулю:
 , ( 9 )
, ( 9 )
де 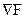 - градієнт функції F , що визначається наступним чином:
- градієнт функції F , що визначається наступним чином:
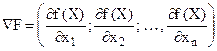 , де
, де 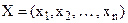 . ( 10 )
. ( 10 )
Точка 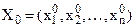 називається критичною.
називається критичною.
Щоб визначити чи критичні точки є точками екстремуму, необхідно дослідити в них частинні похідні другого порядку. Для функції 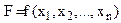 запишемо матрицю Гессе вигляду
запишемо матрицю Гессе вигляду
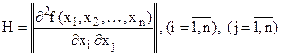 , ( 11 )
, ( 11 )
яка складається з частинних похідних другого порядку. Оскільки для неперервно-диференційованої функції мішані похідні рівні, тобто 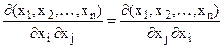 , то матриця Н – симетрична.
, то матриця Н – симетрична.
Головні мінори матриці Н позначимо таким чином:
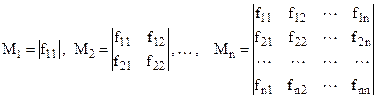 ,
,
де 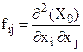 - значення частинної похідної другого порядку функції F в критичній точці
- значення частинної похідної другого порядку функції F в критичній точці 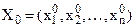 .
.
Достатня умова існування локального екстремуму формулюється так: для того, щоб критична точка 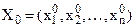 була точкою локального екстремуму, достатньо, щоб функція
була точкою локального екстремуму, достатньо, щоб функція 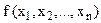 була визначена в околі критичної точки
була визначена в околі критичної точки 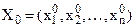 та мала в цій точці неперервні частинні похідні другого порядку.
та мала в цій точці неперервні частинні похідні другого порядку.
При цьому якщо всі головні мінори 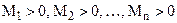 , то точка
, то точка 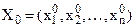 - точка локального мінімуму. Якщо головні мінори
- точка локального мінімуму. Якщо головні мінори 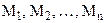 почергово міняють знак, починаючи з мінуса
почергово міняють знак, починаючи з мінуса 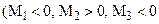 і т.д), то точка
і т.д), то точка 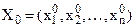 - точка локального максимуму.
- точка локального максимуму.





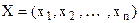 , який задовольняє систему обмежень
, який задовольняє систему обмежень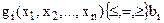 ,
, 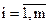 (1)
(1)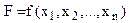 , (2)
, (2)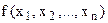 та
та 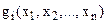 ,
, 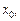
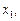
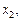
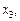
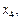
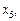
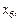
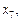
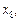
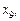 глобальний — у точках
глобальний — у точках 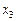 та
та 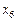 .
. находження локального оптимуму. Можна, звичайно, користуючись простим способом, визначити всі локальні оптимуми, а потім їх зіставленням знайти глобальний. Однак для практичних розрахунків такий метод є неефективним. Часто глобальний оптимум наближені методи «не уловлюють». Наприклад, у разі, коли глобальний оптимум знаходиться досить близько біля локального. Якщо відрізок
находження локального оптимуму. Можна, звичайно, користуючись простим способом, визначити всі локальні оптимуми, а потім їх зіставленням знайти глобальний. Однак для практичних розрахунків такий метод є неефективним. Часто глобальний оптимум наближені методи «не уловлюють». Наприклад, у разі, коли глобальний оптимум знаходиться досить близько біля локального. Якщо відрізок 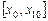 поділити на десять підвідрізків і глобальний оптимум попаде у відрізок
поділити на десять підвідрізків і глобальний оптимум попаде у відрізок 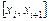 (рис. 1), а зліва від
(рис. 1), а зліва від 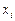 та справа від
та справа від 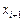 крива
крива 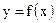 буде зростати, то глобальний оптимум буде пропущеним.
буде зростати, то глобальний оптимум буде пропущеним.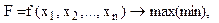 ( 3 )
( 3 )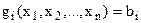 , (
, (  , ( 4 )
, ( 4 )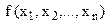 і
і 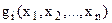 повинні бути неперервними та диференційованими і мати неперервні частинні похідні хоча б до другого порядку включно.
повинні бути неперервними та диференційованими і мати неперервні частинні похідні хоча б до другого порядку включно.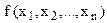 і функції обмежень
і функції обмежень 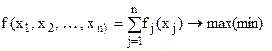 , ( 5 )
, ( 5 )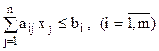 ; ( 6 )
; ( 6 ) , ( 7 )
, ( 7 )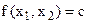 , де с – стала величина.
, де с – стала величина. Знайти мінімальне і максимальне значення функції:
Знайти мінімальне і максимальне значення функції:
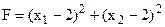
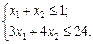
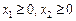 .
.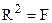 . Це означає, що її значення буде збільшуватися (зменшуватися) зі збільшенням (зменшенням) радіуса кола. Проведемо з точки М кола різних радіусів. Функція F має два локальних максимуми: точки В (0; 6) і С (8; 0). Обчислимо значення функціонала в цих точках:
. Це означає, що її значення буде збільшуватися (зменшуватися) зі збільшенням (зменшенням) радіуса кола. Проведемо з точки М кола різних радіусів. Функція F має два локальних максимуми: точки В (0; 6) і С (8; 0). Обчислимо значення функціонала в цих точках: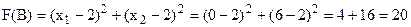 ,
,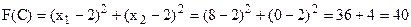 .
.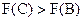 , то точка С (8; 0) є точкою глобального максимуму.
, то точка С (8; 0) є точкою глобального максимуму.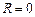 , тоді:
, тоді: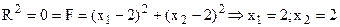 . Тобто точка М є точкою мінімуму, оскільки їй відповідає найменше можливе значення цільової функції.
. Тобто точка М є точкою мінімуму, оскільки їй відповідає найменше можливе значення цільової функції.
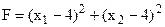
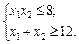
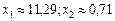 ), і в точці В (
), і в точці В ( 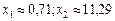 ).
). Значення цільової функції в цих точках однакове і дорівнює:
Значення цільової функції в цих точках однакове і дорівнює: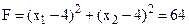 .
.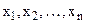 не накладаються умови обмежень. У теорії дослідження функцій такі задачі належать до задач відшукання безумовного екстремуму функції. Локальний та глобальний екстремуми тоді визначаються з необхідних та достатніх умов існування екстремуму функції.
не накладаються умови обмежень. У теорії дослідження функцій такі задачі належать до задач відшукання безумовного екстремуму функції. Локальний та глобальний екстремуми тоді визначаються з необхідних та достатніх умов існування екстремуму функції.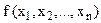 формулюється так: для того, щоб точка
формулюється так: для того, щоб точка 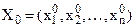 була точкою локального екстремуму, необхідно, щоб функція
була точкою локального екстремуму, необхідно, щоб функція  , ( 9 )
, ( 9 )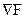 - градієнт функції F , що визначається наступним чином:
- градієнт функції F , що визначається наступним чином: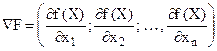 , де
, де 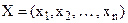 . ( 10 )
. ( 10 )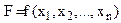 запишемо матрицю Гессе вигляду
запишемо матрицю Гессе вигляду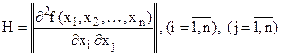 , ( 11 )
, ( 11 )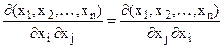 , то матриця Н – симетрична.
, то матриця Н – симетрична.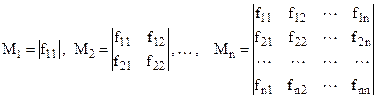 ,
,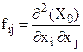 - значення частинної похідної другого порядку функції F в критичній точці
- значення частинної похідної другого порядку функції F в критичній точці 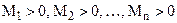 , то точка
, то точка 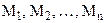 почергово міняють знак, починаючи з мінуса
почергово міняють знак, починаючи з мінуса 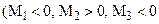 і т.д), то точка
і т.д), то точка