Задача
Нехай маємо деяку залежність y=f(x) , яка задана таблично за допомогою двох масивів: x[0], x[1], ... , x[n-1] та y[0], y[1], ... , y[n-1], де n - кількість рядків таблиці (вузлових точок). Задачею інтерполяції є побудова алгоритму, який відповідає неперервній і, по можливості, гладкій функції з інтервалом визначення [x0,xn-1], значення якої в точності відповідають наданій таблиці.
Алгоритми
Основними методами побудови інтерполяційного алгоритму є: лінійна інтерполяція, інтерполяція поліномом, інтерполяція сплайнами. Далі розглянемо найпростіший метод - лінійну інтерполяцію.
Лінійна інтерполяція виконується у два етапи:
1) знаходження номеру інтервалу, у який попадає надане значення х, тобто визначається таке i , щоб виконувалась умова: x Î [xi , xi+1] ;
2) шукане значення y(x) обчислюється по формулі: 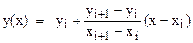 .
.
Для програмування складних задач є сенс побудувати спеціальну функцію для лінійної інтерполяції. При побудові такої функції опорну таблицю можна розміщувати або у самій функції, або зовні. У другому варіанті інтерполяційна функція буде більш універсальною, хоча і трохи менш зручною у використанні. Нижче наведено приклад саме такої функції.
// Приклад 1
double linter(double* x, double* y, int n, double t)
{ if (t<x[0] || t>x[n-1])
{ puts("Invalid value of parameter t!");
exit(0);
}
int i;
for (i=0;i<n;i++) if (t<=x[i]) break;
i--;
return y[i]+(y[i+1]-y[i])/(x[i+1]-x[i])*(t-x[i]);
}
У функції передбачено контроль правильності значення аргументу t, для якого виконується інтерполяція: згідно з правилами інтерполяції це значення не повинно виходити за межі інтервалу [x0,xn-1].


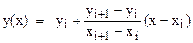 .
.