Матричні обчислення відіграють значну роль при розв’язанні прикладних задач. Вони покладені в основу математичного апарата квантової й статистичної механіки й фізики, радіоелектроніки, теорії коливань, де фундаментальне значення мають характеристичні рівняння, власні числа й вектори. Алгоритми лінійної алгебри є складовою частиною алгоритмів розв’язування дуже великої кількості лінійних і нелінійних задач моделювання і обробки даних, задач оптимізації, багатьох інших задач у наукових дослідженнях, технічних розробках, розв’язуванні економічних проблем. У даному підрозділі розглядаються декілька алгоритмів лінійної алгебри, які використовуються найбільш часто.
Звертаємо увагу на те, що у загально-математичних формулюваннях нумерація елементів масивів починається з 1, в той час як у програмних реалізаціях, які наводяться, нумерація, згідно з традиціями мови С, починається з 0.
Задача обчислення сідлової точки матриці
Задана прямокутна матриця А розміром N´M. Потрібно обчислити її мінімаксну сідлову точку за формулою :
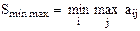 , (1)
, (1)
або максимінну сідлову точку:
 . (2)
. (2)
Алгоритм
Алгоритм випливає прямо з формул (1) і (2).
Нижче наведені дві функції, які повертають значення сідлових точок матриці з елементами типу double.
// Приклад 1
double MinMax (double** A, int N, int M )
{ int i,j; double minmax;
double* D = new double[N];// створення допоміжного масиву
for (i=0; i<N; i++)
{ D[i] = A[i][0];
for (j=1; j<M; j++) if (A[i][j]>D[i]) D[i] = A[i][j];
}
// знайти найменший серед найбільших
minmax = D[0];
for (i=1; i<N; i++) if (D[i] < minmax) minmax = D[i];
delete[] D;
return minmax;
}
// Приклад 2
double MaxMin (double** A, int N, int M )
{ int i,j; double maxmin;
double* D = new double[N];
for (i=0; i<N; i++)
{ D[i] = A[i][0];
for (j=1; j<M; j++) if (A[i][j]<D[i]) D[i] = A[i][j];
}
maxmin = D[0];
for (i=1; i<N; i++) if (D[i] > maxmin) maxmin = D[i];
delete [] D;
return maxmin;
}
Задача обчислення визначника матриці
Задана квадратна числова матриця:
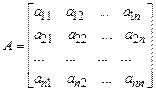 . (3)
. (3)
Обчислити її визначник det(A).
Алгоритм
До еквівалентних перетворень відносять такі перетворення, які не змінюють визначник матриці. Використовуючи певну послідовність еквівалентних перетворень, вихідну матрицю можна звести до трикутного вигляду:
 . (4)
. (4)
Визначник такої матриці легко обчислюється шляхом отримання добутку діагональних елементів:
det (A) = det (A') = 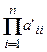 . (5)
. (5)
Якщо при виконанні перетворень матриці виконувались операції перестановки рядків, то формула для обчислення визначника дещо змінюється:
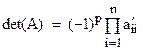 , (6)
, (6)
де p - кількість операцій парної перестановки рядків.
Для того, щоб перетворити елемент матриці akj, що лежить нижче головної діагоналі, у нуль, треба отримати нові елементи k-того рядка за такою формулою:
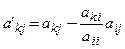 ,
, 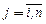 . (7)
. (7)
З останньої формули видно, що діагональний елемент aii повинен бути відмінним від нуля. Щоб цього уникнути, і, одночасно, збільшити точність і надійність обчислення визначника, застосовується прийом, названий «вибором головного елемента». Цей прийом полягає в наступному. Припустимо в i-м стовпці необхідно перетворити в нуль елементи, що лежать нижче головної діагоналі. Серед елементів цього стовпця, починаючи з aii і до останнього елемента ani, знаходимо максимальний по модулю елемент. Потім міняємо місцями i-тий рядок і рядок, що містить максимальний по модулю елемент, місцями. Таким чином, на місці діагонального елемента завжди буде максимальний (по абсолютній величині) з можливих елементів. Якщо знайдений максимальний елемент дорівнює нулю, то обчислення можна завершити: визначник у цьому випадку буде дорівнювати нулю.
Нижче наводиться приклад функції DetMatr(A,N), яка обчислює визначник матриці A розміром N´N. Обчислення виконуються відповідно до дійсного типу double.
// Приклад 3
double DetMatr(double** A, unsigned N )
{ int i, j, k=0;
double D, R;
double** C= new double*[N];// створення робочої
for (i=0; i<N; i++) C[i]=new double[N]; // матриці С
for (i=0; i<N; i++)
for (j=0; j<N; j++) C[i][j] = A[i][j];
// копіювання матриці
for (i=0; i<N-1; i++) // основний цикл
{// вибираємо головний елемент
D=fabs(C[i][i]);
k=i;
for (j=i+1; j<N; j++)
if (fabs(C[j][i])>D) { k = j; D = fabs(C[j][i]); }
// міняємо, якщо треба, рядки місцями
if (k!=i) swp(C[k],C[i]);
// перетворення в нуль елементів стовпцяR = 1./C[i][i];
for (k=i+1; k<N; k++)
{ D = C[k][i]*R;
for (j=i; j<N; j++) C[k][j] = C[k][j]- D*C[i][j];
}
}
// отримаємо визначник як добуток елементів
// головної діагоналі
D= 1.0;
for (i=0; i<N; i++) D *= C[i][i];
for (i=0; i<N; i++) delete[] C[i];// звільнення пам’яті
delete[] C;
return D;
}
Задача обчислення оберненої матриці
Надана квадратна числова матриця А з розмірами n´n. Отримати матрицю A-1, яка відповідає такій умові:
A× A-1 = A-1× A = I , (8)
де I - одинична діагональна матриця.
Алгоритм
Створимо робочу прямокутну матрицю С розміром n´2n, приписавши праворуч до вихідної матриці A одиничну діагональну матрицю E такого ж розміру:
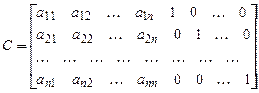 . (9)
. (9)
Виконаємо над цією розширеною матрицею перетворення, мета яких - перетворити у нулі всі елементи, що лежать нижче головної діагоналі лівої частини матриці. Операції перетворення рядків виконуємо над рядками розширеної матриці в цілому, включаючи одиничну підматрицю. Перетворення проводяться в три етапи:
1. Перетворюємо в нулі всі елементи підматриці А, які лежать нижче головної діагоналі.
2. Перетворюємо в нулі всі елементи підматриці А, що лежать вище головної діагоналі.
3. Перетворюємо всі діагональні елементи підматриці А в одиниці, шляхом ділення кожного рядка розширеної матриці на відповідний діагональний елемент.
Після виконання цих кроків, підматриця А стане одиничною, а підматриця Е перетвориться в шукану обернену матрицю А-1. У наведеному алгоритмі можна також застосувати вибір головного елемента, відповідна операція виконується на етапі 1.
Нижче наведено функцію ObrMatr, яка реалізує поданий вище алгоритм. Вхідна матриця зберігається в масиві А, зворотна записується в масив В, N - розмір матриці. Двовимірний масив B відповідних розмірів повинен бути створений заздалегідь.
// Приклад 4
void ObrMatr (double** A, double** B, unsigned N )
{ int i, j, k=0, N2=N*2;
double D, R;
double** C = new double*[N];// створення робочої матриці С
for (int i=0; i<N; i++) C[i] = new double[N2];
for (i=0; i<N; i++)
{ for (j=0; j<N; j++) { C[i][j]=A[i][j]; C[i][N+j]=0; }
C[i][i+N] = 1;
}
// зведення до нуля елементів підматриці А нижче головної
// діагоналі
for (i=0; i<N-1; i++)
{ D=fabs(C[i][i]);
k=i;
for (j=i+1; j<N; j++)
if (fabs(C[j][i])>D) { k=j; D=fabs(C[j][i]); }
if (k!=i) swp(C[k],C[i]);// вибір головного елемента
R = 1./C[i][i];
for (k=i+1; k<N; k++)
{ D = C[k][i]*R;
for (j=i; j<N2; j++) C[k][j] = C[k][j]- D*C[i][j];
}
}
// зведення до нуля елементів подматриці А вище головної
// діагоналі
for (i=0; i<N; i++)
{ D = C[i][i];
for (j=0; j<N2; j++) C[i][j]=C[i][j]/D;
}
for (i=1; i<N; i++)
for (k=0; k<i; k++)
{ D= C[k][i];
for (j=i; j<N2; j++) C[k][j]=C[k][j]-C[i][j]*D;
}
// вибір елементів оберненої матриці B
for (i=0; i<N; i++) for (j=0; j<N; j++) B[i][j] = C[i][j+N];
for (i=0; i<N; i++) delete[] C[i];// звільнення пам'яті
delete[] C;
}
Нижче наведено ще одну функцію для обернення матриці, яка реалізує так званий метод заміщення за схемою Гауса. Параметри функції: A - матриця, що надана, B - обернена матриця, N - розмір матриць А,В. Як і раніше, двовимірний масив B відповідних розмірів повинен бути створений заздалегідь. Метод заміщення є більш економним по відношенню до ресурсів пам’яті, але застосування вибору головного елемента у цьому разі неможливе.
// Приклад 5
void Minv(double** A, double** B, unsigned N )
{ int i, j, k;
double R;
for (i=0; i<N; i++) for (j=0; j<N; j++) B[i][j]=A[i][j];
for (i=0; i<N; i++)
{ R = 1./B[i][i];
for (j=0; j<N; j++) B[i][j] = B[i][j]*R;
B[i][i] = R;
for (k=0; k<N; k++)
{ if (k!=i)
{ for (j=0; j<N; j++)
if (j!=i) B[k][j]=B[k][j]-B[i][j]*B[k][i];
B[k][i] = -R*B[k][i];
}
}
}
}
Задача розв’язування системи лінійних рівнянь
Надана система лінійних рівнянь:
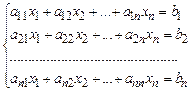 . (10)
. (10)
Треба знайти значення x1, x2, ... , xn , які задовольняють системі рівнянь.
Алгоритм
Розглянемо один з класичних методів розв’язання систем лінійних рівнянь - метод Гауса з вибором головного елемента в стовпці. Він заснований на приведенні матриці коефіцієнтів до трикутного виду.
У матричній формі система лінійних рівнянь (10) приймає такий вид:
А*Х=В , (11)
де
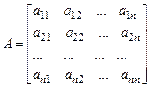 ,
, 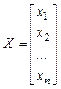 ,
, 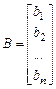 .
.
У методі Гауса використаються наступні фундаментальні властивості лінійних систем:
- перестановка рядків матриці А і відповідних елементів вектору B (тобто перестановка рівнянь у системі (10)) не змінює розв’язку системи;
- додаток до рядка елементів іншого рядка або лінійної комбінації рядків не змінює розв’язку системи.
При чисельному розв’язуванні над системою виконуються перетворення, метою яких є отримання системи з трикутною матрицею А. Після вказаного приведення виконується другий етап алгоритму - зворотній хід. Обчислення виконується по формулі:
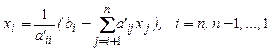 .
.
Реалізація методу Гауса у вигляді функції Gauss наведена нижче. Параметрами функції є: A - матриця системи, B - вектор правих частин, X - вектор-розв’язок системи, N - кількість рівнянь.
// Приклад 6
void Gauss(double** A, double* B, double* X, unsigned N)
{ int i, j, k=0;
double D, R;
// прямий хід
for (i=0; i<N-1; i++)
{// вибір головного елемента
D=fabs(A[i][i]);
k=i;
for (j=i+1; j<N; j++)
if (fabs(A[j][i])>D) { k=j; D=fabs(A[j][i]); }
// якщо потрібно, то поміняти місцями рядки
if (k!=i) { swp(A[k],A[i]); swp(B[k],B[i]);
// перетворення матриці у трикутну
R = 1./A[i][i];
for (k=i+1; k<N; k++)
{ D=A[k][i]*R;
for (j=i; j<N; j++) A[k][j]=A[k][j]-D*A[i][j];
B[k]=B[k]-D*B[i];
}
}
// зворотний хід
X[N-1] = B[N-1]/A[N-1][N-1];
for (i=(N-2); i>=0; i--)
{ D = 0.0;
for (j=i+1; j<N; j++) D += A[i][j]*X[j];
X[i] = (B[i]-D)/A[i][i];
}
}


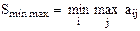 , (1)
, (1) . (2)
. (2)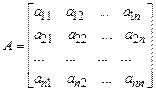 . (3)
. (3) . (4)
. (4)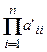 . (5)
. (5)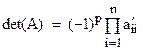 , (6)
, (6)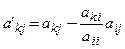 ,
, 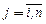 . (7)
. (7)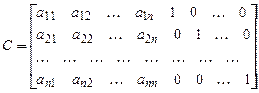 . (9)
. (9)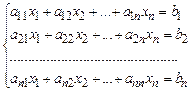 . (10)
. (10)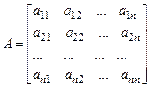 ,
, 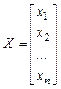 ,
, 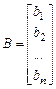 .
.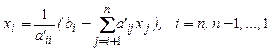 .
.