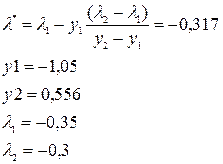Алгоритм розв”язання.
1. Розрахуємо оптимальний розмір замовлення кожного виду продукції за формулою Уілсона:
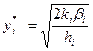 . .
2. Перевіряємо, чи виконується умова обмеження на складське приміщення:
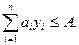 (16) (16)
Якщо так, то отримані значення 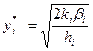 є розв’язком задачі. є розв’язком задачі.
Якщо ні – перейти до функції Лагранжа:
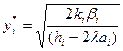 (17) (17)
де l < 0.
Зазначимо, що уі* залежить від оптимального значення l* множника Лагранжа l. Крім того, при l* = 0 значення уі* є розв’язком задачі без обмеження. Значення l* можна знайти методом систематичних проб та помилок.
У поставленій задачі мінімізації l < 0, тоді при послідовній перевірці від’ємних значень l, знайдене значення l* буде одночасно визначати значення уі*, які задовольняють задане обмеження (16) у вигляді рівності.
Таким чином, в результаті визначення l* автоматично отримуємо уі*.
Виходячи з формули (17), будується таблиця 2.
Таблиця 2
| l
| у1
| у2
| у3
| Sаіуі – А
| |
| 9,8
| 11,8
|
| 33,6
| | -0,05
| 8,9
| 10,2
| 14,1
| 19,5
| | -0,1
| 8,3
| 9,2
| 11,6
| 12,5
| | -0,15
| 7,7
| 8,3
|
| 8,1
| | -0,2
| 7,3
| 7,7
| 8,9
| 4,9
| | -0,25
| 6,9
| 7,2
| 8,1
| 2,5
| | -0,3
| 6,6
| 6,8
| 7,6
| 0,556
| | -0,35
| 6,3
| 6,4
| 7,1
| -1,05
|
При А = 28 обмеження на складське приміщення задовольняється у вигляді рівності при деякому l* (-0,3 £ l* £ -0,35). Це значення l* і його можна оцінити за допомогою лінійної інтерполяції, проводячи пряму лінію через дві точки (-0,3; 0,556) та (-0,35; -1,05). Знаходимо точку перетину прямої з віссю ОХ.
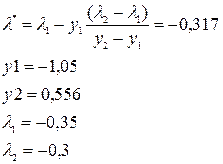
Відповідні значення уі визначають оптимальні значення обсягів замовлення продукції трьох видів:
у1* = 6,5, у2* = 6,7 та у3* = 7,4.
|


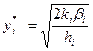 .
.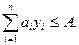 (16)
(16)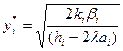 (17)
(17)