Спектры периодической последовательности
Под фазо-частотным спектром понимают совокупность их начальных фаз.
Под амплитудно-частотным спектром (АЧС) понимают совокупность амплитуд спектральных составляющих сигнала.
Для получения спектров сигналов используют следующие математические приемы:
- тригонометрические преобразования;
- разложение в ряд Фурье;
- интегральное преобразование Фурье.
Выбор того или иного приема зависит от свойств сигнала. Так, если сигнал периодический, то для его разложения на синусоидальные составляющие необходимо использовать ряд Фурье или в простейших случаях, формулы тригонометрических преобразований.
Ряд Фурье, как известно, записывается в комплексной или тригонометрической формах. Более общей является комплексная форма записи

Здесь
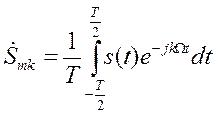 комплексная амплитуда k-того члена ряда;
комплексная амплитуда k-того члена ряда;
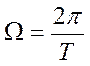 -угловая частота периодического сигнала.
-угловая частота периодического сигнала.
Тригонометрическая форма записи ряда

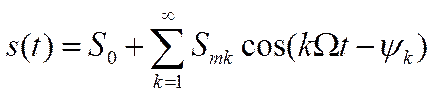
Где 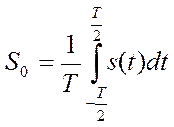 - среднее за период значение сигнала, т.е. его постоянная составляющая, которую часто называют гармоникой нулевой частоты.
- среднее за период значение сигнала, т.е. его постоянная составляющая, которую часто называют гармоникой нулевой частоты.
Полученная сумма представляет собой спектр несинусоидального периодического сигнала. Спектр является дискретным и занимает в общем случае диапазон частот 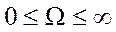 .
.
Таким образом, периодический сигнал можно рассматривать как результат наложения постоянной составляющей и бесконечно большого числа синусоидальных (гармонических) колебаний с частотами  , амплитудами
, амплитудами 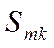 и начальными фазами
и начальными фазами 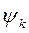 .
.
Гармонические колебания с частотами Ω, 2Ω, ЗΩ и т. д. называются соответственно основной или первой, второй, третьей и т.д. гармониками. Постоянная составляющая равна среднему значению колебания за период.
Пусть u(t) определяет периодическую последовательность прямоугольных видеоимпульсов с амплитудой Um, длительностью tИ и периодом следования 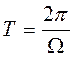 . Такие импульсы применяются, например, в радиолокации, телевидении, автоматике.
. Такие импульсы применяются, например, в радиолокации, телевидении, автоматике.
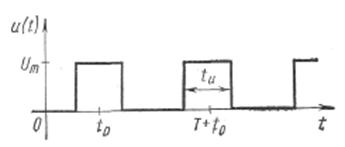
Функция u(t) в пределах периода может быть описана как
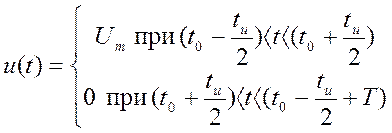
Перейдем к спектральному представлению. Проведя расчет в комплексной форме, используя формулы Эйлера и перейдя к тригонометрической форме, получим:
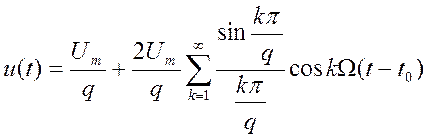
Значення амплітуд спектральних складових, тобто амплітудно – частотний спектр, розраховуємо в відповідності з формулами:
- для постійної складової (нульової гармоніки )
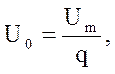
де 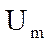 - амплітуда імпульсів;
- амплітуда імпульсів;
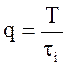 - скважність;
- скважність;
Т – період повторення імпульсів;
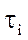 - тривалість імпульсів;
- тривалість імпульсів;
- для спектральних складових, починаючи з першої гармоніки
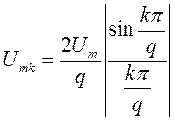
де k- номер гармоніки.
Максимальне значення k визначають
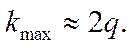
Початкові фази спектральних складових розраховують за формулою:

де 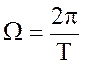 - кругова частота повторення імпульсів;
- кругова частота повторення імпульсів;
t0 - початкове зміщення сигналу (вісі симетрії першого імпульсу) відносно t=0;
n – номер арки (лепестка) спектра.
Вибір знака перед другим доданком в наведеній формулі здійснюють виходячи із зручності побудови спектра.
Графічне представлення спектрів здійснюють відрізками прямих ліній в координатах 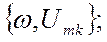
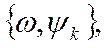 довжина яких в відповідності з вибраним масштабом визначає амплітуди і початкові фази відповідних складових.
довжина яких в відповідності з вибраним масштабом визначає амплітуди і початкові фази відповідних складових.



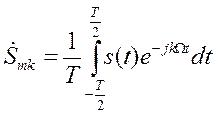 комплексная амплитуда k-того члена ряда;
комплексная амплитуда k-того члена ряда;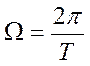 -угловая частота периодического сигнала.
-угловая частота периодического сигнала.
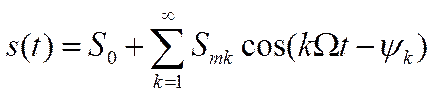
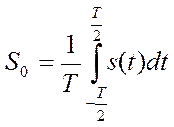 - среднее за период значение сигнала, т.е. его постоянная составляющая, которую часто называют гармоникой нулевой частоты.
- среднее за период значение сигнала, т.е. его постоянная составляющая, которую часто называют гармоникой нулевой частоты.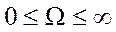 .
. , амплитудами
, амплитудами 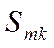 и начальными фазами
и начальными фазами 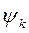 .
.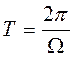 . Такие импульсы применяются, например, в радиолокации, телевидении, автоматике.
. Такие импульсы применяются, например, в радиолокации, телевидении, автоматике.
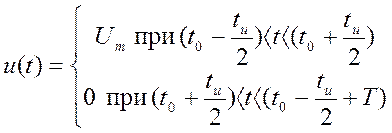
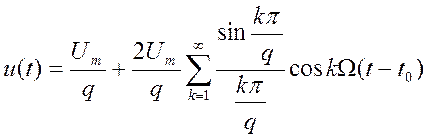
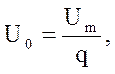
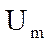 - амплітуда імпульсів;
- амплітуда імпульсів;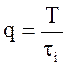 - скважність;
- скважність;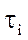 - тривалість імпульсів;
- тривалість імпульсів;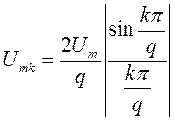
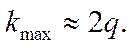

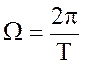 - кругова частота повторення імпульсів;
- кругова частота повторення імпульсів;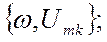
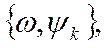 довжина яких в відповідності з вибраним масштабом визначає амплітуди і початкові фази відповідних складових.
довжина яких в відповідності з вибраним масштабом визначає амплітуди і початкові фази відповідних складових.