Задача 1.
Визначити значення функції 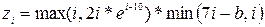 (і – номер варіанту). Задачу розв’язати двома способами: 1) не використовуючи функцію max, min; 2) визначивши та використавши функцію max, min. (і – номер варіанту). Задачу розв’язати двома способами: 1) не використовуючи функцію max, min; 2) визначивши та використавши функцію max, min.
Задача 2.
Написати програму, з використанням функції, обчислення визначеного інтегралі методами: прямокутників, Сімпсона, трапецій для обчислення визначеного інтегралу функції
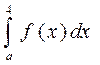
де а=0,1*N; N - номер варіанта; f(x) – підінтегральна функція, яку наведено у таблиці 1 за індивідуальними варіантами. Значення кількості інтервалів для обчислення інтеграла n -вводити з клавіатури.
Таблиця 1. Значення підінтегральних функцій
| № варіанту
| f(x)
| № варіанту
| f(x)
| |
| х3+2х2+2
|
| х3+0,2х2+0,5х+0,8
| |
| х3-3х2+9х-10
|
| х3+4х-6
| |
| х3-2х+2
|
| х3+0,1х2+0,4х-1,2
| |
| х3+3х-1
|
| х3+3х2+6х-1
| |
| х3+х-3
|
| х3- 0,1х2+0,4х-1,5
| |
| х3+0,4х2+0,6х-1,6
|
| х3-3х2+6х-2
| |
| х3-0,2х2+0,4х-1,4
|
| х3- 0,2х2+0,3х-1,2
| |
| х3-0,1х2+0,4х+2
|
| х3-3х2+12х- 9
| |
| х3+3х2+12х+3
|
| х3+0,2х2+0,5х- 2
| |
| х3-0,2х2+0,5х-1
|
| х3+3х+1
| |
| х3-0,1х2+0,4х+1,2
|
| х3+0,2х2+0,5х- 1,2
| |
| х3-3х2+6х-5
|
| х3- 3х2+9х+2
| |
| х3-0,2х2+0,5х-1,4
|
| х3- 0,1х2+0,4х-1,5
| |
| х3+2х+4
|
| х3- 3х2+6х+3
| |
| х3-3х2+12х-12
|
| х3- 0,1х2+0,3х- 0,6
|
Задача 3.
Написати програму, використовуючи рекурсивну функцію для:
1. Обчислення факторіала натурального числа.
2. Піднесення до степеня числа.
3. Обчислення суми цифр натурального числа.
4. Обчислення кількості цифр натурального числа.
5. Знаходження цифрового кореня натурального числа (цифровим коренем називається сума цифр числа, причому сума обчислюється до тих пір – поки не залишиться одна цифра).
6. Знаходження 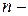 го члена арифметичної прогресії. го члена арифметичної прогресії.
7. Знаходження 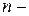 го члена геометричної прогресії. го члена геометричної прогресії.
8. Знаходження суми 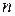 перших членів геометричної прогресії. перших членів геометричної прогресії.
9. Знаходження суми 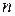 перших членів арифметичної прогресії. перших членів арифметичної прогресії.
10. Знаходження 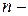 го члена послідовності Фібоначі ( го члена послідовності Фібоначі ( 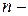 й член дорівнює сумі попереднього і наступного). й член дорівнює сумі попереднього і наступного).
|


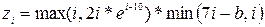 (і – номер варіанту). Задачу розв’язати двома способами: 1) не використовуючи функцію max, min; 2) визначивши та використавши функцію max, min.
(і – номер варіанту). Задачу розв’язати двома способами: 1) не використовуючи функцію max, min; 2) визначивши та використавши функцію max, min.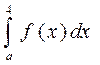
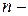 го члена арифметичної прогресії.
го члена арифметичної прогресії.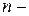 го члена геометричної прогресії.
го члена геометричної прогресії.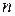 перших членів геометричної прогресії.
перших членів геометричної прогресії.