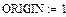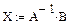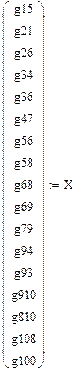1) Для задачі на знаходження екстремумів цільової функції, складеної у індивідуальному завданні № 1 (пункт 1), змінити лінійну цільову функцію на квадратичну, дописавши до попереднього виразу ще (-1)АВ  +(-1)АС +(-1)АС 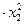 +D. Для такої задачі нелінійного програмування графічно знайти екстремуми цільової функції . +D. Для такої задачі нелінійного програмування графічно знайти екстремуми цільової функції .
2) Скласти початкові плани транспортної задачі (варіант задачі визначається порядковим номером в журналі академгрупи) за методами північно-західного кута, мінімальної вартості, подвійної переваги та апроксимації Фотеля. Вибрати з чотирьох початкових планів один і знайти оптимальний розв’язок транспортної задачі за методом потенціалів.
Варіанти завдань
1.
| Об’єми постачання, шт
Об’єми випуску, шт
|
B1=2600
|
B2=3000
|
B3=500
|
B4=1300
| |
А1=2000
|
А
|
|
|
D
| |
А2=4000
|
|
В
|
|
| |
А3=1500
|
|
|
С
|
|
2.
| Об’єми постачання, тис.т
Об’єми випуску, тис. т
|
B1=30
|
B2=60
|
B3=20
|
B4=55
| |
А1=50
|
А
|
|
|
D
| |
А2=20
|
|
В
|
|
| |
А3=75
|
|
|
С
|
|
3.
| Об’єми постачання, т
Об’єми випуску, т
|
B1=260
|
B2=210
|
B3=50
|
B4=130
| |
А1=200
|
A
|
|
|
D
| |
А2=330
|
|
B
|
|
| |
А3=150
|
|
|
C
|
|
4.
| Об’єми постачання, т
Об’єми випуску, т
|
B1=400
|
B2=650
|
B3=350
|
B4=250
| |
А1=700
|
A
|
|
|
D
| |
А2=400
|
|
B
|
|
| |
А3=500
|
|
|
C
|
|
5.
| Об’єми постачання, шт
Об’єми випуску, шт.
|
B1=1700
|
B2=3600
|
B3=6400
|
B4=2100
| |
А1=2500
|
A
|
|
|
D
| |
А2=7000
|
|
B
|
|
| |
А3=4500
|
|
|
C
|
|
6.
| Об’єми
постачання,
т
Об’єми випуску, т
|
B1=170
|
B2=360
|
B3=460
|
B4=110
| |
А1=270
|
A
|
|
|
D
| |
А2=560
|
|
B
|
|
| |
А3=330
|
|
|
C
|
|
7.
| Об’єми
постачання,
т
Об’єми випуску, т
|
B1=2400
|
B2=4300
|
B3=3600
|
B4=2100
| |
А1=6100
|
A
|
|
|
D
| |
А2=3600
|
|
B
|
|
| |
А3=2200
|
|
|
C
|
|
8.
| Об’єми
постачання,
т
Об’єми випуску, т
|
B1=80
|
B2=40
|
B3=60
|
B4=120
| |
А1=100
|
A
|
|
|
D
| |
А2=90
|
|
B
|
|
| |
А3=100
|
|
|
C
|
|
9.
| Об’єми
постачання,
т
Об’єми випуску, т
|
B1=165
|
B2=115
|
B3=170
|
B4=180
| |
А1=250
|
A
|
|
|
D
| |
А2=260
|
|
B
|
|
| |
А3=140
|
|
|
C
|
|
10.
| Об’єми
постачання,
т
Об’єми випуску, т
|
B1=30
|
B2=50
|
B3=70
|
B4=80
| |
А1=90
|
A
|
|
|
D
| |
А2=30
|
|
B
|
|
| |
А3=80
|
|
|
C
|
|
11.
| Об’єми
постачання,
т
Об’єми випуску, т
|
B1=150
|
B2=70
|
B3=100
|
B4=80
| |
А1=180
|
A
|
|
|
D
| |
А2=100
|
|
B
|
|
| |
А3=100
|
|
|
C
|
|
12.
| Об’єми
постачання,
т
Об’єми випуску, т
|
B1=150
|
B2=90
|
B3=100
|
B4=80
| |
А1=180
|
A
|
|
|
D
| |
А2=120
|
|
B
|
|
| |
А3=100
|
|
|
C
|
|
13.
| Об’єми постачання, шт
Об’єми випуску, шт.
|
B1=1000
|
B2=1500
|
B3=1600
|
B4=2100
| |
А1=2500
|
A
|
|
|
D
| |
А2=2200
|
|
B
|
|
| |
А3=1800
|
|
|
C
|
|
14.
| Об’єми
постачання,
т
Об’єми випуску, т
|
B1=350
|
B2=400
|
B3=600
|
B4=250
| |
А1=400
|
A
|
|
|
D
| |
А2=700
|
|
B
|
|
| |
А3=400
|
|
|
C
|
|
15.
| Об’єми
постачання,
тис. т
Об’єми випуску, тис.т
|
B1=90
|
B2=120
|
B3=180
|
B4=210
| |
А1=150
|
A
|
|
|
D
| |
А2=200
|
|
B
|
|
| |
А3=200
|
|
|
C
|
|
16.
| Об’єми постачання, шт
Об’єми випуску, шт
|
B1=2800
|
B2=2100
|
B3=1500
|
B4=2300
| |
А1=2500
|
A
|
|
|
D
| |
А2=3500
|
|
B
|
|
| |
А3=1500
|
|
|
C
|
|
17.
| Об’єми постачання, тис.т
Об’єми випуску, тис. т
|
B1=35
|
B2=40
|
B3=40
|
B4=50
| |
А1=40
|
A
|
|
|
D
| |
А2=70
|
|
B
|
|
| |
А3=75
|
|
|
C
|
|
18.
| Об’єми постачання, т
Об’єми випуску, т
|
B1=190
|
B2=210
|
B3=150
|
B4=230
| |
А1=200
|
A
|
|
|
D
| |
А2=350
|
|
B
|
|
| |
А3=200
|
|
|
C
|
|
19.
| Об’єми постачання, т
Об’єми випуску, т
|
B1=300
|
B2=500
|
B3=450
|
B4=350
| |
А1=400
|
A
|
|
|
D
| |
А2=450
|
|
B
|
|
| |
А3=550
|
|
|
C
|
|
20.
| Об’єми постачання, шт
Об’єми випуску, шт.
|
B1=1500
|
B2=3700
|
B3=5300
|
B4=3200
| |
А1=3000
|
A
|
|
|
D
| |
А2=6000
|
|
B
|
|
| |
А3=5500
|
|
|
C
|
|
21.
| Об’єми
постачання,
т
Об’єми випуску, т
|
B1=180
|
B2=300
|
B3=350
|
B4=230
| |
А1=210
|
A
|
|
|
D
| |
А2=560
|
|
B
|
|
| |
А3=330
|
|
|
C
|
|
22.
| Об’єми
постачання,
т
Об’єми випуску, т
|
B1=2000
|
B2=4200
|
B3=3500
|
B4=2200
| |
А1=6000
|
A
|
|
|
D
| |
А2=3600
|
|
B
|
|
| |
А3=2000
|
|
|
C
|
|
23.
| Об’єми
постачання,
т
Об’єми випуску, т
|
B1=50
|
B2=50
|
B3=80
|
B4=100
| |
А1=80
|
A
|
|
|
D
| |
А2=120
|
|
B
|
|
| |
А3=100
|
|
|
C
|
|
24.
| Об’єми
постачання,
т
Об’єми випуску, т
|
B1=230
|
B2=115
|
B3=155
|
B4=195
| |
А1=230
|
A
|
|
|
D
| |
А2=260
|
|
B
|
|
| |
А3=160
|
|
|
C
|
|
25.
| Об’єми
постачання,
т
Об’єми випуску, т
|
B1=40
|
B2=50
|
B3=60
|
B4=80
| |
А1=80
|
A
|
|
|
D
| |
А2=140
|
|
B
|
|
| |
А3=100
|
|
|
C
|
|
26.
| Об’єми
постачання,
т
Об’єми випуску, т
|
B1=150
|
B2=70
|
B3=100
|
B4=80
| |
А1=180
|
A
|
|
|
D
| |
А2=150
|
|
B
|
|
| |
А3=100
|
|
|
C
|
|
27.
| Об’єми
постачання,
т
Об’єми випуску, т
|
B1=200
|
B2=90
|
B3=100
|
B4=180
| |
А1=280
|
A
|
|
|
D
| |
А2=120
|
|
B
|
|
| |
А3=200
|
|
|
C
|
|
28.
| Об’єми постачання, шт
Об’єми випуску, шт.
|
B1=1500
|
B2=2000
|
B3=1400
|
B4=1200
| |
А1=2300
|
A
|
|
|
D
| |
А2=2200
|
|
B
|
|
| |
А3=2000
|
|
|
C
|
|
29.
| Об’єми
постачання,
т
Об’єми випуску, т
|
B1=250
|
B2=500
|
B3=600
|
B4=450
| |
А1=600
|
A
|
|
|
D
| |
А2=700
|
|
B
|
|
| |
А3=400
|
|
|
C
|
|
30.
| Об’єми
постачання,
тис. т
Об’єми випуску, тис.т
|
B1=190
|
B2=140
|
B3=180
|
B4=290
| |
А1=180
|
A
|
|
|
D
| |
А2=300
|
|
B
|
|
| |
А3=270
|
|
|
C
|
|
Матричный метод расчета ХТС
Заданные уравнения связи между параметрами входных и выходных потоков аппаратов имеют линейный вид. Уравнения материального баланса для каждого аппарата и дополнительные уравнения связи между потоками:
1) G21 – G15 = 0
2) G26 + G21 = 500
3) G34 + G36 –G93 =500
4) G34 + G94 – G47 = 0
5) G15 – G56 – G58 = 0
6) G26 + G36 + G56 – G68 – G69 = 0
7) G47 – G79 = 0
8) G58 + G68 + G108 – G810 = 0
9) G69 + G79 – G93 – G94 – G910 = 0
10) G810 + G109 – G108 –G100 = 0
11) G21 = 250
12) G34 – 0.5*G93 = 0
13) G56 – 0.5*G15 = 0
14) G68 – 0.5*G26 – 0.5*G36 – 0.5*G56 = 0
15) G93 – 0.3*G69 – 0.3*G79 =0
16) G94 – 0.4*G69 –0.4*G79 = 0
17) G108 – 0.5*G810 –0.5*G910 = 0
Для решения системы (1) ее следует привести к стандартному виду систем линейных алгебраических уравнений:
a11х1+a12х2+…..+a1nхn=bi
……. (2)
an1х1+an2х2+…..+annхn=bn
Здесь n-число уравнений и аргументов; хj-аргументы системы уравнений, в качестве которых в уравнениях (1) рассматриваются неизвестные расходы;
aij-коэффициенты системы линейных уравнений; bi-свободные члены, не содержащие неизвестных параметров.
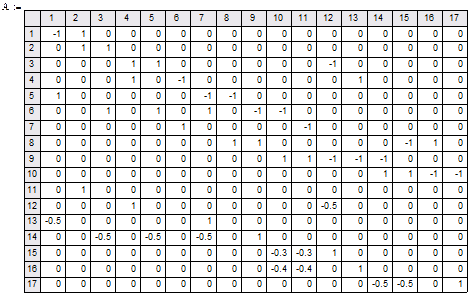
Удобно результат преобразования системы (1) к стандартному виду (2) представить в табличной (матричной, А) форме. Номер строки соответствует порядковому номеру уравнения, а номер столбца - номеру аргумента, тогда матрица коэффициентов при неизвестных расходах и вектор правых частей (свободных членов bi, B) примет вид, приведенный в таблице
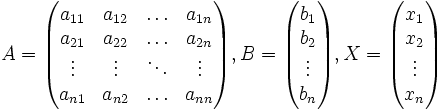

Таблица 1.
| № Ур
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
| g15
| g21
| g26
| g34
| g36
| g47
| g56
| g58
| g68
| g69
| g79
| g93
| g94
| g910
| g810
| g108
| g100
| В
|
| |
| -1
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| G02
| |
|
|
|
|
|
|
|
|
|
|
|
| -1
|
|
|
|
|
|
| G03
| |
|
|
|
|
|
| -1
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
| -1
| -1
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| -1
| -1
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
| -1
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| -1
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
| -1
| -1
| -1
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| -1
| -1
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 0,5G02
| |
|
|
|
|
|
|
|
|
|
|
|
| -0,5
|
|
|
|
|
|
| 0,5G03
| |
| -1
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
| -0,5
|
| -0,5
|
| -0,5
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
| -0,3
| -0,3
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
| -0,4
| -0,4
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
| -0,5
| -0,5
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
| -1
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| g15
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| g21
| |
|
|
|
|
|
|
|
|
|
|
| -1
|
|
|
|
|
|
|
| g26
| |
| -0
| 0,2
| 0,2
| -0,4
|
| -0,4
| -0,4
|
|
|
| -0,1
| 1,2
| 0,2
| -0,4
| 0,8
| 0,4
|
|
| g34
| |
| -0
| 0,2
| 1,2
| -0,4
|
| -0,4
| -0,4
|
|
|
| -0,1
| -0,8
| 0,2
| -0,4
| 0,8
| 0,4
|
|
| g36
| |
| -0
| 0,733
| 0,7333
| -2,47
|
| -1,467
| -1,467
|
|
|
| -0,37
| 1,7333
| 0,733
| -1,5
| 1,6
| 2,47
|
|
| g47
| |
| -1
|
|
|
|
|
|
|
|
|
| 0,5
|
|
|
|
|
|
|
| g56
| |
| -1
|
|
|
| -1
|
|
|
|
|
| 0,5
|
| -1
|
|
|
|
|
| g58
| |
| -0
| 0,6
| 0,6
| -0,2
|
| -0,2
| -0,2
|
|
|
| -0,3
| -0,4
| 0,6
| 0,8
| 0,4
| 0,2
|
|
| g68
| |
| -0
| 0,6
| 0,6
| -0,2
|
| -1,2
| -0,2
|
|
|
| -0,3
| -0,4
| 0,6
| -1,2
| 0,4
| 0,2
|
|
| g69
| |
| -0
| 0,733
| 0,7333
| -2,47
|
| -1,467
| -2,467
|
|
|
| -0,37
| 1,7333
| 0,733
| -1,5
| 1,6
| 2,47
|
|
| g79
| |
| -0
| 0,4
| 0,4
| -0,8
|
| -0,8
| -0,8
|
|
|
| -0,2
| 0,4
| 0,4
| -0,8
| 1,6
| 0,8
|
|
| g93
| |
| -0
| 0,533
| 0,5333
| -1,07
|
| -1,067
| -1,067
|
|
|
| -0,27
| 0,5333
| 0,533
| -1,1
| 0,8
| 2,07
|
|
| g94
| |
| -0
| 0,4
| 0,4
| -0,8
|
| -0,8
| -0,8
|
| -1
|
| -0,2
| 0,4
| 0,4
| -0,8
| -0,4
| -0,2
|
|
| g910
| |
| -2
| 1,6
| 1,6
| -1,2
| -2
| -1,2
| -1,2
| -2
| -1
| -2
| 0,2
| -0,4
| -0,4
| 0,8
| 0,4
| 0,2
| -2
|
| g810
| |
| -1
|
|
| -1
| -1
| -1
| -1
| -1
| -1
| -2
|
|
|
|
|
|
| -2
|
| g108
| |
| -1
|
|
| -1
| -1
| -1
| -1
| -1
| -1
| -1
|
|
|
|
|
|
|
|  1000 1000
| g100
| | | | | | | | | | Решение системы уравнений
| | | | | |  | 
| Решение системы уравнений
| | Данная таблица была сделана в Microsoft Excel, с использованием функции МОБР (выделяем количество ячеек равное нашей матрице, нажимаем F2, выбираем функцию МОБР, щелкаем на значок выбора, Ctrl+Shift+Enter).
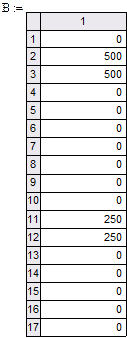
В среде Mathcad решение системы уравнений приобретает следующий вид:
|


 +(-1)АС
+(-1)АС 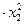 +D. Для такої задачі нелінійного програмування графічно знайти екстремуми цільової функції .
+D. Для такої задачі нелінійного програмування графічно знайти екстремуми цільової функції .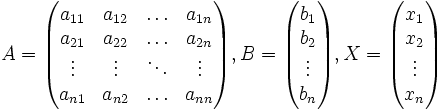

 1000
1000