оператор
Приклади умовних операторів:
а) If a >= b
then Max := a
else Max := b
б) If IntFun(i) mod 3 = 0
then write(i)
в) If (a11*a22 = a12*a21) And
((a11*b2 <> a12*b1) Or
(b1*a22 <> b2*a21))
then Write(‘ система розв’язків не має ’)
else Write(‘ система має розв’язки ’)
г) If х <= 0
then begin
u :=х*х - 2*х + 3;
v :=1/2*х + 1
end
else begin
u :=1/3*х+2;
v :=х*х+3*х-2
end
Зверніть увагу на те, що в тілі умовного оператора може використовуватись і інший умовний оператор. Це створює можливість реалізовувати багатозначне розгалуження. Наприклад:
If Discriminant < 0
then If LeadCoef < 0
then Write(‘ Розв’язків немає ’)
else Write(‘ Розв’язки - вся числова вісь ’)
else If LeadCoef < 0
then Write(‘ Розв’язки - між коренями рівняння ’)
else Write(‘ Розв’язки - поза коренями рівняння ’)
Відзначимо, що наступна конструкція мови, що складається з вкладених розгалужень синтаксично двозначна (допускає два різних варіанта синтаксичного аналізу).
If <умова 1> then If <умова 2> then <оператор 1> else <оператор 2>
1 варіант:
If < умова 1>
then begin
I f < умова 2>
then <оператор 1>
else <оператор 2>
end
2 варіант:
If< умова 1>
then begin
If < умова 2>
then <оператор 1>
end
else <оператор 2>
Для того, щоб усунути цю двозначність, в мові обрано 1-ий варіант інтерпретації у відповідності з правилом:
роздільнику else відповідає найближчий попередній роздільник then.
6.4. Приклади
Програмами, що розгалужуються, називаються програми, в яких використовуються оператори розгалуження.
Приклад 6.1. Скласти програму розв’язання квадратного рівняння, заданого своїми коефіцієнтами a, b, c.
Program SquareEquation;
Const
Line = ‘----------------------------‘;
Var
a, b, c, Root1, Root2: real;
Solution: Integer;
Procedure InpData (Var a, b, c : Real);
Begin
Write(‘ Введіть коефіцієнти рівняння (через пробіл):’);
Readln(a, b, c) ;
End;
Procedure SolutionEquation ( a, b, c : Real; Var Solution: Integer; Var Root1, Root2: real );
Var Discriminant: Real;
Begin
Discriminant := Sqr(b) - 4*a*c;
If Discriminant < 0
then Solution := 0 { Немає коренів }
else If Discriminant = 0 { Один корінь }
then begin
Solution := 1;
Root1 := -b/a;
end
else { Два кореня } begin
Solution := 2;
Root1 := (-b + Sqrt(Discriminant))/(2*a);
Root2 := -b/a - Root1;
end ;
End;
Procedure OutData (Solution, Root1, Root2: Real);
Begin
Writeln(Line);
Writeln(‘ Кількість розв’язків дорівнює: ‘, Solution);
If Solution=1 then Writeln(‘ X= ‘,Root1);
If Solution=2 then Writeln(‘ X1= ‘,Root1, ‘ X2= ‘,Root2);
End;
Begin
{Введення даних}
InpData (a, b, c);
{Обчислення}
SolutionEquation ( a, b, c, Solution, Root1, Root2);
OutData (Solution, Root1, Root2l);
End.
6.5. Задачі вибору й упорядкування
6.5.1. Задачі вибору
У найбільш простих випадках, коли є невелика кількість елементів інформації, пошук елемента з заданими властивостями зводиться до вибору цього елемента з декількох елементів. Тому такі задачі називають задачами вибору.
Задача 1. Вибір мінімального з двох елементів. У задачі потрібно з двох елементів a і b вибрати мінімальний.
Розв’язання. Вибір мінімального елемента з двох даних a і b програмується як розгалуження:
If a < b then Min := a else Min := b
Оскільки такий вибір в інших алгоритмах використовується дуже часто, мовою програмування його реалізують у вигляді функції
Function Min(a, b: Real): Real;
Begin
If a < b
then Min := a
else Min := b
End;
Цей алгоритм, власне кажучи, не залежить від того, з якими даними він має справу. Порівнювати за величиною можна цілі, дійсні або раціональні числа. Символи і рядки порівнюють згідно з алфавітним порядком. Якщо в якості даного використовується сукупність відомостей про учня, мірою порівняння може бути його вік, зріст або рейтинг успішності.
Таким чином, у наведеній функціі тип даних легко можна змінити на необхідний.
Задача 2. Вибір мінімального з трьох елементів. У задачі потрібно з елементів a, b, с вибрати мінімальний елемент d.
Розв’язання. Вибір мінімального елемента з трьох даних елементів можна здійснити, використовуючи функцію Min:
d := Min(Min(a, b), c);
Текст програми мовою Паскаль:
Program Min;
Var
a, b, c : Real;
d : Real;
Function Min (u, v: Real): Real;
Begin
If u < v
then Min := u
else Min := v
End;
Begin
{введення a, b, c}
d := Min(Min(a, b), c);
{виведення d}
End.
Задачі для самостійного розв’язування.
Задача 3. Скласти алгоритм вибору найменшого і найбільшого з двох елементів. Скільки операцій порівняння виконує Ваш алгоритм?
Задача 4. Скласти алгоритм вибору найбільшого з трьох елементів. Скільки операцій порівняння виконує Ваш алгоритм?
Задача 5. Скласти алгоритм вибору найменшого і найбільшого з чотирьох елементів. Скільки операцій порівняння виконує Ваш алгоритм?
Задача 6. Відомо, що в множині з 4-х елементів a1 < a2, a3 < a4. Скласти алгоритм пошуку найменшого елемента в цій множині. Скільки операцій порівняння виконує Ваш алгоритм?
6.5.2. Дерево розв’язувань задачі вибору
Розглянемо можливі постановки задачі вибору з трьох елементів. Вибрати максимальний із трьох елементів можна так само, як мінімальний. Інша справа, якщо з трьох елементів потрібно вибрати середній за величиною.
Задача 7. Вибір середнього з трьох елементів. Дано попарно нерівні елементи a, b, c. Вибрати з них середній за величиною.
Розв’язання. Розглянемо всі можливі варіанти розташування цих елементів у порядку зростання:
1. a < b < c, 2. a < c < b, 3. b < a < c, 4. b < c < a, 5. c < a < b, 6. c < b < a
Логічний аналіз задачі зручно зобразити у виді графічної схеми (рис 6.1)
Якщо в нашому алгоритмі використовувати порівняння a < b, у випадках 1, 2, 5 виконання піде по гілці «так», у випадках 2., 3., 6. – по гілці «ні». Використовуємо тепер у нашому алгоритмі порівняння a < c як по гілці «так», так і по гілці «ні».
a < b Гілка «так»
a < c гілка “так” (1. a < b < c, 2. a < c < b), a < c гілка “ні” 5. c < a < b
a < b Гілка «ні»
a < c гілка “так” ( 3. b < a < c, ) a < c гілка “ні” ( 4. b < c < a,) 6. c < b < a)
Тепер ясно, що для того, щоб зробити остаточний вибір, необхідно в алгоритм включити і третє порівняння b < c.
Рис 6.1. Дерево рішень задачі вибору середнього з трьох елементів.
Такі схеми називають деревом рішень задачі вибору. Графічними елементами дерева рішень є вершини і дуги. Для кожної вершини дерева зазначені:
· сукупність варіантів, що можливі в даній вершині;
· порівняння, що застосовується до даних, коли виконання алгоритму проходить через цю вершину.
Кожній дузі відповідає одне з двох логічних значень «Так», «Ні» – результат порівняння даних у цій вершині. Напрямок, зазначений на дузі стрілкою, указує шлях виконання алгоритму вибору.
Виконання алгоритму починається у початковій вершині (корені дерева) і продовжується по тій або іншій гілці дерева в залежності від результату порівняння.
Задача вибору розв’язана, якщо всі сукупності варіантів містять рівно один варіант.
Аналіз розв’язування задачі про середній із трьох елементів дозволяє зробити висновок: Будь-який алгоритм її розв’язування в гіршому випадку повинен виконати три порівняння.
Якщо дерево рішень побудовано, відповідна програма мовою Паскаль пишеться відповідно до цього дерева, причому кожній вершині відповідає оператор розгалуження:
Текст процедури мовою Паскаль:
Procedure Middle(a, b, c : Real; Var Mid : Real);
Begin
If a < b
Then If a < c
Then If b < c
Then Mid := b {варіант 1}
Else Mid := c {варіант 2}
Else Mid := a {варіант 5}
Else If a < c
Then Mid := a {варіант 3}
Else If b < c
Then Mid := c {варіант 4}
Else Mid := b {варіант 6}
End;
6.5.3. Задачі на зважування
У задачах на зважування потрібно вибрати з декількох предметів (наприклад, монет) той, який відрізняється за вагою від інших (фальшиву монету). Для порівняння предметів використовуються чашкові терези без гирь. За допомогою цього приладу можна визначити, що два предмети рівні, або з'ясувати, який з них легше. Так само можна діяти і з двома групами предметів. Як правило, порівнювати дві групи предметів має сенс тоді, коли в них рівна кількість елементів. У задачах на зважування потрібно знайти розв’язок за найменшу кількість зважувань.
Чашкові терези, що порівнюють два предмети – елемента можна запрограмувати за допомогою наступної функції:
Function Compare(A, B : Real):Integer;
Begin
If A < B
Then Compare := -1
Else If A = B
Then Compare := 0
Else Compare := 1
End;
Задача 8. Дано три однакові на зовнішній вигляд монети. Відомо, що серед них є одна фальшива, котра ледве відрізняється за вагою від інших. Знайти за допомогою чашкових вагів фальшиву монету, якщо відомо, що вона легше, ніж справжні.
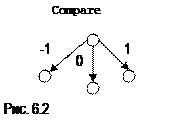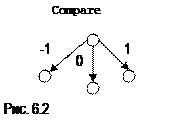Розв’язання. Будуємо дерево розв’язків, вершини якого мають три розгалуження (Рис.6.2).
