Функції

Зверніть увагу на те, яким чином визначено тип значення функції.

Таким чином, для функції визначені всі ті поняття, які були сформульовані для процедур.

Ім’я, що задане в заголовку функції, іменує цю функцію. В середині описання функції – в розділі операторів – повинно бути присвоювання, в лівій частині якого стоїть ім’я функції, а в правій – вираз що має тип значення функції.

5.5. Приклади

Приклад 5.3. Функція GCD (алгоритм Евкліда) обчислює найбільший спільний дільник двох натуральних чисел х і у.

Function GCD (x, y : Integer) : Integer ;

Begin

While x <> y do

If x < y

then y := y - x

else x := x - y ;

GCD := x

End;

Приклад 5.4. Функція IntPow підносить дійсне число x до цілого степеня N. (Y = x ^N )

Function IntPow(x: Real; N: Integer) : Real;

Var

i: Integer;

Begin

IntPow := 1;

For i:=1 to Abs(N) do IntPow := IntPow * x;

If N < 0 then IntPow := 1/IntPow

End;

Приклад 5.5. Програма обчислює найбільший спільний дільник послідовності натуральних чисел, яка представлена масивом.

Program GCD_of_Array;

Const

n = 100 ;

Var

i, D : Integer;

A : Array[1..n] of Integer;

Function GCD (x, y : Integer) : Integer ;

Begin

While x <> y do

If x < y

then y := y - x

else x := x - y;

GCD := x

End;

Begin { основна програма }

{Процедура читання масиву натуральних чисел}

D := GCD (A[1], A[2]);

For i := 3 to n do D := GCD(D, A[i]);

writeln ( ‘ НCД послідовності = ‘ , D )

End.

Кожна процедура або функція може, в свою чергу, містити розділ процедур і функцій, в якому визначені одна або декілька процедур і функцій. В цьому випадку кажуть про вкладення процедур. Кількість рівнів вкладень може бути довільною. Структура вкладення ілюструється рисунком:

Main

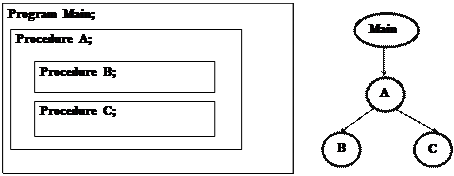
A

Поняття локальних і глобальних об’єктів поширюються і на вкладені процедури. Наприклад, змінна, описана в процедурі А локальна по відношенню до основної програми і глобальна для процедур В і С, вкладених в А.

В деяких випадках необхідно з процедури здійснити виклик іншої процедури, описаної в тому ж розділі процедур і функцій. Наприклад, процедура С може містити оператор виклику процедури В. В цьому випадку компілятор правильно обробить текст програми, оскільки процедура В описана до процедури С. Якщо ж з процедури В необхідно звернутись до С, для правильної обробки виклику С необхідно використовувати механізм так званого попереднього описання С. Описання, що опереджає процедури (функції) – це її заголовок, услід за яким через “;” стоїть службове слово Forward. У тексті програми описання, що опереджає, повинно передувати процедурі, в якій процедура, що попередньо описана, викликається.

Якщо процедура або функція описані попередньо, описанню її тіла передує скорочений заголовок, що складається тільки з відповідного службового слова і імені – без списку описань параметрів.

Procedure A (x : TypeX; Var y : TypeY); Forward;

Procedure B (z : TypeZ) ;

Begin

... A( p, q); ...

End;

Procedure A;

Begin

...

End;

6. ПРОГРАМУВАННЯ РОЗГАЛУЖЕНЬ

6.1. Поняття умови. Тип даних Boolean (логічний)

Умови використовуються в програмах для організації розгалужень і дій, що повторюються. Умовою в мові є логічний вираз - вираз типу Boolean. Булевські значення – це логічні істинностні значення: : True (істина) і False (хибність).

Цей тип даних, як і інші прості типи даних, упорядкований. На ньому визначені функції Ord, Succ, Pred.

Таким чином, мають місце наступні співвідношення:

False < True ,

Ord (False)=0, Ord (True)=1,

Succ (False)=True, Pred (True)=False.

На множині < False, True > визначені логічні операції.

Операції:

And - логічна кон’юнкція ( і )

Or - логічна диз’юнкція ( або )

Not - логічне заперечення ( ні )

Ці операції визначаються наступними таблицями істинності:

Відношення, що були визначені раніше для простих стандартних типів є операціями, результат яких має логічний тип. Іншими словами, булевське значення дає будь-яка з операцій відношень : =, < > , <= , < , > , >= , in.

Для типу Boolean визначені стандартні функції, які приймають значення цього типу (логічні значення):

Odd(Х)

{ Odd(Х) = True, якщо Х - ціле непарне число

Odd(Х) = False, якщо Х - ціле парне число

}

Eoln(F) { кінець рядка в текстовому файлі}

Eof(F) { кінець файла}

Функції Eoln(F) і Eof(F) ми розглянемо при вивченні файлів.

Умови можна класифікувати як прості і складені. Прості умови визначені діаграмою:

Проста

Умова

Складені умови конструюються з простих за допомо­гою логічних операцій.

Наведемо приклади простих і складених виразів типу Boolean (умов).

Прості вирази типу Boolean (умови):

Sin(2*x) > Ѕ, (X + Y) mod Prime = 0,

b*b >= 4*a*c ,

Number div Modulo = 2,

Odd(A*P + B),

Flag ;

Складені вирази типу Boolean (умови) :

а) (а + i > b) or ( х [Index] = с ) {а, b, с - змінні типу Real, х - масив дійсних чисел , Index - змінна типу Integer }

б) Odd (n) And (n < 10е4)

в) Eof(f) Or (c = 0) {f - файл дійсних чисел}

г) Not(beta) And (gamma) {beta і gamma - змінні типу Boolean}

д) (A > B) = (C > D)

Логічні вирази перетворюються за законами логіки висловлювань. Наприклад,

Not((A > 0) And (B <> 0)) <==>

Not(A > 0) Or Not(B <> 0) <==>

(A <= 0) Or (B = 0)

Перетворення логічних виразів часто приводять до зменшення їх складності і, тим самим, оптимізації програми за часом.

6.2. Складений оператор

Декілька операторів, що виконуються послідовно, можна об’єднувати в один складений оператор.

Складений оператор передбачає виконання операторів, які в нього входять (компонент) у порядку їх написання. Службові слова Begin і End грають роль дужок операторів – вони виділяють тіло складного оператора.

Складений оператор визначається діаграмою: