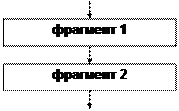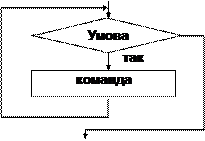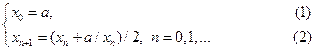Розробляючи цей алгоритм, ми спиралися на його неформальний опис, викладений у виді методу рішення задачі. Програмування таких методів і є головною роботою програміста.
Після того, як метод знайдений і визнаний підходящим, програміст має описати його в системі команд виконавця, тобто закодувати. Методика, яку ми показали, називається методом послідовних уточнень .
Справді, ми почали з відповіді на таке питання: що дано і що потрібно знайти. Уточнення входу і виходу у виді описів величин – один з найважливіших етапів розробки алгоритмів.
Далі, на кожному кроці побудови алгоритму ми уточнювали одну з дій методу рішення задачі як команду або умову. Така дисципліна дозволяє обмежити міркування відповідями на такі питання:
Який спосіб управління потрібно зараз застосувати?
Чи можна реалізувати дію однією командою виконавця?
Як сформулювати умову?
Програміст, який усвідомлено застосовує метод послідовних уточнень, заощаджує свій час, радує начальство якістю і швидкістю роботи, допускає мало помилок і створює програми, які легко читати іншим програмістам.
1.13. Базові структури управління
Основним досягненням теорії програмування 60-х років є усвідомлення і теоретичне осмислення того факту, що існують декілька основних (базових) способів управління обчисленнями, використовуючи які можна описати будь-який алгоритмічний метод рішення задачі. Структура управління будь-якого алгоритму може бути реалізована у виді комбінації основних структур управління. Ці способи управління, або структури управління, нам уже відомі. До них відносяться:
· послідовне виконання
· розгалуження
· повторення з передумовою
Таким чином, замість програмування в системі команд - блоків Обчислення, Умова і Стрілка Перейти, можна програмувати в структурах управління, причому швидкодія алгоритмів при цьому не погіршується, а такі властивості, як зрозумілість («читабельність») алгоритму істотно поліпшуються. Ефект спагеті не може проявитися тому, що кожна зі структур управління має тільки один вихід.
| | | | |
| | |  |
| | | Алгоритм Евкліда;
Вхід A, B;
Вихід: D;
{Коментар: D = НСД (AB)}
A, B: НАТ;
D: НАТ;
Початок
Поки A ¹ B виконати
Якщо A < B
то B := B - A
інакше A := A - B;
D := A
Кінець.
| |
| |
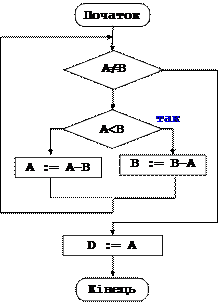
Рис 1.10. Текст і блок-схема алгоритму Евкліда.
Порівняйте текст і блок схему алгоритму Евкліда (рис 1.9): структурований текст представляє алгоритм не менш виразно, ніж його блок-схема. Текст до того ж містить багато корисної інформації, яку не можна виразити в графічних образах. Це відноситься, наприклад, до опису величин.
Розглянемо алгоритм наближеного обчислення кореня квадратного з невід’ємного дійсного числа. Цей алгоритм спирається на метод наближених обчислень, представлений формулами
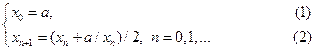
де a – позитивне число, з якого потрібно обчислити корінь.
Ці формули потрібно розуміти так:
Обчислення починаються зі значення x = a (формула (1)).
На кожному кроці поточне значення x підставляється в праву частину формули (2) і обчислюється нове значення x.
Якщо нове значення x відрізняється від старого на величину більшу, ніж точність обчислень, обчислення по формулі (2) повторюється. У противному випадку обчислення закінчене.
У формулах методу число n відіграє роль лічильника числа кроків .
Запишемо цей алгоритм:
Алгоритм КвКорінь;
Вхідa, t: ДІЙСН;
Вихідy: ДІЙСН;
Допx: ДІЙСН;