Розберемо розв’язок однієї задачі оптимального виробничого планування (або задачі про використання ресурсів).
Змістовна постановка задачі. Для виготовлення взуття двох моделей на фабриці використовується два сорти шкіри. Тижневі ресурси робочої сили і матеріалу, витрати праці і матеріалу для виготовлення кожної пари взуття, а також прибуток від реалізації одиниці продукції наведені в таблиці.
| Ресурси
| Норми витрат ресурсів на один виріб
| Загальний запас ресурсів
|
| №1
| №2
|
| Рабочий час (люд.-год)
Шкіра I сорту (шмат.)
Шкіра II сорту (шмат.)
|
-
|
|
|
| Прибуток (грн.)
|
|
|
|
Скласти план випуску взуття в асортименті, що максимізує щотижневий прибуток.
Розв’язання. Спочатку складемо математичну модель поставленої задачі. Вона містить у собі змінні задачі, цільову функцію і систему обмежень.
Змінні задачі. Оскільки в задачі потрібно скласти тижневий план випуску взуття, то змінними задачі є:
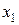 пар взуття – тижневий план випуску моделі №1,
пар взуття – тижневий план випуску моделі №1,
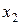 пар взуття – тижневий план випуску моделі №2.
пар взуття – тижневий план випуску моделі №2.
Цільова функція задачі. Оскільки прибуток від випуску 1 пари взуття моделі №1 складає 50 грн., а моделі №2 – 70 грн., то загальний тижневий прибуток від випуску 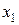 пар взуття моделі №1 і
пар взуття моделі №1 і 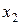 пар взуття моделі №2 складатиме
пар взуття моделі №2 складатиме 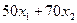 (грн.). Таким чином, цільова функція задачі, яку необхідно максимізувати, має вигляд
(грн.). Таким чином, цільова функція задачі, яку необхідно максимізувати, має вигляд
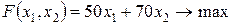 .
.
Система обмежень задачі. З урахуванням наведених у таблиці даних можна скласти такі обмеження у вигляді нерівностей.
· Робочий час, затрачуваний на випуск запланованого взуття, складає 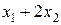 (люд.-год.). З урахуванням загального фонду робочого часу в 900 люд.-год., який не можна перевищити, одержимо нерівність:
(люд.-год.). З урахуванням загального фонду робочого часу в 900 люд.-год., який не можна перевищити, одержимо нерівність:
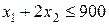 .
.
· Витрата шкіри I сорту (у шматках) на виготовлення запланованої партії взуття представиться за аналогією з попередньою нерівністю:
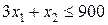 .
.
· Витрата шкіри II сорту (у шматках) – відповідно:
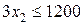 .
.
Якщо обидві частини останньої нерівності поділити на 3, то одержимо:
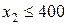 .
.
· План випуску взуття за смислом не може набувати від’ємних значень, тому останнє обмеження невід’ємності змінних:
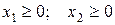 .
.
Таким чином, математична модель задачі має вигляд:
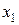 пар взуття – тижневий план випуску моделі №1,
пар взуття – тижневий план випуску моделі №1,
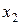 пар взуття – тижневий план випуску моделі №2,
пар взуття – тижневий план випуску моделі №2,
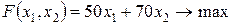
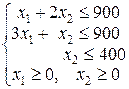
Математична модель виражається через дві змінні, тому для розв’язання задачі можна застосовувати графічний метод.
На координатній площині 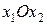 зобразимо множину точок
зобразимо множину точок 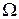 , координати яких задовольняють системі обмежень. Ця множина називається областю припустимих розв’язків (областю припустимих значень).
, координати яких задовольняють системі обмежень. Ця множина називається областю припустимих розв’язків (областю припустимих значень).
Спочатку зауважимо, що система обмежень містить нерівності 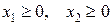 , які означають, що шукана область
, які означають, що шукана область 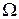 лежить у першій чверті. Далі побудуємо прямі
лежить у першій чверті. Далі побудуємо прямі
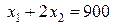 , (1)
, (1)
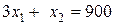 , (2)
, (2)
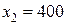 . (3)
. (3)
Для цього знайдемо по дві пари точок, через які проходить кожна з цих прямих:
1. 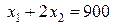 : (0, 450), (900, 0);
: (0, 450), (900, 0);
2. 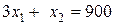 : (0, 900), (300, 0);
: (0, 900), (300, 0);
3. 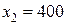 : (0, 400), (500, 400).
: (0, 400), (500, 400).
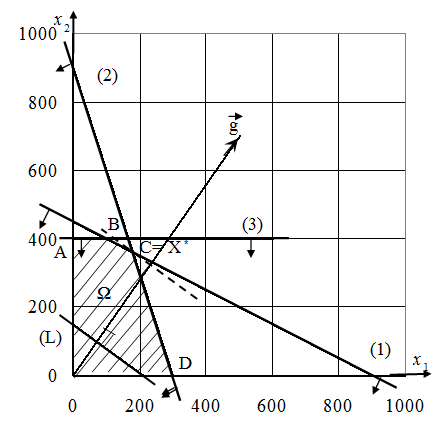
Ці прямі з відповідними мітками зображені на рис. 1.1.
Множина точок, які задовольняють нерівності 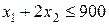 , являє собою півплощину, що обмежена прямою
, являє собою півплощину, що обмежена прямою 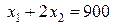 . Оскільки точка О(0,0) задовольняє нерівності (
. Оскільки точка О(0,0) задовольняє нерівності ( 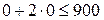 - вірно), то шукана півплощина містить цю точку; це зображено на рис. 1.1 за допомогою стрілок. Аналогічно, точка О(0,0) задовольняє кожній із нерівностей
- вірно), то шукана півплощина містить цю точку; це зображено на рис. 1.1 за допомогою стрілок. Аналогічно, точка О(0,0) задовольняє кожній із нерівностей 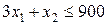 і
і 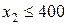 , тому ця точка міститься у відповідних півплощинах (див. рис. 1.1). З урахуванням розташування в першій чверті область припустимих розв’язків
, тому ця точка міститься у відповідних півплощинах (див. рис. 1.1). З урахуванням розташування в першій чверті область припустимих розв’язків 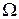 являє собою заштрихований многокутник OABCD.
являє собою заштрихований многокутник OABCD.
|
| Рис. 1.1 – Розв’язання задачі лінійного програмування графічним методом
|
Тепер зобразимо вектор 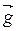 найшвидшого росту цільової функції
найшвидшого росту цільової функції 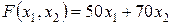 , яким є вектор, співспрямований її градієнту. Координатами вектора градієнта (для лінійної відносно змінних функції) є коефіцієнти при змінних цільової функції, тобто
, яким є вектор, співспрямований її градієнту. Координатами вектора градієнта (для лінійної відносно змінних функції) є коефіцієнти при змінних цільової функції, тобто 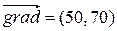 . Як вектор
. Як вектор 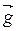 оберемо для зручності побудови вектор
оберемо для зручності побудови вектор
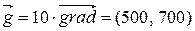 .
.
Для зображення цього вектора з'єднуємо спрямованим відрізком точки з координатами (0, 0) і (500, 700). Довільна лінія рівня цільової функції (L) проходить перпендикулярно до вектора 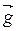 .
.
Для пошуку точки області припустимих розв’язків, у якій цільова функція досягає свого максимуму (мінімуму), необхідно лінію рівня пересувати в напрямку вектора градієнта (відповідно у зворотному напрямку). Крайня точка 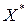 області
області 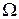 при такому русі буде відповідати оптимальному розв’язку. У даній задачі такою точкою
при такому русі буде відповідати оптимальному розв’язку. У даній задачі такою точкою 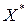 буде точка С. Знайдемо її координати, зауваживши, що вона є точкою перетинання прямих (1) і (2). Тому розв’яжемо систему
буде точка С. Знайдемо її координати, зауваживши, що вона є точкою перетинання прямих (1) і (2). Тому розв’яжемо систему
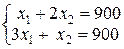 .
.
Із першого рівняння виразимо 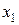 :
:
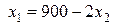 . (4)
. (4)
Потім підставимо знайдений вираз у друге рівняння:
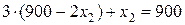 ,
,
звідки одержимо
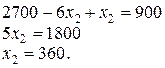
Знаючи 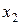 , за допомогою (4) знаходимо
, за допомогою (4) знаходимо 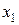 :
:
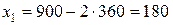 .
.
У результаті дійдемо висновку, що 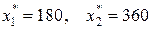 , а точка, яка відповідає оптимальному розв’язку, має координати
, а точка, яка відповідає оптимальному розв’язку, має координати 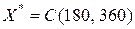 . Максимальне значення цільової функції:
. Максимальне значення цільової функції:
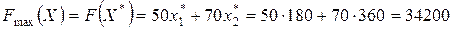 (грн.).
(грн.).
Відповідь. Для одержання максимального тижневого прибутку, що складає 34200 грн., фабрика повинна випускати 180 пар взуття моделі №1 і 360 пар взуття моделі №2 за тиждень.
2 Розв’язання задач лінійного програмування за допомогою інструмента “Поиск решения”
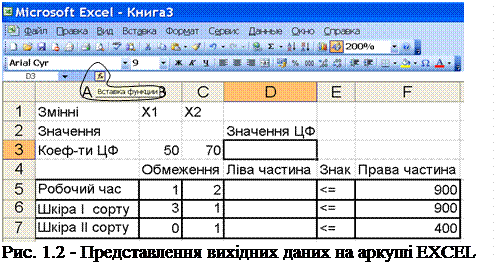
Відповідно до математичної моделі поставленої задачі підготуємо аркуш EXCEL для застосування інструмента «Поиск решения» (див. рис. 1.2):
1) комірки В2:C2 резервуємо для оптимальних значень змінних 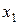 і
і 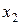 (оптимального плану задачі), що будуть знайдені як результат застосування процедури «Поиск решения»;
(оптимального плану задачі), що будуть знайдені як результат застосування процедури «Поиск решения»;
2) комірку D3 резервуємо для значення цільової функції на оптимальному плані;
3) у комірки В3:C3 вносимо значення коефіцієнтів цільової функції;
4) комірки В5:С5, В6:С6, В7:С7 заповнюємо коефіцієнтами при змінних у лівій частині відповідних обмежень;
5) у комірки F5:F7 записуємо значення правих частин відповідних обмежень;
6) у комірки Е5:Е7 вносимо знак нерівності у відповідному обмеженні;
7) комірки D5:D7 резервуємо для значень лівих частин системи обмежень на оптимальному плані.
Внесемо формули, помітивши, що значення цільової функції (комірка D3) дорівнює сумі добутків[1] невідомих значень змінних (комірки В2:С2) на коефіцієнти цільової функції (комірки В3:C3), а значення лівих частин системи обмежень (комірки D5, D6 і D7) дорівнюють сумі добутків невідомих значень змінних (комірки В2:С2) на коефіцієнти лівих частин системи обмежень (комірки В5:С5, В6:С6, В7:С7 відповідно). Для цього в цільову комірку D3 вносимо формулу
СУММПРОИЗВ($B$2;$C$2;B3;C3),
яку копіюємо в комірки D5, D6 і D7 з модифікаціями.
Для внесення в комірку D3 зазначених формул необхідно
1) поставити курсор у комірку D3;
2) викликати “Мастер функций” за допомогою кнопки  (див. рис. 1.2);
(див. рис. 1.2);
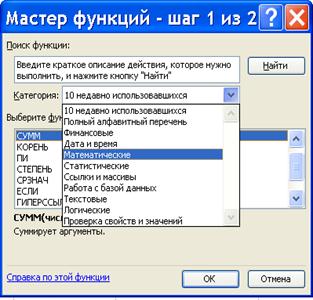
3) серед категорій майстра функцій вибрати «Математические» (рис. 1.3, а);
|
| а) б)
|
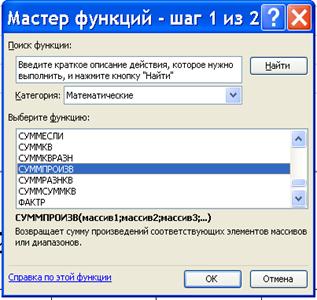
| Рис. 1.3 ‑ Екранна форма «Мастер функций»
|
4) серед вбудованих функцій цієї категорії відмітити
«СУММПРОИЗВ» (рис. 1.3, б) і натиснути «ОК»;
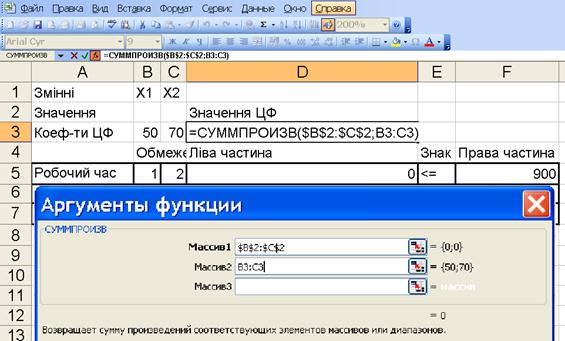
5) в екранній формі (див. рис. 1.4), що з'явилася, поставити курсор у «Массив 1», виділити на аркуші EXEL комірки В2:C2 (відповідають зарезервованим значенням змінних), потім привласнити їм абсолютні адреси натисканням функціональної клавіші F4; перевести курсор у «Массив 2» і виділити на аркуші EXEL комірки В3:С3 (відповідають значенням коефіцієнтів цільової функції).
|
| Рис. 1.4 ‑ Програмування цільової комірки
|
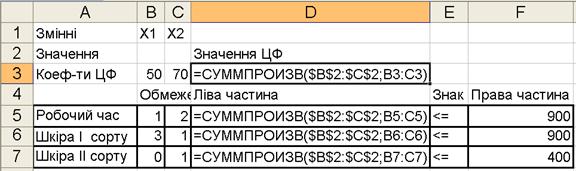
Після копіювання формул у комірки D5, D6 і D7 вони будуть модифіковані так, як показано на рис. 1.5.
|
| Рис. 1.5 ‑ Програмування комірок, що відповідають значенню цільової функції і значенням лівих частин системи обмежень
|
Якщо перелік процедур «Сервис» у меню Microsoft EXEL не містить інструмент «Поиск решения», то для додавання цього інструмента в перелік необхідно виконати такі дії:
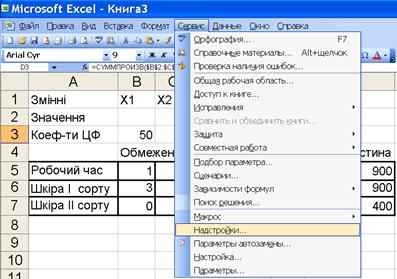
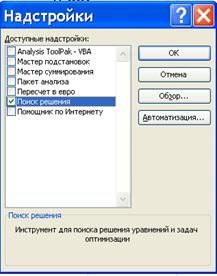
1) натиснути «Сервис», потім «Надстройки» (рис. 1.6 а);
2) в екранній формі, що з'явилася, відмітити «Поиск решения» (рис. 1.6, б).
|
| а) б)
Рис. 1.6 ‑ Додавання процедури «Поиск решения» в меню «Сервис» Microsoft EXEL
|
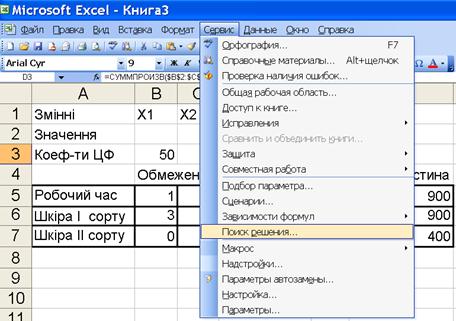
У результаті пророблених операцій аркуш EXEL готовий для запуску процедури «Поиск решения». Вибираємо в “Сервис” процедуру “Поиск решения” (див. рис. 1.7).
|
| Рис. 1.7 ‑ Запуск процедури «Поиск решения»
|
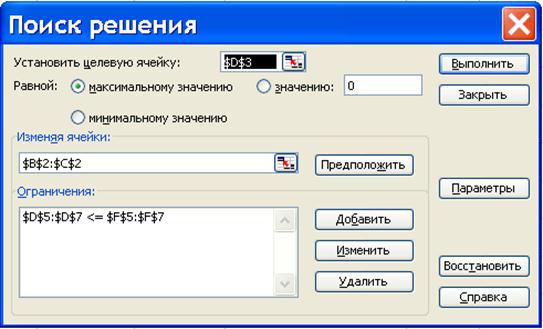
В екранній формі «Поиск решения» (див. рис 1.8)
1) установлюємо цільову комірку $D$3, відзначаючи її на аркуші EXEL;
2) відзначаємо прапорцем тип оптимізації, виходячи з умов задачі: у даному випадку – це максимізація;
3) переводимо курсор в «Изменяя ячейки» і виділяємо на аркуші EXEL комірки $В$2:$С$2, що відповідають зарезервованим значенням змінних;
4) переводимо курсор в «Ограничения», натискаємо «Добавить»;
|
| Рис. 1.8 ‑ Екранна форма «Поиск решения»
|
|
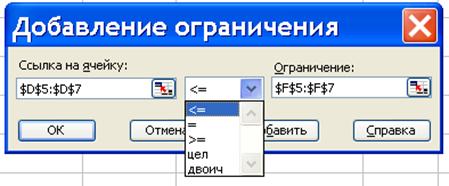
| Рис. 1.9 ‑ Екранна форма «Добавление ограничений»
|
|
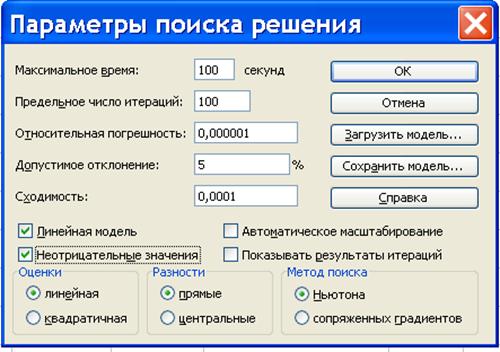
| Рис. 1.10 ‑ Екранна форма «Параментры поиска решений»
|
5) в екранній формі «Добавление ограничений» (рис. 1.9)
а) робимо посилання на комірки (шляхом їхнього виділення на аркуші EXEL), що відповідають лівим частинам системи обмежень $D$5:$D$7; ці комірки містять результат обчислень відповідно до введених раніше формул;
б) установлюємо знак, що відповідає знаку нерівності системи обмежень: у даному випадку це «<=»; якщо не всі обмеження мають однаковий знак, то, розташувавши поруч нерівності одного знака, програмують окремо кожну з груп, що утворилися;
в) переводимо курсор в «Ограничения», посилаючись на комірки, що відповідають правим частинам системи обмежень $F$5:$F$7, виділяючи їх на аркуші EXEL;
г) натискання «ОК» повертає нас в екранну форму «Поиск решения»;
6) натискаємо «Параметри», в екранній формі, що з'явилася, (рис. 1.10) відмічаємо прапорцями «Линейная модель» і «Неотрицательные значения», після чого натискання «ОК» повертає нас до екранної форми «Поиск решения»;
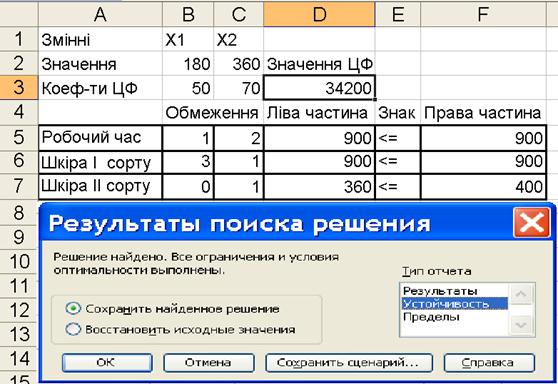
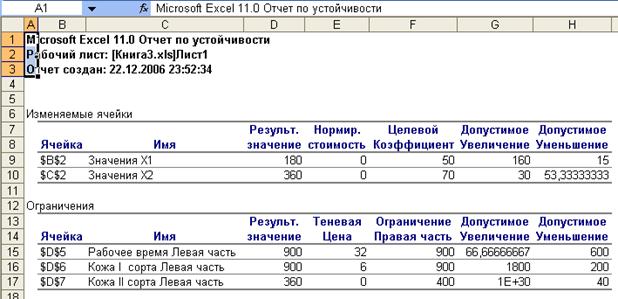
7) натискаємо «Выполнить», у результаті чого (рис. 1.11) на аркуші EXEL у комірках В2:С2 висвічуються шукані значення оптимальних змінних (оптимальний план), у комірці D3 ‑ значення цільової функції на оптимальному плані, а в екранній формі, що з'явилися, «Результаты поиска решения», пропонується зробити один з видів звіту, з яких вибираємо звіт по стійкості[2] і натискаємо «ОК». Аркуш «Отчет по устойчивости» представлений на рис. 1.12.
|
| Рис. 1.11 ‑ Результати роботи процедури «Поиск решения»
|
|
| Рис. 1.12 ‑ Екранна форма аркуша «Отчет по устойчивости»
|


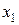 пар взуття – тижневий план випуску моделі №1,
пар взуття – тижневий план випуску моделі №1,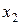 пар взуття – тижневий план випуску моделі №2.
пар взуття – тижневий план випуску моделі №2.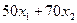 (грн.). Таким чином, цільова функція задачі, яку необхідно максимізувати, має вигляд
(грн.). Таким чином, цільова функція задачі, яку необхідно максимізувати, має вигляд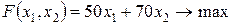 .
.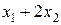 (люд.-год.). З урахуванням загального фонду робочого часу в 900 люд.-год., який не можна перевищити, одержимо нерівність:
(люд.-год.). З урахуванням загального фонду робочого часу в 900 люд.-год., який не можна перевищити, одержимо нерівність: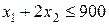 .
.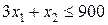 .
.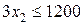 .
.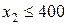 .
.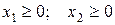 .
.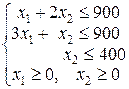
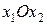 зобразимо множину точок
зобразимо множину точок 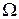 , координати яких задовольняють системі обмежень. Ця множина називається областю припустимих розв’язків (областю припустимих значень).
, координати яких задовольняють системі обмежень. Ця множина називається областю припустимих розв’язків (областю припустимих значень).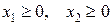 , які означають, що шукана область
, які означають, що шукана область 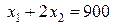 , (1)
, (1)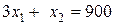 , (2)
, (2)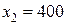 . (3)
. (3)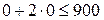 - вірно), то шукана півплощина містить цю точку; це зображено на рис. 1.1 за допомогою стрілок. Аналогічно, точка О(0,0) задовольняє кожній із нерівностей
- вірно), то шукана півплощина містить цю точку; це зображено на рис. 1.1 за допомогою стрілок. Аналогічно, точка О(0,0) задовольняє кожній із нерівностей 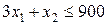 і
і 
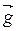 найшвидшого росту цільової функції
найшвидшого росту цільової функції 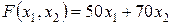 , яким є вектор, співспрямований її градієнту. Координатами вектора градієнта (для лінійної відносно змінних функції) є коефіцієнти при змінних цільової функції, тобто
, яким є вектор, співспрямований її градієнту. Координатами вектора градієнта (для лінійної відносно змінних функції) є коефіцієнти при змінних цільової функції, тобто 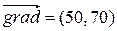 . Як вектор
. Як вектор 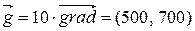 .
.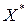 області
області 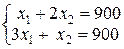 .
.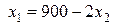 . (4)
. (4)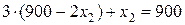 ,
,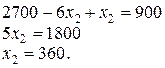
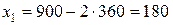 .
.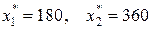 , а точка, яка відповідає оптимальному розв’язку, має координати
, а точка, яка відповідає оптимальному розв’язку, має координати 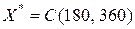 . Максимальне значення цільової функції:
. Максимальне значення цільової функції: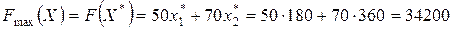 (грн.).
(грн.).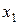 і
і 
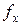 (див. рис. 1.2);
(див. рис. 1.2);










