Двійково-кодовані лічильники з довільним модулем – це лічильники з модулем, нерівним цілій степені числа 2. Для кожної конкретної задачі розроблюється своя схема, при цьому можливе використання декількох способів побудови:
1. модифікація міжрозрядних зв’язків;
2. керування скиданням.
Побудова лічильника першим способом
Побудова лічильника першим способом проілюструємо прикладом для М = 5, почавши з таблиці:
| Вихідний стан
| Наступний стан
| Функція збудження
|
| Q2
| Q1
| Q0
| Q2
| Q1
| Q0
| J2
| K2
| J1
| K1
| J0
| K0
|
|
|
|
|
|
|
|
X
| X
X
X
X
|
X
X
| X
X
X
|
X
X
| X
X
X
|
При знаходженні функції збудження тригерів використана таблиця істинності, яка враховує часовий фактор. Маючи на увазі, що замість символу довільного сигналу Х можна підставляти будь-яку змінну (0 або 1), з урахуванням таблиці запишемо: 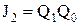 (у стовпці J2 залишена тільки одна одиниця),
(у стовпці J2 залишена тільки одна одиниця), 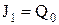 ,
, 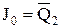 . Для функцій Ki (i = 0, 1, 2) виберемо варіанти з найбільшим числом констант, щоб менше навантажувати джерела сигналів.
. Для функцій Ki (i = 0, 1, 2) виберемо варіанти з найбільшим числом констант, щоб менше навантажувати джерела сигналів.
Приймемо, що K2 = 1, K1 = J1 та K0 = 1.
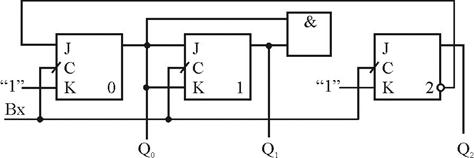
Рис.3.40. Схема лічильника з модулем 5
У спроектованій схемі лічильника зайві стани виключені у тому понятті, що вони не використовуються при нормальному функціонуванні лічильника. Але при збоях або після подачі на схему напруги живлення у початку її роботи зайві стани можуть виникати. Тому корисно визначити поведінку схеми (автомата), у котрій виник зайвий стан. Маючи схему, можна повністю передбачити поведінку схеми у всіх можливих ситуаціях. Зробимо це для схеми лічильника з модулем 5.
Взявши кожен зайвий стан, знайдемо для нього функції збудження тригерів, які визначають їх переходи у наступний стан. При необхідності знайдемо таким же способом наступний перехід і т.д. Для взятого прикладу зайвими є стани 101, 110 та 111.
У стані 101 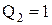 ,
, 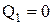 та
та 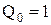 . Знаючи функції збудження тригерів, знаходимо, що
. Знаючи функції збудження тригерів, знаходимо, що 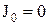 ,
, 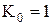 ,
, 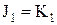 ,
, 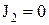 ,
, 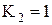 . Таким чином, тригери 0 і 2 скинуться, а тригер 1 перемкнеться у протилежний поточному стан та з зайвого стану 101 лічильник перейде у стан 010.
. Таким чином, тригери 0 і 2 скинуться, а тригер 1 перемкнеться у протилежний поточному стан та з зайвого стану 101 лічильник перейде у стан 010.
Аналогічним способом можна отримати результати для станів 100 та 111. У результаті зручно побудувати діаграму станів лічильника (граф переходів), в котрій врахований не тільки робочий цикл (його стани покажемо колами), але й поведінка автомата, що потрапив у невикористовуванні стани (ці стани показані прямокутниками). Така діаграма станів показана на рис.3.14. З діаграми видно, що лічильник, який розглядається, має властивість самозапуску (самовідновлення після збою) – незалежно від вихідного стану він приходить у робочий цикл після початку роботи. Ц властивість є не у всіх схем. У деяких схемах автоматичний вхід у робочий цикл не відбувається.
При розробці деяких схем у них вводять спеціальні елементи або підсхеми для придання властивостей самозапуску.
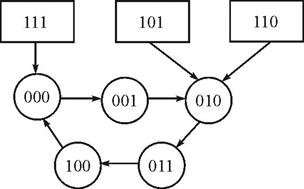
Рис.3.41. Діаграма станів лічильника з модулем 5
Серед лічильників з довільним модулем особливе місце займають двійково-десяткові, які мають модуль 10. У серіях ІС нерідко використовують ідентичні по іншим ознакам лічильники з модулями 16 та 10. Лічильник з модулем 10 неважко побудувати формально проілюстрованим вище методом.
Разом з секціонуванням двійково-десятковим лічильником у серіях ІС є і звичайні з різноманітними поєднаннями класифікаційних ознак (до 5…10 варіантів).


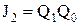 (у стовпці J2 залишена тільки одна одиниця),
(у стовпці J2 залишена тільки одна одиниця), 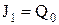 ,
, 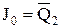 . Для функцій Ki (i = 0, 1, 2) виберемо варіанти з найбільшим числом констант, щоб менше навантажувати джерела сигналів.
. Для функцій Ki (i = 0, 1, 2) виберемо варіанти з найбільшим числом констант, щоб менше навантажувати джерела сигналів.
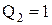 ,
, 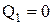 та
та 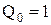 . Знаючи функції збудження тригерів, знаходимо, що
. Знаючи функції збудження тригерів, знаходимо, що 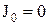 ,
, 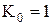 ,
, 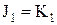 ,
, 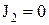 ,
, 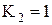 . Таким чином, тригери 0 і 2 скинуться, а тригер 1 перемкнеться у протилежний поточному стан та з зайвого стану 101 лічильник перейде у стан 010.
. Таким чином, тригери 0 і 2 скинуться, а тригер 1 перемкнеться у протилежний поточному стан та з зайвого стану 101 лічильник перейде у стан 010.