Рівняння балансу потужностей (4.14) в 4.3 було сформульоване для миттєвих значень. Воно виконується в кожний момент часу. У випадку періодичних полів розглядаються енергетичні співвідношення для середніх за період величин. Складемо рівняння балансу для середніх за період потужності гармонійного електромагнітного поля. Для цього знайдемо середнє за період значення величин, що входять в (4.14).
Середнє значення потужності електричного поля, можна отримати, використовуючи результат усереднення вигляду
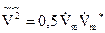 :
:
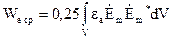 . (4.32)
. (4.32)
Середнє значення енергії магнітного поля, одержуємо аналогічно (4.32):
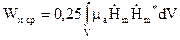 . (4.33)
. (4.33)
Середнє значення потужності можна отримати, використовуючи результат усереднення скалярного добутку
 ,
,
 , (4.34)
, (4.34)
де
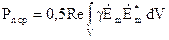 , (4.35)
, (4.35)
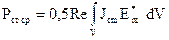 . (4.36)
. (4.36)
В (4.35) і (4.36) входять відповідно середні значення потужності джоулевих втрат і середні значення потужності сторонніх джерел.
Середнє значення потоку потужності можна отримати використовуючи усереднення векторного добутку
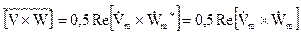 ,
,
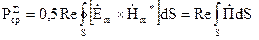 , (4.37)
, (4.37)
де 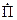 являється комплексним вектором Пойнтинга і дорівнює
являється комплексним вектором Пойнтинга і дорівнює
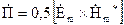 (4.38)
(4.38)
Тоді підінтегральний вираз лівого інтегралу в (4.37) являє собою середнє значення вектору Пойнтинга
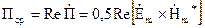 . (4.39)
. (4.39)
Для встановлення зв’язку між середніми величинами складемо, рівняння балансу для комплексної потужності. Скористуємось першим і другим рівнянням Максвела в комплексній формі, з урахуванням дії сторонніх джерел:
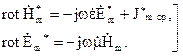 (4.40)
(4.40)
В (4.40) перше рівняння записане для комплексно-спряжених векторів, де 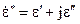 і
і 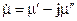 . Помноживши перше рівняння на
. Помноживши перше рівняння на 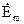 , а друге на
, а друге на  , далі виконуємо всі операції над (4.40) аналогічно, як це робилося при виведенні рівняння балансу для миттєвих значень (4.14) в 4.2. Виділивши в отриманому результаті дійсну і уявну частину отримаємо
, далі виконуємо всі операції над (4.40) аналогічно, як це робилося при виведенні рівняння балансу для миттєвих значень (4.14) в 4.2. Виділивши в отриманому результаті дійсну і уявну частину отримаємо
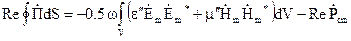 , (4.41)
, (4.41)
 . (4.42)
. (4.42)
Розглянемо фізичний зміст виразів (4.41) і (4.42). Найбільший інтерес представляє рівність (4.41). Тут:
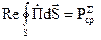 – середнє значення потоку потужності через S;
– середнє значення потоку потужності через S;
 – середнє значення потужності сторонніх джерел.
– середнє значення потужності сторонніх джерел.
Таким чином, вираз (4.41) записується
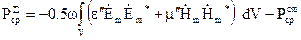 . (4.43)
. (4.43)
Отримана рівність характеризує середній баланс потужності при гармонійних коливаннях поля. Це рівняння має простий фізичний зміст. Якщо 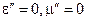 , то з (4.43) видно, що
, то з (4.43) видно, що 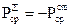 : потужність джерел, розташованих всередині V (
: потужність джерел, розташованих всередині V (  ), витрачається на випромінювання в зовнішній простір.
), витрачається на випромінювання в зовнішній простір.
Нехай тепер потік потужності через межу V в середньому дорівнює нулю:  . Тоді з (4.43) видно, що потужність сторонніх джерел витрачується всередині об’єму на нагрівання середовища в об’ємі V, тобто на втрати. Це можна записати
. Тоді з (4.43) видно, що потужність сторонніх джерел витрачується всередині об’єму на нагрівання середовища в об’ємі V, тобто на втрати. Це можна записати  , де
, де 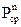 – потужність втрат в V. Отже інтеграл
– потужність втрат в V. Отже інтеграл
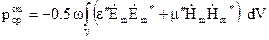 (4.44)
(4.44)
має зміст середнього значення потужності втрат в V.
Від’ємним значенням 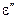 і
і 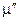 відповідає виділення енергії в середовищі (регенерація). Такі середовища називають активними. Тому (4.43) називають ще балансом активної потужності.
відповідає виділення енергії в середовищі (регенерація). Такі середовища називають активними. Тому (4.43) називають ще балансом активної потужності.
В рівності (4.43) величина.
 (4.45)
(4.45)
дорівнює амплітуді активної потужності сторонніх джерел.
Введемо поняття реактивної потужності в об’ємі V, тобто вияснимо фізичний зміст інтегралів в (4.42). При дійсних 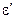 і
і  отримуємо
отримуємо
 , (4.46)
, (4.46)
де  – середнє значення енергії електричного поля;
– середнє значення енергії електричного поля;
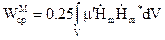 – середнє значення енергії магнітного поля.
– середнє значення енергії магнітного поля.
Величини 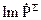 і
і 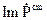 називають реактивним потоком енергії і реактивною потужністю сторонніх джерел. Ці величини змінюються в часі за гармонійним законом з частотою
називають реактивним потоком енергії і реактивною потужністю сторонніх джерел. Ці величини змінюються в часі за гармонійним законом з частотою 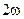 . Їх середнє за період значення дорівнює нулю. Це означає, що протягом періоду половину часу потужність має позитивне значення, а другу половину – від’ємне. Рівняння (4.46) являється рівнянням балансу реактивної потужності. Величина
. Їх середнє за період значення дорівнює нулю. Це означає, що протягом періоду половину часу потужність має позитивне значення, а другу половину – від’ємне. Рівняння (4.46) являється рівнянням балансу реактивної потужності. Величина
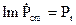 (4.47)
(4.47)
дорівнює амплітуді реактивної потужності сторонніх джерел.
Таким чином, в (4.46) реактивні величини зв’язані тут з різницею середніх значень електричної і магнітної енергії в V.
Якщо 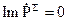 , то очевидно, (4.46) приймає вигляд:
, то очевидно, (4.46) приймає вигляд:
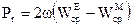 . (4.48)
. (4.48)
В цьому випадку в об'ємі V енергія електричного поля буде періодично перетворюватися в енергію магнітного поля і навпаки, при цьому 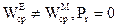 . Наявність реактивної потужності вказує на те, що при даних амплітудах
. Наявність реактивної потужності вказує на те, що при даних амплітудах  і
і 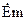 активна потужність не досягає свого максимуму.
активна потужність не досягає свого максимуму.
Якщо при деякій частоті 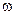 виявиться, що
виявиться, що 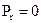 ,
, 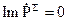 , то має місце резонанс, тобто
, то має місце резонанс, тобто 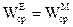 . Відношення
. Відношення
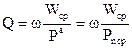 , (4.49)
, (4.49)
де  , називається добротністю ізольованої системи.
, називається добротністю ізольованої системи.


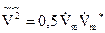 :
: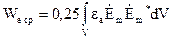 . (4.32)
. (4.32)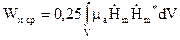 . (4.33)
. (4.33) ,
, , (4.34)
, (4.34)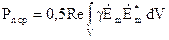 , (4.35)
, (4.35)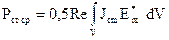 . (4.36)
. (4.36)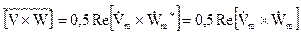 ,
,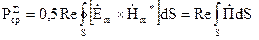 , (4.37)
, (4.37)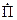 являється комплексним вектором Пойнтинга і дорівнює
являється комплексним вектором Пойнтинга і дорівнює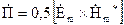 (4.38)
(4.38)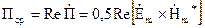 . (4.39)
. (4.39)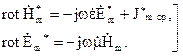 (4.40)
(4.40)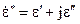 і
і 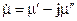 . Помноживши перше рівняння на
. Помноживши перше рівняння на 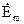 , а друге на
, а друге на  , далі виконуємо всі операції над (4.40) аналогічно, як це робилося при виведенні рівняння балансу для миттєвих значень (4.14) в 4.2. Виділивши в отриманому результаті дійсну і уявну частину отримаємо
, далі виконуємо всі операції над (4.40) аналогічно, як це робилося при виведенні рівняння балансу для миттєвих значень (4.14) в 4.2. Виділивши в отриманому результаті дійсну і уявну частину отримаємо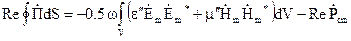 , (4.41)
, (4.41) . (4.42)
. (4.42)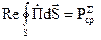 – середнє значення потоку потужності через S;
– середнє значення потоку потужності через S; – середнє значення потужності сторонніх джерел.
– середнє значення потужності сторонніх джерел.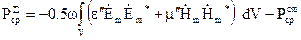 . (4.43)
. (4.43)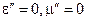 , то з (4.43) видно, що
, то з (4.43) видно, що 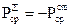 : потужність джерел, розташованих всередині V (
: потужність джерел, розташованих всередині V (  ), витрачається на випромінювання в зовнішній простір.
), витрачається на випромінювання в зовнішній простір. . Тоді з (4.43) видно, що потужність сторонніх джерел витрачується всередині об’єму на нагрівання середовища в об’ємі V, тобто на втрати. Це можна записати
. Тоді з (4.43) видно, що потужність сторонніх джерел витрачується всередині об’єму на нагрівання середовища в об’ємі V, тобто на втрати. Це можна записати  , де
, де 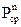 – потужність втрат в V. Отже інтеграл
– потужність втрат в V. Отже інтеграл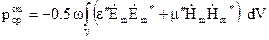 (4.44)
(4.44)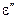 і
і 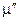 відповідає виділення енергії в середовищі (регенерація). Такі середовища називають активними. Тому (4.43) називають ще балансом активної потужності.
відповідає виділення енергії в середовищі (регенерація). Такі середовища називають активними. Тому (4.43) називають ще балансом активної потужності. (4.45)
(4.45)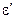 і
і  отримуємо
отримуємо , (4.46)
, (4.46) – середнє значення енергії електричного поля;
– середнє значення енергії електричного поля;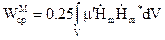 – середнє значення енергії магнітного поля.
– середнє значення енергії магнітного поля.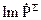 і
і 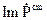 називають реактивним потоком енергії і реактивною потужністю сторонніх джерел. Ці величини змінюються в часі за гармонійним законом з частотою
називають реактивним потоком енергії і реактивною потужністю сторонніх джерел. Ці величини змінюються в часі за гармонійним законом з частотою 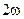 . Їх середнє за період значення дорівнює нулю. Це означає, що протягом періоду половину часу потужність має позитивне значення, а другу половину – від’ємне. Рівняння (4.46) являється рівнянням балансу реактивної потужності. Величина
. Їх середнє за період значення дорівнює нулю. Це означає, що протягом періоду половину часу потужність має позитивне значення, а другу половину – від’ємне. Рівняння (4.46) являється рівнянням балансу реактивної потужності. Величина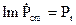 (4.47)
(4.47)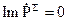 , то очевидно, (4.46) приймає вигляд:
, то очевидно, (4.46) приймає вигляд: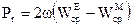 . (4.48)
. (4.48)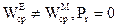 . Наявність реактивної потужності вказує на те, що при даних амплітудах
. Наявність реактивної потужності вказує на те, що при даних амплітудах  і
і  активна потужність не досягає свого максимуму.
активна потужність не досягає свого максимуму. виявиться, що
виявиться, що 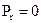 ,
, 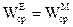 . Відношення
. Відношення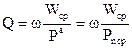 , (4.49)
, (4.49) , називається добротністю ізольованої системи.
, називається добротністю ізольованої системи.