Для отримання рівняння балансу необхідно скористатися першим і другим рівнянням Максвела в диференційній формі
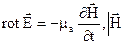 (4.9)
(4.9)
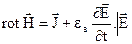 (4.10)
(4.10)
Помножимо (4.9) на вектор  , а (4.10) на вектор
, а (4.10) на вектор  , а після цього з (4.9) віднімемо з відповідних частин (4.10), отримаємо
, а після цього з (4.9) віднімемо з відповідних частин (4.10), отримаємо
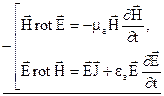
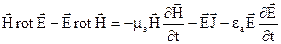 . (4.11)
. (4.11)
Використовуючи відому з векторного аналізу формулу
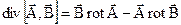 ,
,
згорнемо ліву частину (4.11)
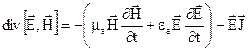 . (4.12)
. (4.12)
Проінтегрувавши (4.12) по об’єму V і застосувавши до лівої частини рівності (4.12) теорему Остроградського-Гауса
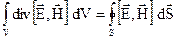 (4.13)
(4.13)
отримаємо остаточно
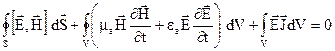 (4.14)
(4.14)
де 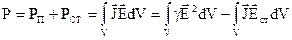 .
.
Рівність (4.14) являється рівнянням балансу енергії ЕМП. Розглянемо всі елементи цієї рівності і проаналізуємо їх. Звернемося до другого інтегралу в (4.14). Щоб з’ясувати фізичний зміст інтегралу
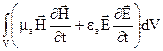 , (4.15)
, (4.15)
необхідно розглянути особливий випадок. Нехай всередині об’єму V до поверхні S примикає інша непроникна для поля оболонка S' (рис. 4.1). Тоді дотична складова 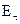 електричного поля буде дорівнювати нулю.
електричного поля буде дорівнювати нулю. 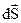 – елемент поверхні, яка співпадає із зовнішньою нормаллю
– елемент поверхні, яка співпадає із зовнішньою нормаллю 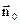 . Отже, поверхневий інтеграл в (4.14) буде дорівнювати нулю, через те, що нормальна компонента векторного добутку
. Отже, поверхневий інтеграл в (4.14) буде дорівнювати нулю, через те, що нормальна компонента векторного добутку  , визначається дотичними складовими векторів, які в нього входять.
, визначається дотичними складовими векторів, які в нього входять.
Значить, для ізольованої області рівняння балансу приймає вигляд
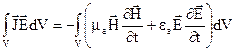 . (4.16)
. (4.16)
Інтеграл
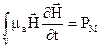 (4.17)
(4.17)
характеризує потужність магнітного поля, зосереджену в об’ємі V, або потужність, витрачену на утворення магнітного поля, а інтеграл
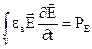 (4.18)
(4.18)
– потужність електричного поля, зосереджену в тому ж об’ємі.
Повну потужність електромагнітного поля в об’ємі V, можна представити для цього випадку як
 . (4.19)
. (4.19)
Отже, вираз (4.16) з урахуванням (4.19) приймає вигляд
 . (4.20)
. (4.20)
Якщо припустити, що середовище що заповнює об’єм V не володіє провідністю 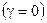 , тобто
, тобто  , то, очевидно, що потужність сторонніх джерел витрачається на зміну потужності
, то, очевидно, що потужність сторонніх джерел витрачається на зміну потужності 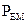 . Якщо втрати в об’ємі існують
. Якщо втрати в об’ємі існують 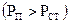 потужність
потужність 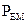 зменшується. Тому стоїть знак мінус. Якщо це не так, тобто
зменшується. Тому стоїть знак мінус. Якщо це не так, тобто 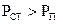 , то потужність поповнюється і всередині об’єму є генерація. Отже, всередині ізольованого об’єму можуть проходити тільки перетворення енергії з одного виду в інший.
, то потужність поповнюється і всередині об’єму є генерація. Отже, всередині ізольованого об’єму можуть проходити тільки перетворення енергії з одного виду в інший.
Розглянемо поверхневий інтеграл в (4.14)
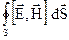 . (4.21)
. (4.21)
Підінтегральний вираз  являється вектором і вимірюється в
являється вектором і вимірюється в 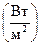 , як густина потоку потужності і носить назву вектора Пойнтинга
, як густина потоку потужності і носить назву вектора Пойнтинга
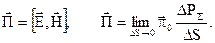 (4.22)
(4.22)
Напрямок вектора 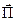 визначається по правилу векторного добутку, тобто він направлений перпендикулярно до площини, в якій розміщені вектори
визначається по правилу векторного добутку, тобто він направлений перпендикулярно до площини, в якій розміщені вектори  і
і  . Вектори
. Вектори  ,
,  і
і 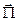 утворюють правогвинтову систему (рис. 4.2 а).
утворюють правогвинтову систему (рис. 4.2 а).
Модуль вектора 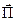 дорівнює
дорівнює
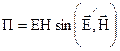 .
.
Вектор Пойнтинга чисельно дорівнює кількості потужності, яка проникає через одиничну площинку, розташовану перпендикулярно до напрямку розповсюдження потужності (рис. 4.2 в). Потік вектора Пойнтинга показує наскільки внутрішні процеси неврівноважені.
Від знаку інтеграла залежить напрямок потужності. При знакові “плюс” через поверхню потужність виходить з об’єму, розповсюджуючись за її межами (рис. 4.2 б). Це потужність випромінювання. При знакові “мінус” – потужність входить в об’єм, тобто буде поглинатися потужність зовнішнього випромінювання.

З урахуванням сказаного можна зробити висновок, що (4.21) характеризує потужність випромінювання і позначається
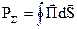 . (4.23)
. (4.23)
Процес обміну енергіями між виділеним об’ємом і навколишніми його областями простору називаєтьсявипромінюванням. Таким чином був розглянутий третій фактор зміни енергії електромагнітного поля, що згадується в 4.1.
Перепишемо рівняння балансу (4.14) з урахуванням (4.23) у вигляді
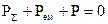 , (4.24)
, (4.24)
де  .
.
Потік вектору Пойнтинга можна проілюструвати за допомогою векторних ліній (за їх кількістю) і отримаємо різні варіанти балансу потужності (рис. 4.4)
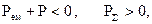 (4.25)
(4.25)
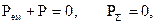 (4.26)
(4.26)
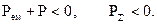 (4.27)
(4.27)
Якщо потік вектора Пойнтинга відрізняється від нуля – це означає, що існує контакт області V з навколишнім простором через межу S.
Умова (4.25) означає активний баланс, коли 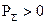 , при цьому
, при цьому 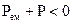 ; в рівнянні балансу (4.14) ця від’ємна величина врівноважується позитивним Пойнтингом (
; в рівнянні балансу (4.14) ця від’ємна величина врівноважується позитивним Пойнтингом (  ). Тобто зменшення запасу потужності в V, так і генерація викликають перехід потужності через межу S в зовнішнє середовище, тобто випромінювання. В найпростішому варіанті
). Тобто зменшення запасу потужності в V, так і генерація викликають перехід потужності через межу S в зовнішнє середовище, тобто випромінювання. В найпростішому варіанті 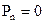 ,
, 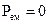 (запас потужності
(запас потужності

електромагнітного поля постійний), тоді згідно з (4.14)  , випромінювання створюється сторонніми джерелами.
, випромінювання створюється сторонніми джерелами.
Умова (4.26) означає нейтральний баланс, коли 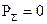 , при цьому
, при цьому 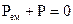 (рис. 4.3). Потік потужності може проходити наскрізь, так що число ліній вектора
(рис. 4.3). Потік потужності може проходити наскрізь, так що число ліній вектора 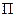 , що входять дорівнює числу що виходять; він може не входити в V, або зовсім бути відсутнім.Умова (4.27) означає пасивний баланс, коли
, що входять дорівнює числу що виходять; він може не входити в V, або зовсім бути відсутнім.Умова (4.27) означає пасивний баланс, коли 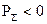 , при цьому
, при цьому 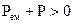 , тобто поглинання переважає над випромінюванням. Це означає, що внутрішні втрати
, тобто поглинання переважає над випромінюванням. Це означає, що внутрішні втрати  , або витрати на збільшення потужності електромагнітного поля
, або витрати на збільшення потужності електромагнітного поля 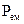 покриваються притоком енергії ззовні. Якщо
покриваються притоком енергії ззовні. Якщо 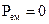 ,
, 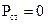 , то
, то 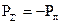 . Якщо
. Якщо 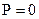 , то
, то  : поглинання зовнішнього випромінювання йде на збільшення запасу потужності електромагнітного поля.
: поглинання зовнішнього випромінювання йде на збільшення запасу потужності електромагнітного поля.


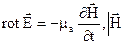 (4.9)
(4.9)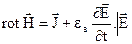 (4.10)
(4.10) , а (4.10) на вектор
, а (4.10) на вектор  , а після цього з (4.9) віднімемо з відповідних частин (4.10), отримаємо
, а після цього з (4.9) віднімемо з відповідних частин (4.10), отримаємо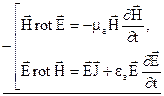
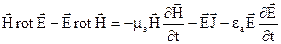 . (4.11)
. (4.11)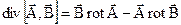 ,
,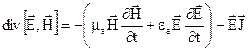 . (4.12)
. (4.12)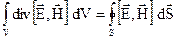 (4.13)
(4.13)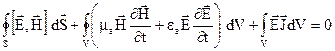 (4.14)
(4.14)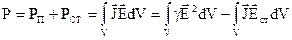 .
.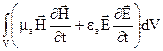 , (4.15)
, (4.15)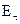 електричного поля буде дорівнювати нулю.
електричного поля буде дорівнювати нулю. 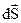 – елемент поверхні, яка співпадає із зовнішньою нормаллю
– елемент поверхні, яка співпадає із зовнішньою нормаллю 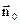 . Отже, поверхневий інтеграл в (4.14) буде дорівнювати нулю, через те, що нормальна компонента векторного добутку
. Отже, поверхневий інтеграл в (4.14) буде дорівнювати нулю, через те, що нормальна компонента векторного добутку  , визначається дотичними складовими векторів, які в нього входять.
, визначається дотичними складовими векторів, які в нього входять.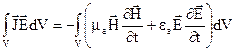 . (4.16)
. (4.16)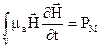 (4.17)
(4.17)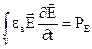 (4.18)
(4.18) . (4.19)
. (4.19) . (4.20)
. (4.20)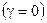 , тобто
, тобто  , то, очевидно, що потужність сторонніх джерел витрачається на зміну потужності
, то, очевидно, що потужність сторонніх джерел витрачається на зміну потужності 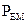 . Якщо втрати в об’ємі існують
. Якщо втрати в об’ємі існують 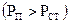 потужність
потужність 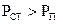 , то потужність поповнюється і всередині об’єму є генерація. Отже, всередині ізольованого об’єму можуть проходити тільки перетворення енергії з одного виду в інший.
, то потужність поповнюється і всередині об’єму є генерація. Отже, всередині ізольованого об’єму можуть проходити тільки перетворення енергії з одного виду в інший.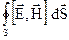 . (4.21)
. (4.21)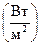 , як густина потоку потужності і носить назву вектора Пойнтинга
, як густина потоку потужності і носить назву вектора Пойнтинга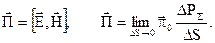 (4.22)
(4.22)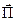 визначається по правилу векторного добутку, тобто він направлений перпендикулярно до площини, в якій розміщені вектори
визначається по правилу векторного добутку, тобто він направлений перпендикулярно до площини, в якій розміщені вектори 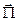 утворюють правогвинтову систему (рис. 4.2 а).
утворюють правогвинтову систему (рис. 4.2 а).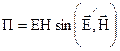 .
.
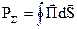 . (4.23)
. (4.23)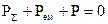 , (4.24)
, (4.24) .
.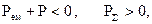 (4.25)
(4.25)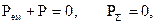 (4.26)
(4.26)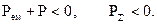 (4.27)
(4.27)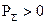 , при цьому
, при цьому 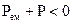 ; в рівнянні балансу (4.14) ця від’ємна величина врівноважується позитивним Пойнтингом (
; в рівнянні балансу (4.14) ця від’ємна величина врівноважується позитивним Пойнтингом (  ). Тобто зменшення запасу потужності в V, так і генерація викликають перехід потужності через межу S в зовнішнє середовище, тобто випромінювання. В найпростішому варіанті
). Тобто зменшення запасу потужності в V, так і генерація викликають перехід потужності через межу S в зовнішнє середовище, тобто випромінювання. В найпростішому варіанті 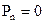 ,
, 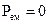 (запас потужності
(запас потужності
 , випромінювання створюється сторонніми джерелами.
, випромінювання створюється сторонніми джерелами.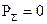 , при цьому
, при цьому 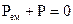 (рис. 4.3). Потік потужності може проходити наскрізь, так що число ліній вектора
(рис. 4.3). Потік потужності може проходити наскрізь, так що число ліній вектора 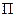 , що входять дорівнює числу що виходять; він може не входити в V, або зовсім бути відсутнім.Умова (4.27) означає пасивний баланс, коли
, що входять дорівнює числу що виходять; він може не входити в V, або зовсім бути відсутнім.Умова (4.27) означає пасивний баланс, коли 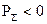 , при цьому
, при цьому 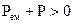 , тобто поглинання переважає над випромінюванням. Це означає, що внутрішні втрати
, тобто поглинання переважає над випромінюванням. Це означає, що внутрішні втрати  , або витрати на збільшення потужності електромагнітного поля
, або витрати на збільшення потужності електромагнітного поля 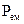 покриваються притоком енергії ззовні. Якщо
покриваються притоком енергії ззовні. Якщо 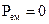 ,
, 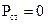 , то
, то 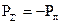 . Якщо
. Якщо 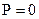 , то
, то  : поглинання зовнішнього випромінювання йде на збільшення запасу потужності електромагнітного поля.
: поглинання зовнішнього випромінювання йде на збільшення запасу потужності електромагнітного поля.