Електромагнітне поле володіє енергією. Ця енергія може перетворюватися в інші види енергії. З’ясуємо яким чином вектори поля  ,
, 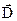 ,
,  ,
, 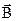 визначають енергію електромагнітного поля.
визначають енергію електромагнітного поля.
Таблиця 4.1 - Енергетичні величини в теорії електромагнетизму
| Назва
| Позначення
| Од. вимірювання (Сі)
|
| 1. Енергія електромагнітного поля
| 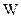
| Джоуль (Дж)
|
| 2. Електрична енергія
| 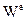
| Джоуль (Дж)
|
| 3. Магнітна енергія
| 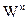
| Джоуль (Дж)
|
| 4. Потужність
| 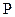
| Ватт (Вт)
|
| 5. Потужність поглинання (потужність втрат)
| 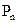
| Ватт (Вт)
|
| 6. Потужність сторонніх джерел (потужність джерел)
| 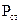
| Ватт (Вт)
|
| 7. Густина енергії електромагнітного поля
| 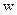
| 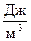
|
| 8. Густина електричної енергії
| 
| 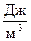
|
| 9. Густина магнітної енергії
| 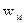
| 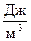
|
| 10. Густина потужності
| 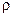
| 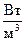
|
| 11. Густина потужності поглинання
| 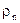
| 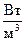
|
| 12. Густина потужності сторонніх джерел
| 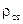
| 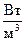
|
| 13. Потік потужності
| 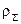
| Вт
|
| 14. Густина потоку потужності
| 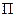
| 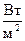
|
Енергія електромагнітного поля ЕЕМП, яка знаходиться всередині об’єму V змінюється. Факторами зміни енергії являються:
а) перетворення частини ЕЕМП в інші види енергії;
б) робота сторонніх джерел, що можуть як збільшувати запас енергії, так і зменшувати його;
в) обмін енергії між виділеним об’ємом V і навколишніми його областями простору за рахунок процесу, який називається випромінюванням.
Розглянемо перший фактор. З фізики відомо, що при наявності струму в середовищі виділяється тепло. За законом Джоуля-Лєнца можна записати
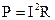 .
.
Він визначає потужність джоулевих втрат. Застосовуючи цю формулу до нескінченного малого циліндра об’ємом 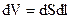 , отримаємо
, отримаємо
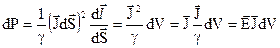 .
.
Інтегруючи цей вираз, отримаємо
 . (4.1)
. (4.1)
Підінтегральний вираз
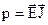
являється густиною потужності, тобто потужність віднесена до одиниці об’єму
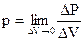 . (4.2)
. (4.2)
Отриманий вираз потужності (4.1) і її густини (4.2) мають універсальний характер. Вони справедливі не тільки при розрахунку джоулевих втрат, але і в усіх випадках, коли розглядаються струми.
В залежності від напрямку руху зарядів величина густини потужності 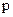 може бути як позитивної так і негативної. Заряди можуть прискорюватися полем. При цьому
може бути як позитивної так і негативної. Заряди можуть прискорюватися полем. При цьому 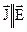 ,
,  і енергія у поля відбирається. Очевидно, що
і енергія у поля відбирається. Очевидно, що  , якщо
, якщо 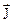 і
і  антипаралельні. Це в тому випадку, якщо рух зарядів проти поля створюється якимось не електромагнітним “стороннім” процесом, який віддає свою енергію полю, яке гальмує заряди.
антипаралельні. Це в тому випадку, якщо рух зарядів проти поля створюється якимось не електромагнітним “стороннім” процесом, який віддає свою енергію полю, яке гальмує заряди.
Розглянемо другий фактор. Дії сторонніх джерел змінюють матеріальне рівняння – закон Ома в диференційній формі 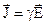 :
:
 . (4.3)
. (4.3)
Визначимо, використовуючи (4.3), напруженість електричного поля  . Поділивши цей вираз на
. Поділивши цей вираз на 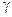 – питому провідність, отримаємо:
– питому провідність, отримаємо:
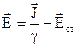 . (4.4)
. (4.4)
Помноживши праву і ліву частину (4.4) на 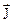 – об’ємну густину струму провідності, отримаємо густину потужності р:
– об’ємну густину струму провідності, отримаємо густину потужності р:
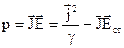 . (4.5)
. (4.5)
Рівність (4.5) можна записати у вигляді
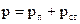 , (4.6)
, (4.6)
де
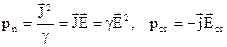 . (4.7)
. (4.7)
Густина потужності втрат 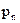 в (4.7) характеризує поглинання, втрати електромагнітного процесу (перетворення в тепло, джоулева потужність). Критерій придатності:
в (4.7) характеризує поглинання, втрати електромагнітного процесу (перетворення в тепло, джоулева потужність). Критерій придатності: 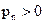 (поле віддає енергію), якщо кут між
(поле віддає енергію), якщо кут між 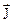 і
і  менше
менше 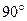 .
.
Густина сторонніх джерел характеризує процес перетворення енергії різних видів (наприклад, хімічної, механічної) в електромагнітну. Критерій придатності: 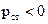 (поле набуває енергії), якщо кут між
(поле набуває енергії), якщо кут між 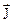 і
і 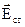 більше
більше 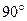 (скалярний добуток менший нуля). Виникають так звані “негативні втрати”. Найбільш ефективне віддання енергії ЕМП від сторонніх джерел, коли
(скалярний добуток менший нуля). Виникають так звані “негативні втрати”. Найбільш ефективне віддання енергії ЕМП від сторонніх джерел, коли 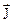 і
і 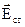 протилежно направлені.
протилежно направлені.
Сторонні сили, як правило локалізовані. Якщо, наприклад, вони зосередженні в деякій області  то згідно рівності (4.3)
то згідно рівності (4.3) 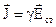 в
в  і
і 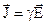 поза
поза  . Область
. Область  – називається областю джерела сторонніх сил. Проінтегрувавши по об’єму V вираз (4.7), отримаємо повну потужність
– називається областю джерела сторонніх сил. Проінтегрувавши по об’єму V вираз (4.7), отримаємо повну потужність
 .
.
Цю рівність можна записати у вигляді 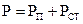 , де
, де
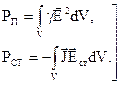 (4.8)
(4.8)
Третій фактор буде розглянутий в п. 4.2.


 ,
, 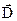 ,
,  ,
, 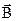 визначають енергію електромагнітного поля.
визначають енергію електромагнітного поля.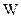
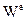
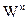
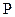
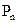
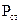
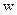
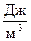

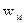
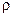
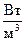
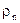
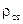
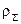
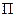
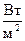
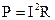 .
.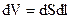 , отримаємо
, отримаємо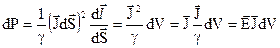 .
. . (4.1)
. (4.1)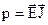
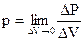 . (4.2)
. (4.2)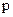 може бути як позитивної так і негативної. Заряди можуть прискорюватися полем. При цьому
може бути як позитивної так і негативної. Заряди можуть прискорюватися полем. При цьому 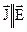 ,
,  і енергія у поля відбирається. Очевидно, що
і енергія у поля відбирається. Очевидно, що  , якщо
, якщо 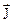 і
і 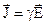 :
: . (4.3)
. (4.3)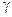 – питому провідність, отримаємо:
– питому провідність, отримаємо: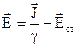 . (4.4)
. (4.4)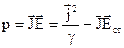 . (4.5)
. (4.5)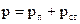 , (4.6)
, (4.6)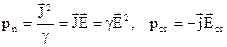 . (4.7)
. (4.7)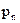 в (4.7) характеризує поглинання, втрати електромагнітного процесу (перетворення в тепло, джоулева потужність). Критерій придатності:
в (4.7) характеризує поглинання, втрати електромагнітного процесу (перетворення в тепло, джоулева потужність). Критерій придатності: 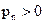 (поле віддає енергію), якщо кут між
(поле віддає енергію), якщо кут між 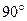 .
.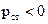 (поле набуває енергії), якщо кут між
(поле набуває енергії), якщо кут між 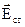 більше
більше  то згідно рівності (4.3)
то згідно рівності (4.3) 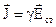 в
в 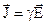 поза
поза  .
.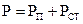 , де
, де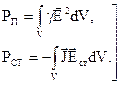 (4.8)
(4.8)