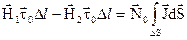 , (3.22)
, (3.22)
де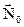 – орт до додаткової поверхні Р.
– орт до додаткової поверхні Р.
Розглянемо інтеграл в правій частині (3.22). Вектор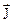 в ньому являється вектором об'ємної густини струму провідності, який визначається співвідношенням
в ньому являється вектором об'ємної густини струму провідності, який визначається співвідношенням
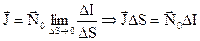 . (3.23)
. (3.23)
При 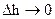 , струми будуть розподілені по поверхні у вигляді тонкого шару. Такі струми називаються поверхневими (рис. 3.6). Густина поверхневих струмів визначається співвідношенням
, струми будуть розподілені по поверхні у вигляді тонкого шару. Такі струми називаються поверхневими (рис. 3.6). Густина поверхневих струмів визначається співвідношенням
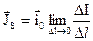 ,
,
де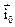 – одиничний вектор, який вказує напрямок руху зарядів в даній точці.
– одиничний вектор, який вказує напрямок руху зарядів в даній точці.
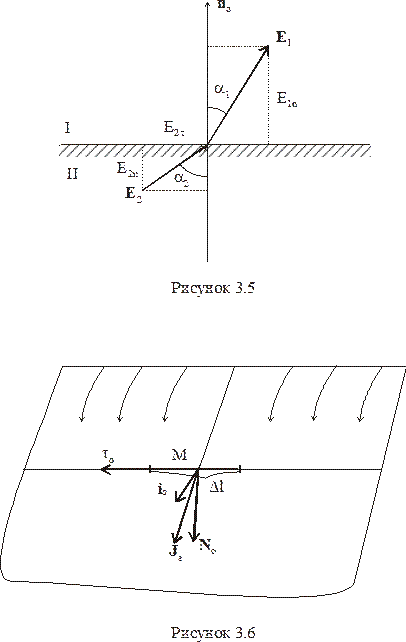
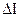 – перетинаючий струмом відрізок лінії, перпендикулярний вектору
– перетинаючий струмом відрізок лінії, перпендикулярний вектору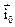 .
.
Звідки
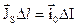 . (3.24)
. (3.24)
З рисунку 3.4 видно, що найбільшу величину зміни дотична складова 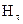 буде мати в напрямку перпендикулярному до вектору густини поверхневого струму, тобто при співпаданні одиничних векторів
буде мати в напрямку перпендикулярному до вектору густини поверхневого струму, тобто при співпаданні одиничних векторів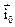 і
і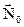 .
.
Тоді з урахуванням цього зауваження (3.24) можна записати 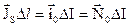 . (3.25)
. (3.25)
Вважаючи розподілення густини поверхневого струму на відрізку 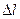 рівномірним і використовуючи (3.23) і (3.24), перетворимо праву частину рівності (3.22) наступним чином:
рівномірним і використовуючи (3.23) і (3.24), перетворимо праву частину рівності (3.22) наступним чином:
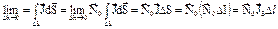 . (3.26)Підставивши (3.26) в (3.22) і скоротивши на спільний множник
. (3.26)Підставивши (3.26) в (3.22) і скоротивши на спільний множник 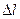 , отримаємо
, отримаємо
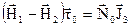 , або
, або 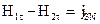 ,
,
де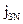 – проекція
– проекція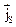 на напрямок
на напрямок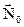 .
.
Щоб отримати співвідношення (3.20) необхідно замінити 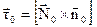 і скористатися властивістю змішаного добутку векторів. В результаті маємо
і скористатися властивістю змішаного добутку векторів. В результаті маємо
 ,
,
Через те, що орт  , який задає орієнтацію площини Р, являється невизначеним, то це співвідношення має кінцевий вигляд що повністю співпадає з (3.20)
, який задає орієнтацію площини Р, являється невизначеним, то це співвідношення має кінцевий вигляд що повністю співпадає з (3.20)
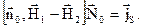
Дотичні складові вектору магнітної індукції будуть розривні на межі розділу
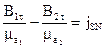 . (3.27)
. (3.27)


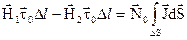 , (3.22)
, (3.22)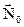 – орт до додаткової поверхні Р.
– орт до додаткової поверхні Р.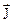 в ньому являється вектором об'ємної густини струму провідності, який визначається співвідношенням
в ньому являється вектором об'ємної густини струму провідності, який визначається співвідношенням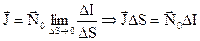 . (3.23)
. (3.23)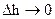 , струми будуть розподілені по поверхні у вигляді тонкого шару. Такі струми називаються поверхневими (рис. 3.6). Густина поверхневих струмів визначається співвідношенням
, струми будуть розподілені по поверхні у вигляді тонкого шару. Такі струми називаються поверхневими (рис. 3.6). Густина поверхневих струмів визначається співвідношенням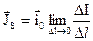 ,
,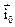 – одиничний вектор, який вказує напрямок руху зарядів в даній точці.
– одиничний вектор, який вказує напрямок руху зарядів в даній точці.
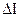 – перетинаючий струмом відрізок лінії, перпендикулярний вектору
– перетинаючий струмом відрізок лінії, перпендикулярний вектору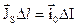 . (3.24)
. (3.24)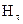 буде мати в напрямку перпендикулярному до вектору густини поверхневого струму, тобто при співпаданні одиничних векторів
буде мати в напрямку перпендикулярному до вектору густини поверхневого струму, тобто при співпаданні одиничних векторів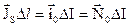 . (3.25)
. (3.25)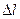 рівномірним і використовуючи (3.23) і (3.24), перетворимо праву частину рівності (3.22) наступним чином:
рівномірним і використовуючи (3.23) і (3.24), перетворимо праву частину рівності (3.22) наступним чином: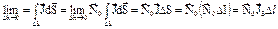 . (3.26)Підставивши (3.26) в (3.22) і скоротивши на спільний множник
. (3.26)Підставивши (3.26) в (3.22) і скоротивши на спільний множник 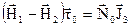 , або
, або 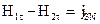 ,
,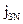 – проекція
– проекція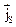 на напрямок
на напрямок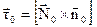 і скористатися властивістю змішаного добутку векторів. В результаті маємо
і скористатися властивістю змішаного добутку векторів. В результаті маємо ,
, , який задає орієнтацію площини Р, являється невизначеним, то це співвідношення має кінцевий вигляд що повністю співпадає з (3.20)
, який задає орієнтацію площини Р, являється невизначеним, то це співвідношення має кінцевий вигляд що повністю співпадає з (3.20)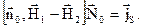
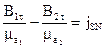 . (3.27)
. (3.27)