
Мови програмуванняВідео уроки php mysqlПаскальСіАсемблерJavaMatlabPhpHtmlJavaScriptCSSC#DelphiТурбо Пролог1С Компьютерные сетиСистемное программное обеспечениеИнформационные технологииПрограммирование Linux
Unix
Алгоритмічні мови
Архітектура мікроконтролерів
Введення в розробку розподілених інформаційних систем
Дискретна математика
Інформаційне обслуговування користувачів
Інформація та моделювання в управлінні виробництвом
Комп'ютерна графіка
Лекції
|
Закон Ома в диференційній форміДата додавання: 2014-10-07; переглядів: 1423.
|
Онлайн система числення Калькулятор онлайн звичайний Науковий калькулятор онлайн
| ||||||||||||||||

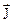 в який-небудь точці провідного середовища від напруженості електричного поля
в який-небудь точці провідного середовища від напруженості електричного поля  в цій точці. Перехід від звичайного закону Ома до диференційної форми можна зробити таким чином. В провіднику виділяється достатньо малий циліндр довжиною
в цій точці. Перехід від звичайного закону Ома до диференційної форми можна зробити таким чином. В провіднику виділяється достатньо малий циліндр довжиною 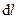 і поперечним перерізом
і поперечним перерізом 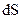 . Вектор
. Вектор 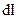 уздовж осі циліндра дорівнює
уздовж осі циліндра дорівнює . (2.38)
. (2.38) визначається із геометрії циліндра і через питому провідність
визначається із геометрії циліндра і через питому провідність 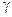 речовини провідника, по формулі, відомої з фізики
речовини провідника, по формулі, відомої з фізики
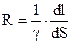 , (2.39)
, (2.39) – довжина твірної циліндра.
– довжина твірної циліндра.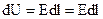 . (2.40)
. (2.40) .
.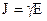 ,
,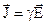 . (2.41)
. (2.41)