Розглянемо деякі задачі аналітичної геометрії, пов'язані з взаємним розташуванням точок на площині або в просторі.
Ділення відрізка в заданому відношенні. Завдання полягає в тому, щоб на даному відрізку  знайти точку М, яка ділить відрізок у заданому відношенні:
знайти точку М, яка ділить відрізок у заданому відношенні: 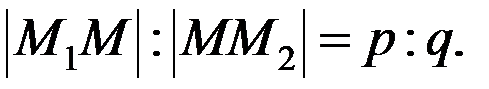
Для точки М з відрізка 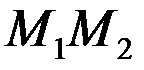 вектори
вектори 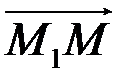 і
і 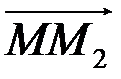 колінеарні і однаково напрямлені (рис. 5.7). Отже, один з них може бути отриманий з іншого множенням на додатне число. Нехай
колінеарні і однаково напрямлені (рис. 5.7). Отже, один з них може бути отриманий з іншого множенням на додатне число. Нехай 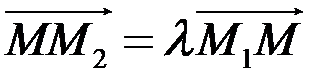 . Число
. Число 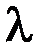 дорівнює відношенню довжин відрізків
дорівнює відношенню довжин відрізків 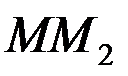 та
та 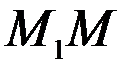 , тобто
, тобто 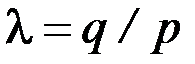 Тому
Тому 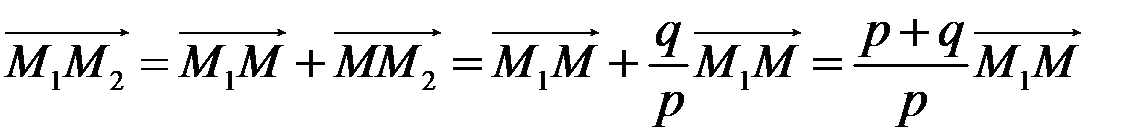 ,
,
звідки 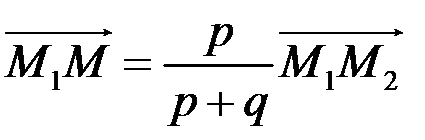 .
.
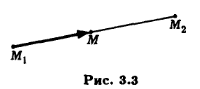
Рис. 5.7.
Нехай кінці 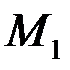 і
і 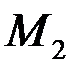 відрізка задані своїми координатами в довільній прямокутній системі координат
відрізка задані своїми координатами в довільній прямокутній системі координат 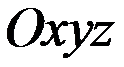 в просторі:
в просторі: 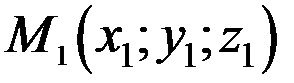 ,
,
 . Знайдемо координати точки М в цій системі координат:
. Знайдемо координати точки М в цій системі координат:
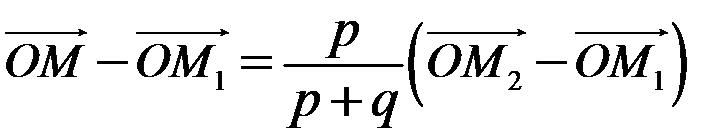
і знайдемо, що
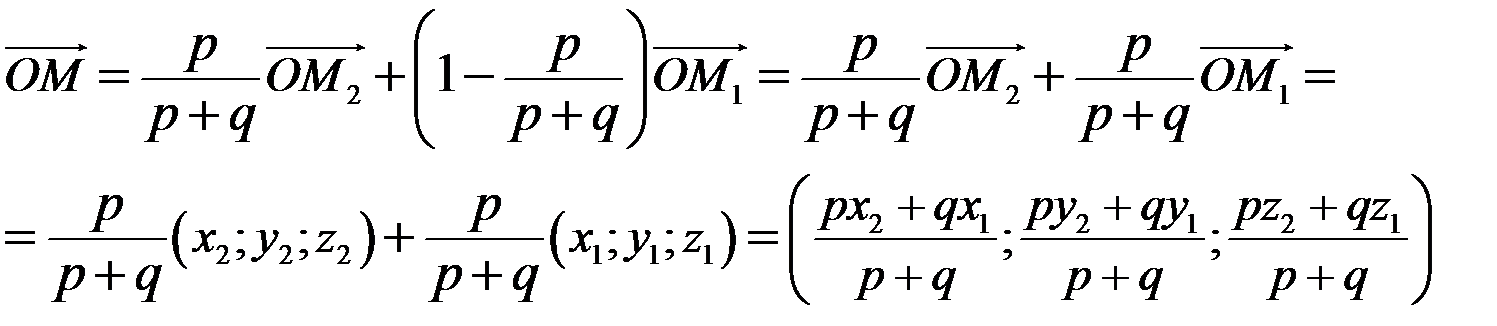
Отже, якщо позначити координати точки М через 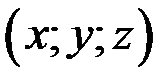 , то
, то
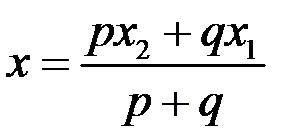 ,
, 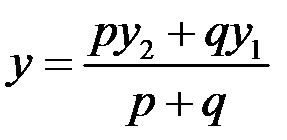 ,
, 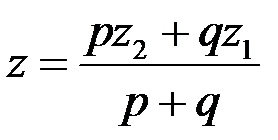 (5.1)
(5.1)
Якщо точка М - середина відрізка 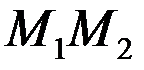 , то
, то 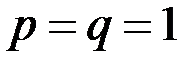 , і тому з (5.1) випливає, що координати М рівні напівсумі відповідних координат початку і кінця відрізка, тобто
, і тому з (5.1) випливає, що координати М рівні напівсумі відповідних координат початку і кінця відрізка, тобто
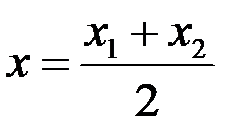 ,
,  ,
, 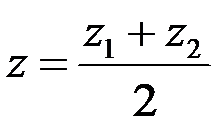 (5.2)
(5.2)
На площині 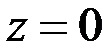 і координати точки М (х; у), що ділить відрізок
і координати точки М (х; у), що ділить відрізок  у заданому відношенні визначаються через координати точок
у заданому відношенні визначаються через координати точок 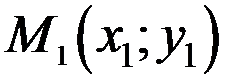 і
і  кінців цього відрізка за допомогою рівностей
кінців цього відрізка за допомогою рівностей
 ,
, 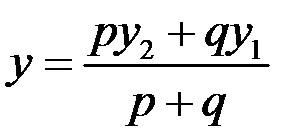 ,
,
які для середини відрізка переходять в співвідношення
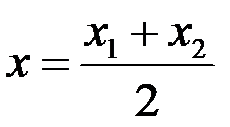 ,
, 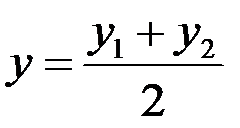 .
.
Приклад 5.9. В вершинах А(4, 4, 4), В(-2; 6, 4), С(-4; 4, 2) трикутника АВС розташовані матеріальні точки рівної маси. Знайти координати центру мас цієї системи точок.
Розв’язання. Центр мас зазначеної системи точок співпадає з точкою М перетину медіан трикутника АВС. Нехай точка N - середина сторони ВС. Тоді її координати 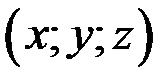 рівні напівсумі відповідних координат точок В і С, отже, х = -3, у = 5, z = 3.Медіану AN точка М ділить у відношенні
рівні напівсумі відповідних координат точок В і С, отже, х = -3, у = 5, z = 3.Медіану AN точка М ділить у відношенні 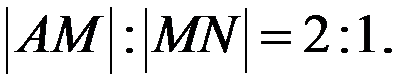 , тому координати
, тому координати 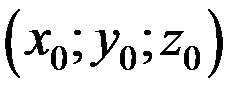 центру мас розглянутого трикутника рівні:
центру мас розглянутого трикутника рівні:
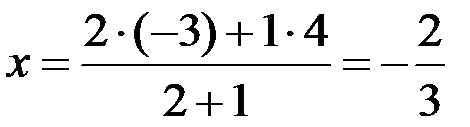 ,
, 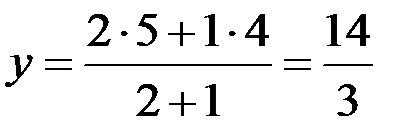 ,
, 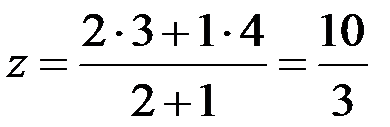 .
.
Відповідь:  .
.


 знайти точку М, яка ділить відрізок у заданому відношенні:
знайти точку М, яка ділить відрізок у заданому відношенні: 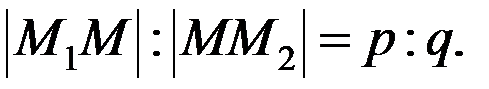
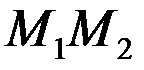 вектори
вектори 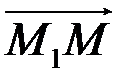 і
і 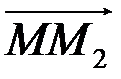 колінеарні і однаково напрямлені (рис. 5.7). Отже, один з них може бути отриманий з іншого множенням на додатне число. Нехай
колінеарні і однаково напрямлені (рис. 5.7). Отже, один з них може бути отриманий з іншого множенням на додатне число. Нехай 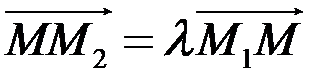 . Число
. Число 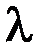 дорівнює відношенню довжин відрізків
дорівнює відношенню довжин відрізків 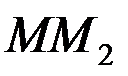 та
та 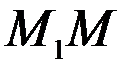 , тобто
, тобто 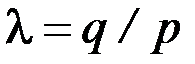 Тому
Тому 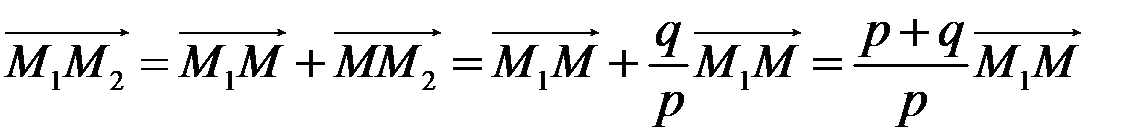 ,
,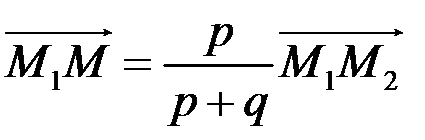 .
.
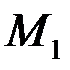 і
і 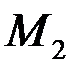 відрізка задані своїми координатами в довільній прямокутній системі координат
відрізка задані своїми координатами в довільній прямокутній системі координат 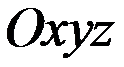 в просторі:
в просторі: 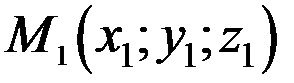 ,
, . Знайдемо координати точки М в цій системі координат:
. Знайдемо координати точки М в цій системі координат: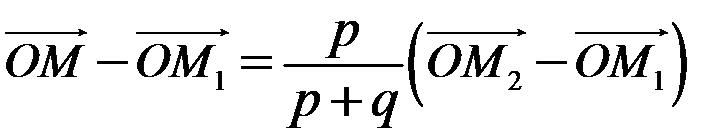
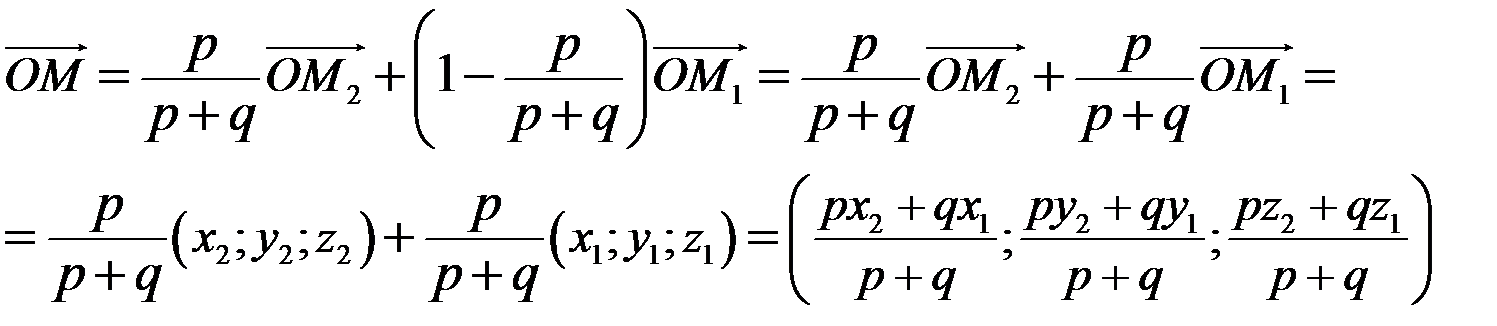
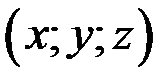 , то
, то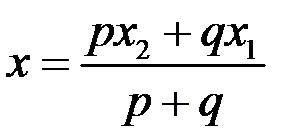 ,
, 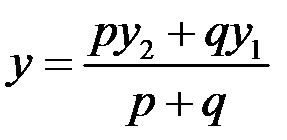 ,
, 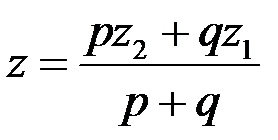 (5.1)
(5.1)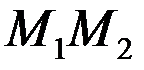 , то
, то 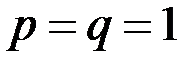 , і тому з (5.1) випливає, що координати М рівні напівсумі відповідних координат початку і кінця відрізка, тобто
, і тому з (5.1) випливає, що координати М рівні напівсумі відповідних координат початку і кінця відрізка, тобто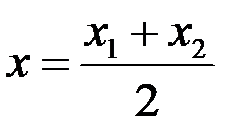 ,
,  ,
, 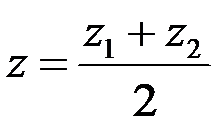 (5.2)
(5.2)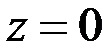 і координати точки М (х; у), що ділить відрізок
і координати точки М (х; у), що ділить відрізок  у заданому відношенні визначаються через координати точок
у заданому відношенні визначаються через координати точок 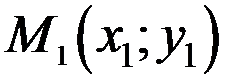 і
і  кінців цього відрізка за допомогою рівностей
кінців цього відрізка за допомогою рівностей ,
, 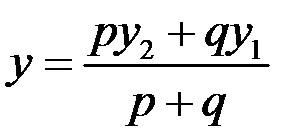 ,
,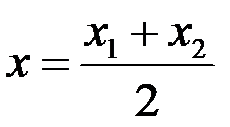 ,
, 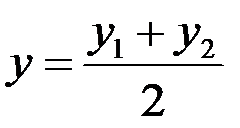 .
.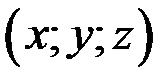 рівні напівсумі відповідних координат точок В і С, отже, х = -3, у = 5, z = 3.Медіану AN точка М ділить у відношенні
рівні напівсумі відповідних координат точок В і С, отже, х = -3, у = 5, z = 3.Медіану AN точка М ділить у відношенні 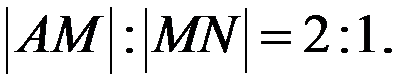 , тому координати
, тому координати 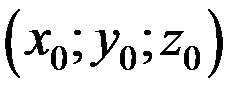 центру мас розглянутого трикутника рівні:
центру мас розглянутого трикутника рівні: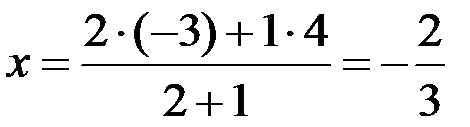 ,
, 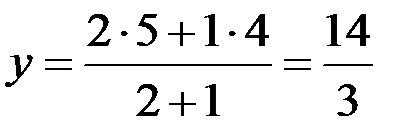 ,
, 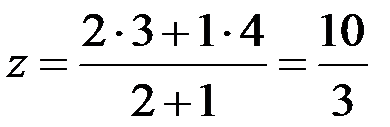 .
. .
.