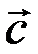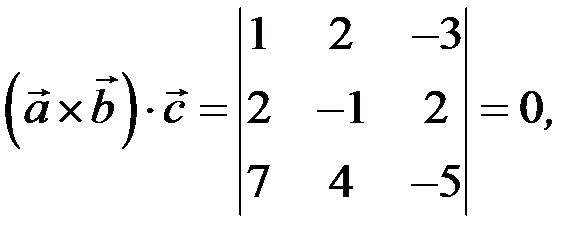1. Розглянемо три вектори 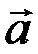 ,
, 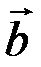 і
і 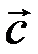 , які не лежать на одній площині.
, які не лежать на одній площині.
Побудуємо на цих векторах, як на ребрах, що виходить із однієї точки, паралелепіпед. Знайдемо об’єм паралелепіпеда: 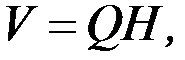
де Q – площа основи, а Н – висота. Згідно з означенням векторного добутку двох векторів, 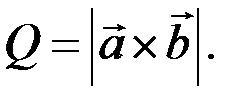
Висота паралелепіпеда Н дорівнює модулю проекції вектора 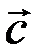 на вектор
на вектор 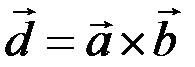 :
: 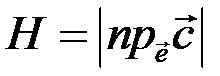 , де
, де  – одиничний вектор векторного добутку
– одиничний вектор векторного добутку 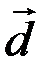 .
.
Таким чином,  Отже, геометрично змішаний добуток трьох векторів
Отже, геометрично змішаний добуток трьох векторів 
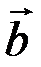 і
і 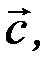 взятий за абсолютною величиною, є об’ємом паралелепіпеда, побудованого на векторах, які перемножуються, як на ребрах, що виходять з однієї точки.
взятий за абсолютною величиною, є об’ємом паралелепіпеда, побудованого на векторах, які перемножуються, як на ребрах, що виходять з однієї точки.
2. Змішаний добуток трьох векторів додатний, якщо розміщення векторів відповідає правій системі координат, і від’ємний, якщо розміщення векторів відповідає лівій системі координат.
Таким чином:
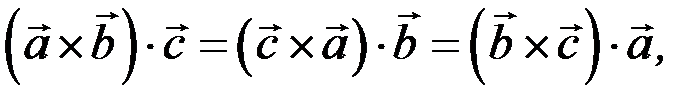

3. Три вектори 
 і
і 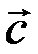 , відмінні від нуль-вектора, лежать на одній і тій самій площині, тобто є лінійно залежними, тоді і тільки тоді, коли їхній змішаний добуток дорівнює нулю.
, відмінні від нуль-вектора, лежать на одній і тій самій площині, тобто є лінійно залежними, тоді і тільки тоді, коли їхній змішаний добуток дорівнює нулю.
4. Нехай задано три вектори в координатній формі:
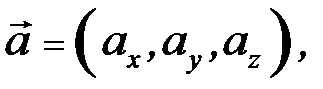
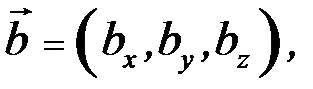
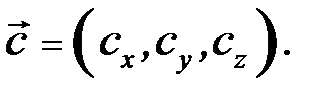
Тоді їхній змішаний добуток
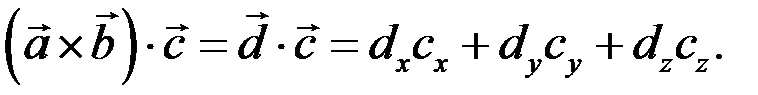
Як відомо,

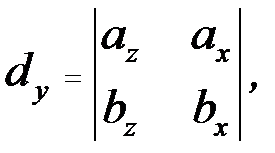

Отже,

Таким чином, змішаний добуток векторів, заданий в координатній формі, дорівнює
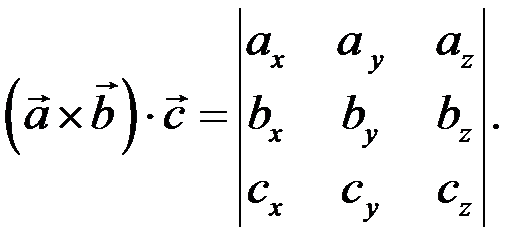
Можна записати у вигляді 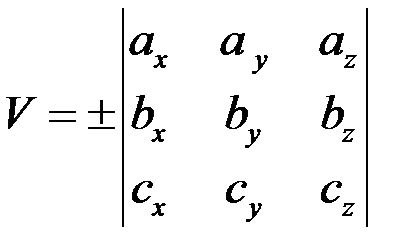 де знак «+» треба брати тоді, колі значення визначника додатне, і знак «–» тоді, коли це значення від’ємне. Якщо вектори
де знак «+» треба брати тоді, колі значення визначника додатне, і знак «–» тоді, коли це значення від’ємне. Якщо вектори 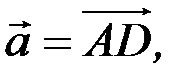
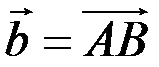 ,
, 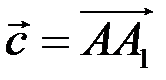 задано координатами їхніх початку і кінця, тобто точками
задано координатами їхніх початку і кінця, тобто точками 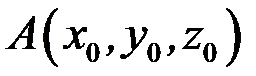 ,
, 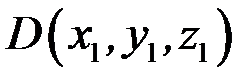 ,
, 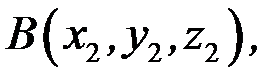
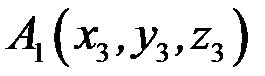 , то
, то 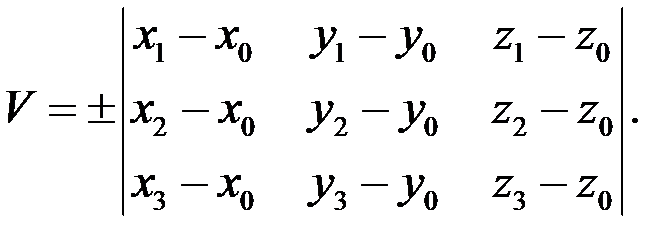
Умову компланарності трьох векторів можна записати у вигляді
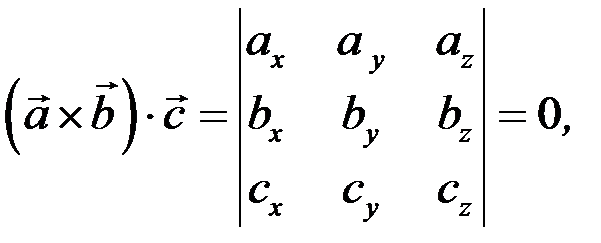
або 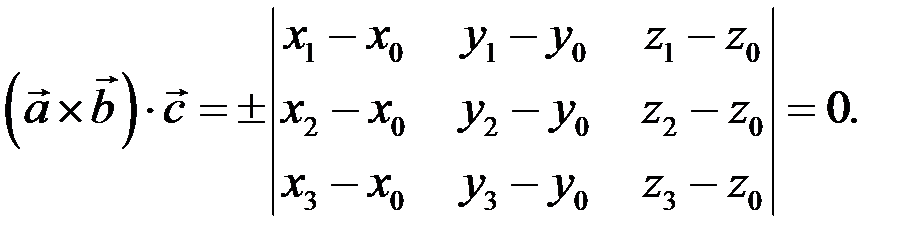
Аналогічно знаходимо умову приналежності чотирьох точок 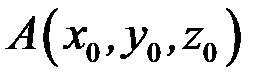 ,
, 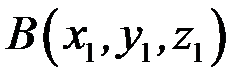 ,
, 
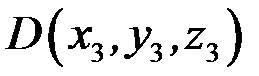 тривимірного простору однієї і тій самій площині (рис. 2.6). Дані точки лежать в одній площині, якщо вектори
тривимірного простору однієї і тій самій площині (рис. 2.6). Дані точки лежать в одній площині, якщо вектори 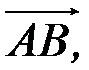
 ,
, 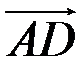 лежать у тій самій площині, а це буде тоді й тільки тоді, коли
лежать у тій самій площині, а це буде тоді й тільки тоді, коли 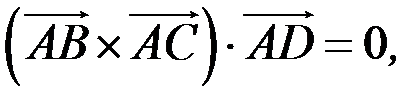 або
або
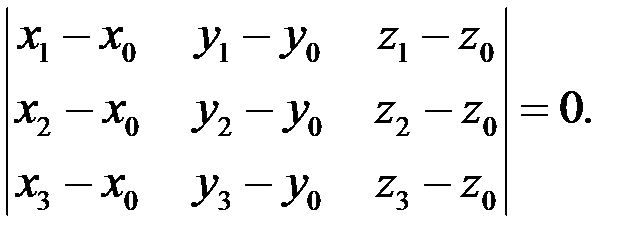
Розглянемо застосування змішаного добутку векторів до обчислення об’єму трикутної піраміди. Нехай вершини трикутної піраміди (рис. 3.6) лежить у точках 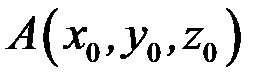 ,
, 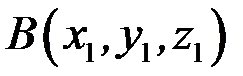 ,
, 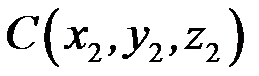 і
і 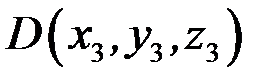 .
.
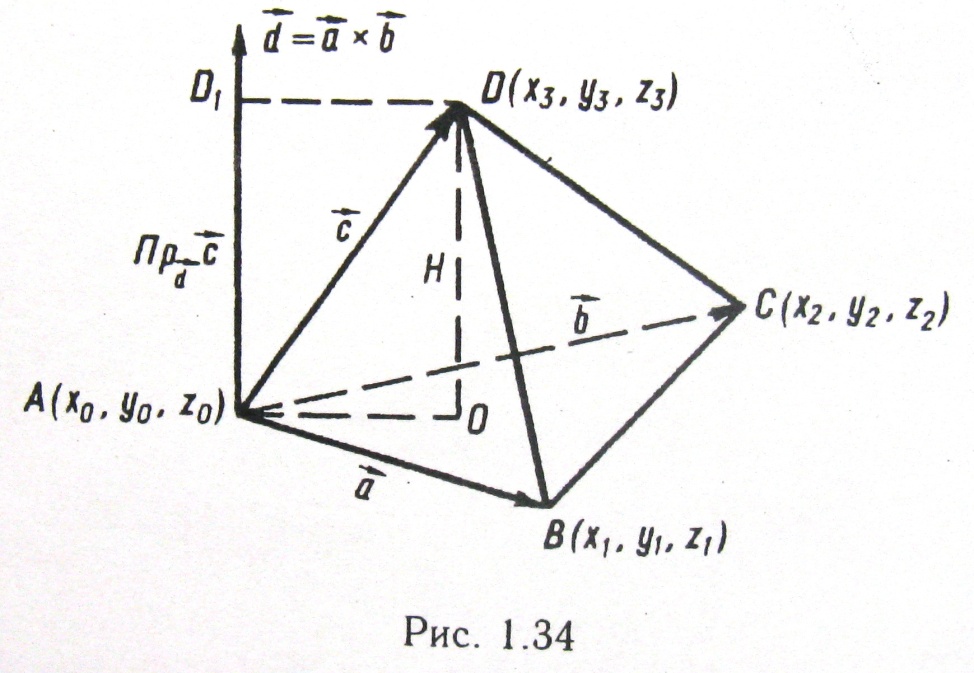
Рис. 5.6.
Площа трикутника 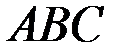 (основи піраміди) позначимо через Q, а її висоту |DO| – через Н. Об’єм піраміди
(основи піраміди) позначимо через Q, а її висоту |DO| – через Н. Об’єм піраміди 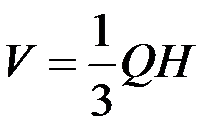 . Знайдемо вектори:
. Знайдемо вектори:
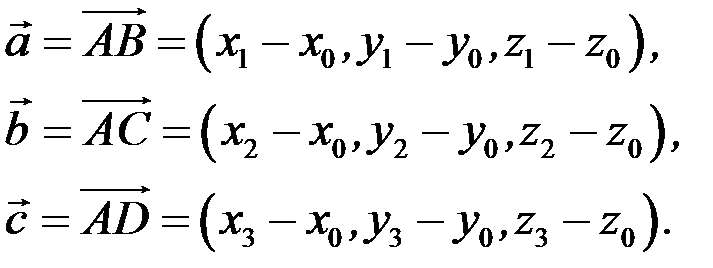
Тоді
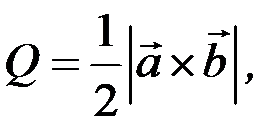 а
а 
Таким чином,
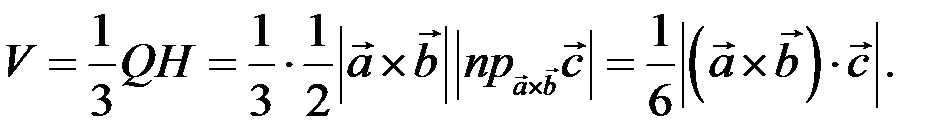
Тобто об’єм трикутної піраміди дорівнює 1/6 модуля змішаного добутку векторів, які збігаються з ребрами піраміди, що виходять з однієї і тієї самої вершини:
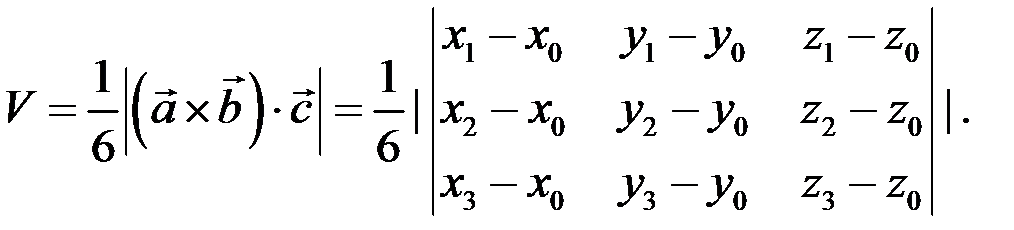
◄Приклад 5.8. Визначити, чи будуть лінійно залежними вектори
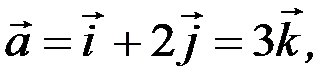
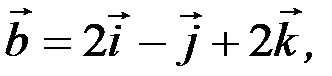
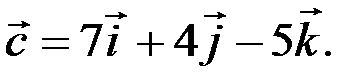
Розв’язання. Обчислимо змішаний добуток векторів 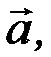
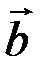 і
і 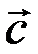
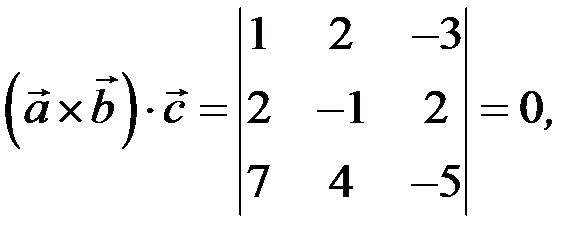
тобто дані вектори лінійно залежні.
Відповідь: лінійно залежні.


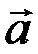 ,
, 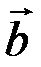 і
і 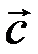 , які не лежать на одній площині.
, які не лежать на одній площині.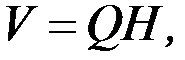
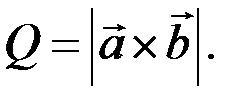
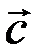 на вектор
на вектор 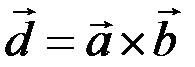 :
: 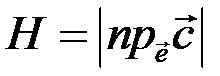 , де
, де  – одиничний вектор векторного добутку
– одиничний вектор векторного добутку 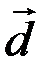 .
. Отже, геометрично змішаний добуток трьох векторів
Отже, геометрично змішаний добуток трьох векторів 
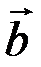 і
і 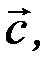 взятий за абсолютною величиною, є об’ємом паралелепіпеда, побудованого на векторах, які перемножуються, як на ребрах, що виходять з однієї точки.
взятий за абсолютною величиною, є об’ємом паралелепіпеда, побудованого на векторах, які перемножуються, як на ребрах, що виходять з однієї точки.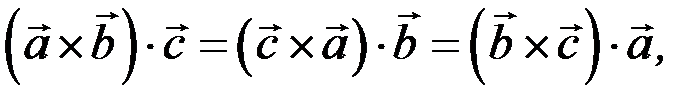

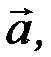
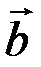 і
і 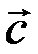 , відмінні від нуль-вектора, лежать на одній і тій самій площині, тобто є лінійно залежними, тоді і тільки тоді, коли їхній змішаний добуток дорівнює нулю.
, відмінні від нуль-вектора, лежать на одній і тій самій площині, тобто є лінійно залежними, тоді і тільки тоді, коли їхній змішаний добуток дорівнює нулю.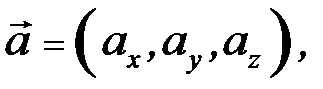
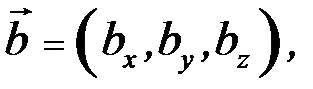
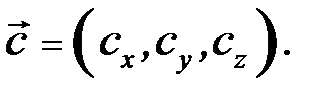
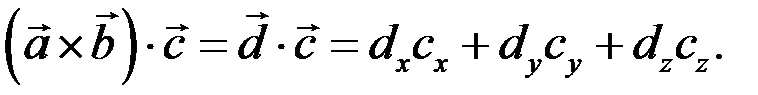

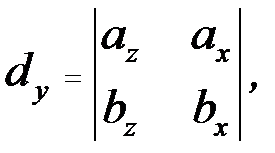


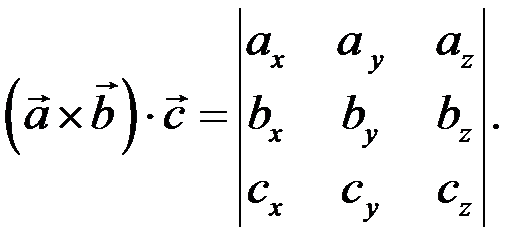
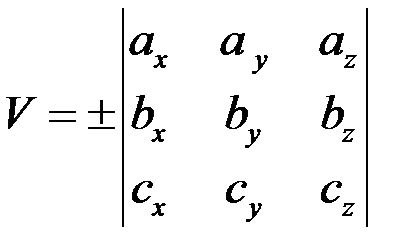 де знак «+» треба брати тоді, колі значення визначника додатне, і знак «–» тоді, коли це значення від’ємне. Якщо вектори
де знак «+» треба брати тоді, колі значення визначника додатне, і знак «–» тоді, коли це значення від’ємне. Якщо вектори 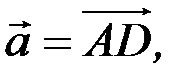
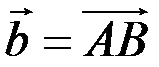 ,
, 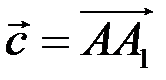 задано координатами їхніх початку і кінця, тобто точками
задано координатами їхніх початку і кінця, тобто точками 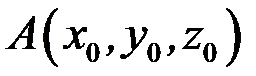 ,
, 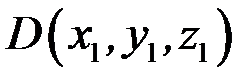 ,
, 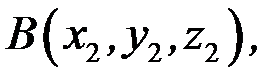
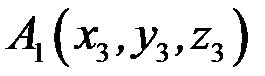 , то
, то 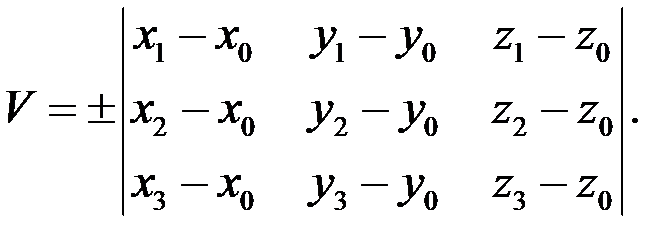
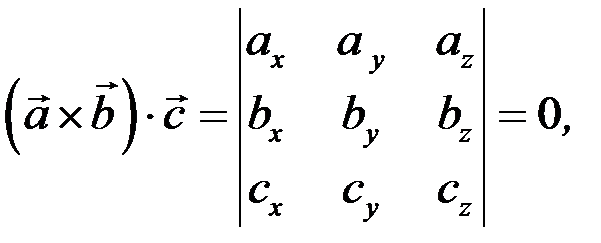
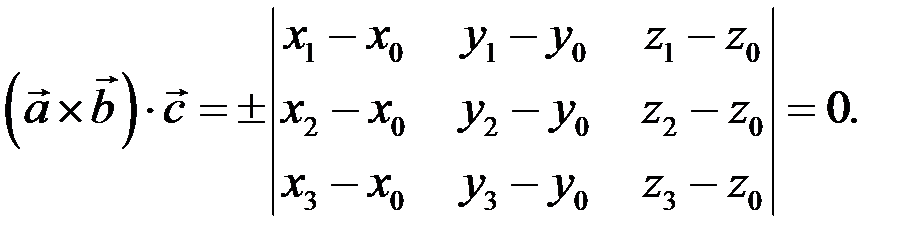
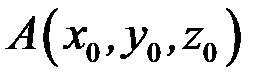 ,
, 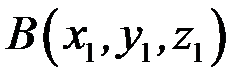 ,
, 
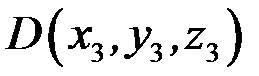 тривимірного простору однієї і тій самій площині (рис. 2.6). Дані точки лежать в одній площині, якщо вектори
тривимірного простору однієї і тій самій площині (рис. 2.6). Дані точки лежать в одній площині, якщо вектори 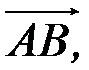
 ,
, 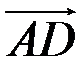 лежать у тій самій площині, а це буде тоді й тільки тоді, коли
лежать у тій самій площині, а це буде тоді й тільки тоді, коли 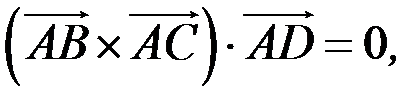 або
або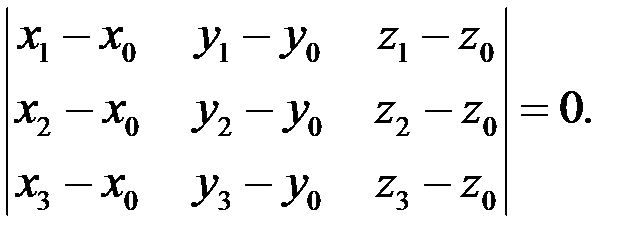
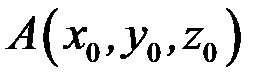 ,
, 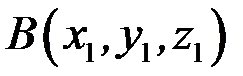 ,
, 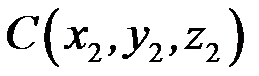 і
і 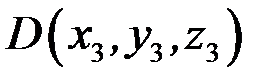 .
.
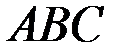 (основи піраміди) позначимо через Q, а її висоту |DO| – через Н. Об’єм піраміди
(основи піраміди) позначимо через Q, а її висоту |DO| – через Н. Об’єм піраміди 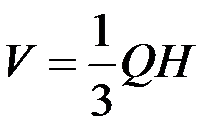 . Знайдемо вектори:
. Знайдемо вектори: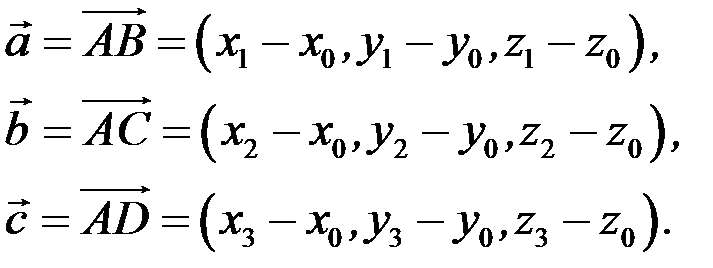
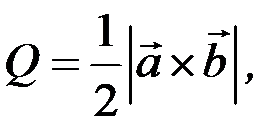 а
а 
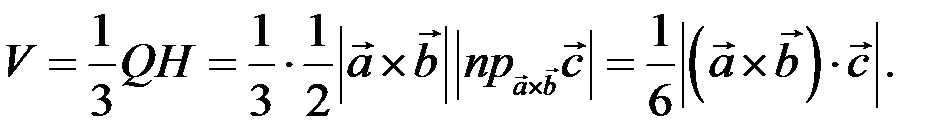
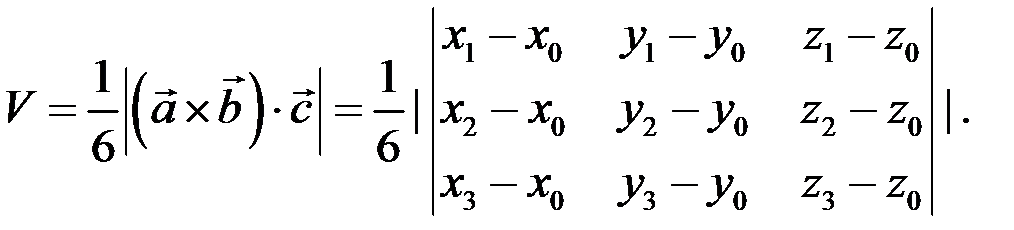
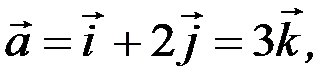
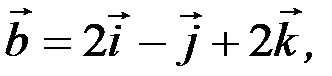
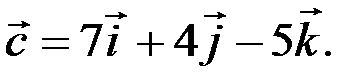
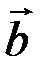 і
і