Визначення 2.9. Множина всіх елементів  , яким відповідає елемент
, яким відповідає елемент 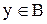 , називається прообразом елемента
, називається прообразом елемента 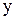 в множині
в множині 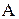 при відповідності
при відповідності 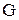 .
.
Приклад 2.6.Дано множини 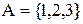 і
і 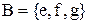 . Для відповідності
. Для відповідності 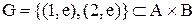 область визначення є проекція на першу вісь:
область визначення є проекція на першу вісь: 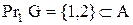 ; область значень – проекція на другу вісь:
; область значень – проекція на другу вісь: 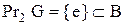 ;
; 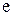 – образ елементів 1, 2 у множині
– образ елементів 1, 2 у множині 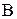 при відповідності
при відповідності 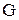 ; 1, 2 є прообразами елемента
; 1, 2 є прообразами елемента 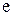 при відповідності
при відповідності 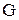 .
.
Відповідності прийнято ілюструвати за допомогою діаграм. Для приклада 2.6 діаграма наведена на рис. 2.1.
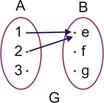
Рис. 2.1. Діаграма відповідності 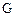 із приклада 2.6
із приклада 2.6
Визначення 2.10. Відповідність 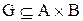 називається всюди визначеною, якщо її проекція на першу вісь співпадає з множиною відправлення:
називається всюди визначеною, якщо її проекція на першу вісь співпадає з множиною відправлення: 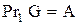 , тобто у відповідності задіяні всі елементи з області визначення
, тобто у відповідності задіяні всі елементи з області визначення 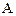 . У противному випадку відповідність є частковою.
. У противному випадку відповідність є частковою.
Приклад 2.6 ілюструє часткову відповідність, тому що 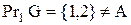 .
.
Приклад 2.7. Для відповідності 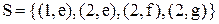
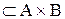 (рис. 2.2), де
(рис. 2.2), де 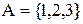 ,
, 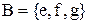 , проекція на першу вісь співпадає з множиною відправлення
, проекція на першу вісь співпадає з множиною відправлення  :
: 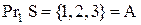 .
.
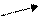
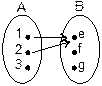
S
Рис. 2.2. Діаграма відповідності S із приклада 2.7
Визначення 2.11. Відповідність 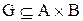 називається сур’єктивною, якщо її проекція на другу вісь співпадає з множиною прибуття:
називається сур’єктивною, якщо її проекція на другу вісь співпадає з множиною прибуття:  , тобто у відповідності задіяні всі елементи з області значень
, тобто у відповідності задіяні всі елементи з області значень 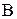 .
.
Приклад 2.8. Для відповідності 
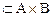 (рис. 2.3), де
(рис. 2.3), де 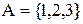 ,
, 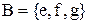 , проекція на другу вісь співпадає з множиною прибуття
, проекція на другу вісь співпадає з множиною прибуття 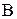 :
: 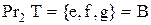 .
.

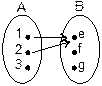
Т
Рис. 2.3. Діаграма відповідності Т із приклада 2.8
Визначення 2.12. Відповідність 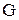 називається ін’єктивною (in), якщо різні елементи з його області визначення
називається ін’єктивною (in), якщо різні елементи з його області визначення 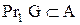 мають різні образи в його області значень
мають різні образи в його області значень 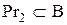 , тобто прообразом будь-якого елемента з області значень є єдиний елемент із області визначення (інакше – різні елементи з області визначення мають різні образи):
, тобто прообразом будь-якого елемента з області значень є єдиний елемент із області визначення (інакше – різні елементи з області визначення мають різні образи):
 . (2.6)
. (2.6)
Отже, при ін’єктивній відповідності кожний образ має єдиний прообраз. Це означає, що в діаграмі ін’єктивної відповідності немає збіжних стрілок.
Приклад 2.9. Відповідності 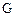 ,
, 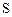 і
і 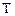 із прикладів 2.6–2.8 не є ін’єктивними, оскільки образ
із прикладів 2.6–2.8 не є ін’єктивними, оскільки образ 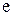 має два прообрази – елементи 1, 2 у множині
має два прообрази – елементи 1, 2 у множині 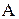 . До того ж у відповідності
. До того ж у відповідності 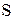 образ
образ 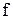 також має два прообрази – елементи 2 і 3.
також має два прообрази – елементи 2 і 3.
Приклад 2.10. Відповідність 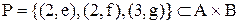 де
де 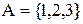 ,
, 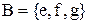 , є ін’єктивною, так як образи з множини
, є ін’єктивною, так як образи з множини 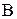 мають єдині прообрази в множині
мають єдині прообрази в множині 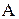 (рис. 2.4).
(рис. 2.4).
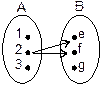
Р
Рис. 2.4. Діаграма відповідності Р із приклада 2.10
Визначення 2.13. Відповідність 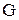 називається функціональною (однозначною), якщо образом будь-якого елемента з області визначення є єдиний елемент із області значень, тобто
називається функціональною (однозначною), якщо образом будь-якого елемента з області визначення є єдиний елемент із області значень, тобто 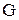 – функціонально, якщо
– функціонально, якщо
 . (2.7)
. (2.7)
Діаграма функціональної відповідності не має розбіжних стрілок.
Приклад 2.11. Відповідність 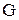 із приклада 2.6 є функціональною, тому що кожному прообразу відповідає єдиний образ: прообразу 1 відповідає образ
із приклада 2.6 є функціональною, тому що кожному прообразу відповідає єдиний образ: прообразу 1 відповідає образ 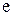 , прообразу 2 відповідає також один образ –
, прообразу 2 відповідає також один образ – 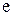 . Відповідність
. Відповідність 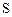 із приклада 2.7. не є функціональною, оскільки існує прообраз – елемент 2, у якого одночасно два образи – елементи
із приклада 2.7. не є функціональною, оскільки існує прообраз – елемент 2, у якого одночасно два образи – елементи 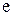 й
й 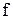 .
.
Визначення 2.14.Бієктивна (взаємо-однозначна) відповідність – це відповідність, що є всюди визначеною, сур’єктивною, ін’єктивною, функціональною, тобто має всі властивості одночасно.
Биекцію (бієктивну або взаємо-однозначну відповідність) можна встановити тільки між множинами однакових потужностей.
Приклад 2.12. Для відповідності 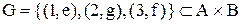 (рис. 2.5), де
(рис. 2.5), де 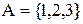 ,
, 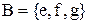 , характерні всі властивості, отже, вона є бієктивною.
, характерні всі властивості, отже, вона є бієктивною.
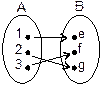
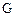
Рис. 2.5. Діаграма відповідності 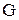 із приклада 2.12
із приклада 2.12
Приклад 2.13.Розглядається відповідність 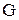 , що геометрично представлена на рис. 2.6. Вона переводить відрізок
, що геометрично представлена на рис. 2.6. Вона переводить відрізок 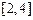 дійсної осі
дійсної осі 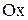 у відрізок
у відрізок 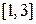 дійсної осі
дійсної осі 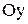 :
: 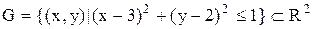 . Відповідність
. Відповідність 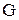 не є функціональною, тому що образом числа 3, що лежить на осі абсцис, є відрізок
не є функціональною, тому що образом числа 3, що лежить на осі абсцис, є відрізок 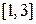 осі ординат, а не єдиний елемент:
осі ординат, а не єдиний елемент:  . Дуга
. Дуга 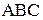 є прикладом функціональної відповідності.
є прикладом функціональної відповідності.
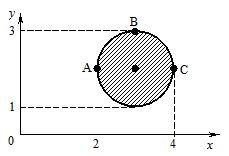
Рис. 2.6. Ілюстрація відповідності до прикладу 2.13
2.4. Функції. Відображення
Визначення 2.15. Функцією називається функціональна відповідність
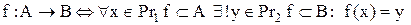 , (2.8)
, (2.8)
де х – аргумент; у – значення функції на елементі х.
Визначення 2.16. Відображенням множини 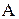 в множину
в множину 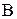 називається всюди визначена функція;
називається всюди визначена функція; 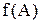 – образ множини
– образ множини 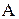 при відображенні
при відображенні 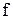 .
.
Приклад 2.14.Відповідність 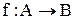 (рис. 2.7) є функціональною (функцією), оскільки кожному прообразу відповідає єдиний образ; всюди визначеною, тому що
(рис. 2.7) є функціональною (функцією), оскільки кожному прообразу відповідає єдиний образ; всюди визначеною, тому що 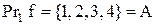 ; отже, f – відображення; не є сур’єктивною:
; отже, f – відображення; не є сур’єктивною: 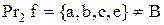 (елемент d не має прообразу в множині
(елемент d не має прообразу в множині 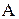 ).
).
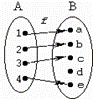
Рис. 2.7. Приклад функції і відображення
Визначення 2.17. Якщо для відповідності  існує відповідність
існує відповідність 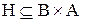 така, що
така, що 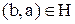 тоді й тільки тоді, коли
тоді й тільки тоді, коли 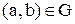 , тоді відповідність
, тоді відповідність 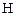 називається зворотною до
називається зворотною до 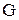 і позначається
і позначається  , тобто
, тобто
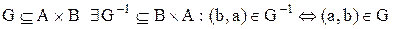 .
.
Визначення 2.18. Зворотною функцією 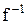 називається відповідність, зворотна до функції
називається відповідність, зворотна до функції 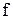 , тобто якщо зворотна до
, тобто якщо зворотна до 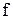 відповідність є функціональною, то вона називається зворотною функцією й позначається
відповідність є функціональною, то вона називається зворотною функцією й позначається 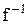 .
.
Приклад 2.15. Різні види кодування (кодування букв абеткою Морзе, подання чисел у різних системах числення, секретні шифри, вхідні та вихідні номери в діловій переписці) є відповідностями між кодованими об’єктами й кодами, що привласнюються їм. Ці відповідності, як правило, мають всі властивості взаємо-однозначної відповідності, крім сур’єктивності. Єдиність образу й прообразу в кодуванні гарантує однозначність шифрування й дешифрування. Відсутність сур’єктивності означає, що не кожний код має сенс. Наприклад, кодування телефонів сьомизначними номерами не є сур’єктивним, оскільки деякі номери не відповідають ніяким телефонам. Для кодувальної функції, що кожному об'єкту зі своєї області значень ставить у відповідність деякий код, зворотною буде декодувальна функція, що кожному коду ставить у відповідність закодований цим кодом об’єкт. Якщо кодувальна функція, не є сур’єктивною, то декодувальна функція не всюди визначена.
Визначення 2.19. Нехай дані функції 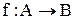 й
й  . Функція
. Функція  називається композицією функцій
називається композицією функцій 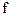 і
і 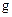 (позначення
(позначення  ), якщо має місце рівність
), якщо має місце рівність 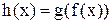 , де
, де  . Композиція є послідовне застосування функцій
. Композиція є послідовне застосування функцій 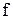 і
і 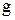 , при цьому
, при цьому 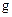 застосовується до результату функції
застосовується до результату функції 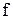 .
.
Приклад 2.16. Розглядається триелементна множина 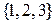 і два перетворення
і два перетворення  й
й 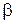 цієї множини:
цієї множини:  і
і  , де запис
, де запис 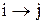 означає, що елементу
означає, що елементу  ставиться у відповідність елемент
ставиться у відповідність елемент 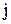 , тобто
, тобто  переходить у
переходить у 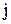 . Для завдання перетворення кінцевих множин використовується запис:
. Для завдання перетворення кінцевих множин використовується запис: 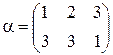 ,
, 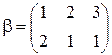 . Композиція перетворень – є нове перетворення:
. Композиція перетворень – є нове перетворення: 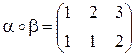 ,
, 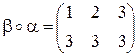 .
.
Приклад 2.17. При діагностуванні мікросхем напівпровідникової пам’яті роботу дешифратора адреса можна представити у вигляді графа адресної дешифрації, що показує відповідність між адресами й елементами пам’яті. При правильній роботі спостерігається взаємо-однозначна відповідність між призначеною адресою ліворуч і місцем елемента праворуч (рис. 2.8, а). При несправності дешифратора спостерігається порушення взаємо-однозначної відповідності в графі адресної дешифрації (рис. 2.8, б).

а б
Рис. 2.8. Граф адресної дешифрації: а – випадок справної схеми;
б – випадок з несправністю
2.5. Контрольні питання
1. Чи можуть повторюватися елементи вектора?
2. Як визначається довжина вектора?
3. Як визначається декартів добуток двох множин?
4. Як визначається декартів добуток 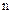 множин?
множин?
5. Що є елементами декартова добутку двох множин?
6. Що є об'єктами декартова добутку 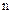 множин?
множин?
7. Як визначається вектор?
8. Як визначається довжина (розмірність) вектора?
9. Чому дорівнює потужність декартова добутку 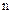 множин?
множин?
10. Чи є декартів добуток множин комутативним?
11. Що являє собою декартовий ступінь?
12. Чи вірно:  ?
?
13. Що таке відповідність?
14. Що називається проекцією вектора на 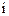 -у вісь?
-у вісь?
3. Відношення. Алгебра відношень
3.1 Поняття відношення
Фундаментальним у дискретній математиці є поняття відношення, що використовують для позначення зв’язку між об’єктами або іншими поняттями.
Визначення 3.1.Підмножина 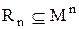 називається
називається 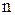 -місцевим відношенням на множині
-місцевим відношенням на множині  , де індекс
, де індекс 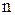 визначає ступінь відношення (
визначає ступінь відношення (  ).
).
Елементи 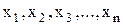 перебувають у відношенні
перебувають у відношенні 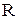 , якщо
, якщо 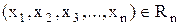 . При цьому:
. При цьому: 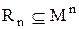 – n-арне відношення;
– n-арне відношення; 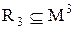 – тернарне відношення;
– тернарне відношення;  – бінарне відношення.
– бінарне відношення. 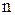 -місцеве відношення утворене векторами однакової довжини, тобто
-місцеве відношення утворене векторами однакової довжини, тобто 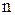 -мірними векторами.
-мірними векторами.
Часто індекс 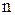 у позначенні відношення опускається. Як правило, відношення позначаються прописними буквами латинського алфавіту або малими літерами грецького алфавіту.
у позначенні відношення опускається. Як правило, відношення позначаються прописними буквами латинського алфавіту або малими літерами грецького алфавіту.
3.2 Операції над відношеннями
Відношення у сукупності з операціями утворюють реляційну алгебру (алгебру відношень) 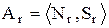 , що використовується для побудови реляційних баз даних, а також для компіляторів, операційних систем. Носій реляційної алгебри
, що використовується для побудови реляційних баз даних, а також для компіляторів, операційних систем. Носій реляційної алгебри  – множина відношень; сигнатура
– множина відношень; сигнатура 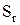 – набір операцій над відношеннями: об'єднання
– набір операцій над відношеннями: об'єднання 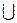 , перетинання
, перетинання 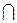 , різниця
, різниця 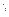 , розширений декартів добуток
, розширений декартів добуток 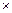 .
.
Визначення 3.2. Відношення  і
і 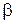 називаються сумісними, якщо вони мають однаковий ступінь, який визначається -арністью відношень:
називаються сумісними, якщо вони мають однаковий ступінь, який визначається -арністью відношень: 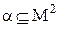 – бінарне відношення (ступінь 2);
– бінарне відношення (ступінь 2); 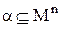 – n-арне відношення (ступінь n).
– n-арне відношення (ступінь n).
Для сумісних відношень мають місце ті ж операції, що й для множин. Розглянемо 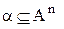 ,
,  (або
(або  ).
).
Визначення 3.3. Об'єднання відношень 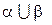 – множина всіх векторів (кортежів), кожний з яких належить
– множина всіх векторів (кортежів), кожний з яких належить  або
або 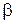 :
:
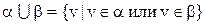 . (3.1)
. (3.1)
Визначення 3.4. Перетинання відношень  – множина всіх векторів, кожний з яких належить одночасно як
– множина всіх векторів, кожний з яких належить одночасно як  , так і
, так і 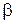 :
:
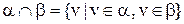 . (3.2)
. (3.2)
Визначення 3.5. Різниця відношень  – множина всіх векторів, що належать
– множина всіх векторів, що належать  і не належать
і не належать 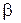 :
:
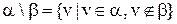 . (3.3)
. (3.3)
Визначення 3.6. Доповнення бінарного відношення 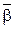 до універсального відношення
до універсального відношення 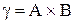 є різниця
є різниця  :
:
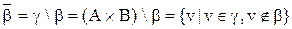 . (3.4)
. (3.4)
Формулу (3.5) можна поширити на 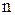 -місцеве відношення
-місцеве відношення 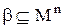 :
:
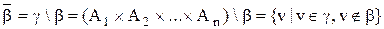 . (3.5)
. (3.5)
Визначення 3.7. Розширений декартів добуток відношень 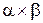 (
(  і
і 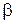 можуть бути несумісними) – множина всіх векторів
можуть бути несумісними) – множина всіх векторів  таких, що
таких, що  – конкатенація кортежу
– конкатенація кортежу 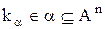 з кортежем
з кортежем 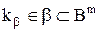 (конкатенація кожного вектора з кожним):
(конкатенація кожного вектора з кожним):
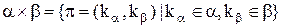 . (3.6)
. (3.6)
Потужність розширеного декартова добутку визначає кількість векторів у ньому й обчислюється як добуток потужностей співмножників:
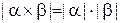 . (3.7)
. (3.7)
Ступінь розширеного декартова добутку визначається сумою ступенів відношень-множників (та визначає довжину векторів):
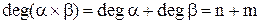 . (3.8)
. (3.8)
Приклад 3.1. Дані сумісні тернарні відношення 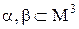 :
:
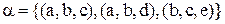 ,
, 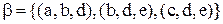 .
.
Потрібно визначити об'єднання, перетинання, різницю відношень  і
і 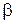 . Згідно (3.1)-(3.3) об'єднання дає:
. Згідно (3.1)-(3.3) об'єднання дає:
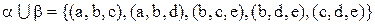 ;
;
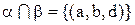 ;
;
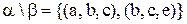 .
.
Приклад 3.2. Дані множини  ,
, 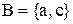 , їх декартови квадрати дорівнюють:
, їх декартови квадрати дорівнюють:
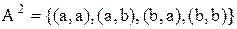 ;
; 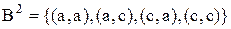 .
.
Нехай бінарні відносини  й
й 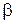 задані таким способом:
задані таким способом:
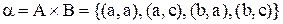 – універсальне відношення,
– універсальне відношення,
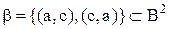 .
.
Тоді доповнення відношення 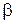 до універсального відношення
до універсального відношення  визначається за формулою (3.4):
визначається за формулою (3.4):
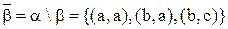 .
.
Приклад 3.3. Бінарне відношення  й тернарне відношення
й тернарне відношення 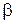 задані так:
задані так:
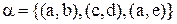 ,
, 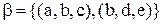 .
.
Тоді розширений декартів добуток 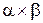 визначається згідно з (3.6) як конкатенація наступним чином:
визначається згідно з (3.6) як конкатенація наступним чином:
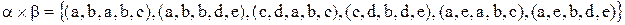 .
.
3.3 Алгебра відношень
Алгебра відношень і модель (множина із заданим відношенням) знаходять широке застосування при формалізації реальних об'єктів, при створенні інформаційного забезпечення – розробці інформаційної бази даних. Основою побудови реляційної бази даних є двовимірна таблиця, кожний стовпчик якої відповідає домену (або атрибуту, що відповідає частині домену), рядок – кортежу значень атрибутів, що перебувають у відношенні 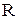 .
.
Приклад 3.4. Таблиця визначає відношення реляційної моделі даних
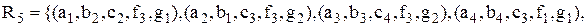
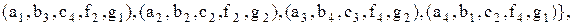
або
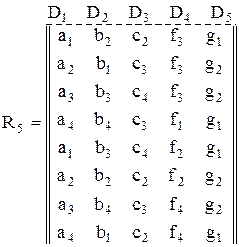 , (3.9)
, (3.9)
де відношення п'ятого ступеня 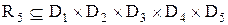 , у якому співмножник – стовпець
, у якому співмножник – стовпець 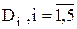 – є доменом. Його елементами служать значення атрибутів. Порядок стовпців у таблиці фіксований, рядки в загальному випадку можуть розташовуватися довільно (рядки таблиці – кортежі, стовпці – осі або домени).
– є доменом. Його елементами служать значення атрибутів. Порядок стовпців у таблиці фіксований, рядки в загальному випадку можуть розташовуватися довільно (рядки таблиці – кортежі, стовпці – осі або домени).


 , яким відповідає елемент
, яким відповідає елемент 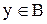 , називається прообразом елемента
, називається прообразом елемента 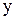 в множині
в множині 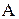 при відповідності
при відповідності 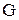 .
.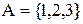 і
і 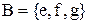 . Для відповідності
. Для відповідності 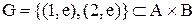 область визначення є проекція на першу вісь:
область визначення є проекція на першу вісь: 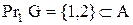 ; область значень – проекція на другу вісь:
; область значень – проекція на другу вісь: 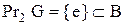 ;
; 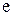 – образ елементів 1, 2 у множині
– образ елементів 1, 2 у множині 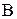 при відповідності
при відповідності 
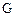 із приклада 2.6
із приклада 2.6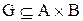 називається всюди визначеною, якщо її проекція на першу вісь співпадає з множиною відправлення:
називається всюди визначеною, якщо її проекція на першу вісь співпадає з множиною відправлення: 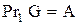 , тобто у відповідності задіяні всі елементи з області визначення
, тобто у відповідності задіяні всі елементи з області визначення 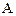 . У противному випадку відповідність є частковою.
. У противному випадку відповідність є частковою.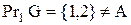 .
.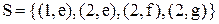
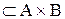 (рис. 2.2), де
(рис. 2.2), де 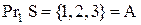 .
.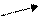
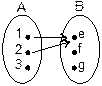
 , тобто у відповідності задіяні всі елементи з області значень
, тобто у відповідності задіяні всі елементи з області значень 
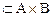 (рис. 2.3), де
(рис. 2.3), де 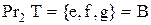 .
.
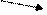
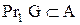 мають різні образи в його області значень
мають різні образи в його області значень 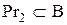 , тобто прообразом будь-якого елемента з області значень є єдиний елемент із області визначення (інакше – різні елементи з області визначення мають різні образи):
, тобто прообразом будь-якого елемента з області значень є єдиний елемент із області визначення (інакше – різні елементи з області визначення мають різні образи): . (2.6)
. (2.6)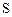 і
і 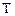 із прикладів 2.6–2.8 не є ін’єктивними, оскільки образ
із прикладів 2.6–2.8 не є ін’єктивними, оскільки образ 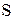 образ
образ 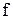 також має два прообрази – елементи 2 і 3.
також має два прообрази – елементи 2 і 3.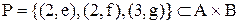 де
де 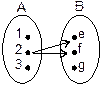
 . (2.7)
. (2.7)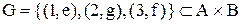 (рис. 2.5), де
(рис. 2.5), де 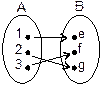
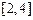 дійсної осі
дійсної осі 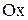 у відрізок
у відрізок 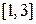 дійсної осі
дійсної осі 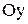 :
: 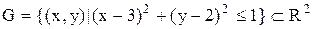 . Відповідність
. Відповідність  . Дуга
. Дуга 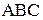 є прикладом функціональної відповідності.
є прикладом функціональної відповідності.
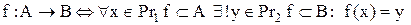 , (2.8)
, (2.8)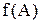 – образ множини
– образ множини 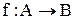 (рис. 2.7) є функціональною (функцією), оскільки кожному прообразу відповідає єдиний образ; всюди визначеною, тому що
(рис. 2.7) є функціональною (функцією), оскільки кожному прообразу відповідає єдиний образ; всюди визначеною, тому що 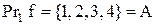 ; отже, f – відображення; не є сур’єктивною:
; отже, f – відображення; не є сур’єктивною: 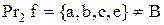 (елемент d не має прообразу в множині
(елемент d не має прообразу в множині 
 існує відповідність
існує відповідність 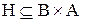 така, що
така, що 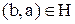 тоді й тільки тоді, коли
тоді й тільки тоді, коли 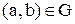 , тоді відповідність
, тоді відповідність 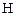 називається зворотною до
називається зворотною до  , тобто
, тобто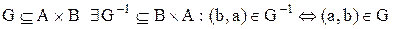 .
.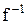 називається відповідність, зворотна до функції
називається відповідність, зворотна до функції 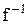 .
. . Функція
. Функція  називається композицією функцій
називається композицією функцій 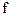 і
і 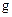 (позначення
(позначення  ), якщо має місце рівність
), якщо має місце рівність 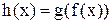 , де
, де 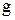 , при цьому
, при цьому 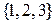 і два перетворення
і два перетворення  й
й 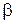 цієї множини:
цієї множини:  і
і  , де запис
, де запис 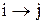 означає, що елементу
означає, що елементу  ставиться у відповідність елемент
ставиться у відповідність елемент 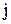 , тобто
, тобто 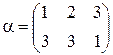 ,
, 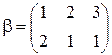 . Композиція перетворень – є нове перетворення:
. Композиція перетворень – є нове перетворення: 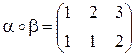 ,
, 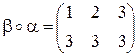 .
.
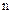 множин?
множин? ?
?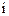 -у вісь?
-у вісь?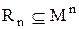 називається
називається 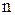 -місцевим відношенням на множині
-місцевим відношенням на множині  , де індекс
, де індекс  ).
).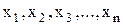 перебувають у відношенні
перебувають у відношенні 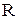 , якщо
, якщо 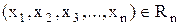 . При цьому:
. При цьому: 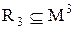 – тернарне відношення;
– тернарне відношення;  – бінарне відношення.
– бінарне відношення. 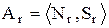 , що використовується для побудови реляційних баз даних, а також для компіляторів, операційних систем. Носій реляційної алгебри
, що використовується для побудови реляційних баз даних, а також для компіляторів, операційних систем. Носій реляційної алгебри  – множина відношень; сигнатура
– множина відношень; сигнатура 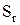 – набір операцій над відношеннями: об'єднання
– набір операцій над відношеннями: об'єднання 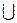 , перетинання
, перетинання 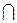 , різниця
, різниця 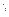 , розширений декартів добуток
, розширений декартів добуток 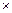 .
.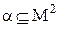 – бінарне відношення (ступінь 2);
– бінарне відношення (ступінь 2); 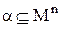 – n-арне відношення (ступінь n).
– n-арне відношення (ступінь n).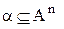 ,
,  (або
(або  ).
).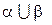 – множина всіх векторів (кортежів), кожний з яких належить
– множина всіх векторів (кортежів), кожний з яких належить 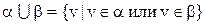 . (3.1)
. (3.1) – множина всіх векторів, кожний з яких належить одночасно як
– множина всіх векторів, кожний з яких належить одночасно як 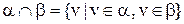 . (3.2)
. (3.2) – множина всіх векторів, що належать
– множина всіх векторів, що належать 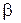 :
: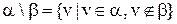 . (3.3)
. (3.3)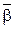 до універсального відношення
до універсального відношення 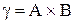 є різниця
є різниця  :
: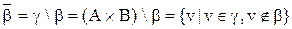 . (3.4)
. (3.4)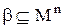 :
: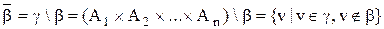 . (3.5)
. (3.5)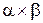 (
(  таких, що
таких, що 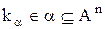 з кортежем
з кортежем 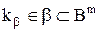 (конкатенація кожного вектора з кожним):
(конкатенація кожного вектора з кожним):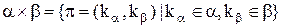 . (3.6)
. (3.6)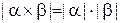 . (3.7)
. (3.7)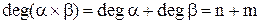 . (3.8)
. (3.8)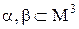 :
: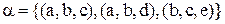 ,
, 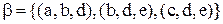 .
.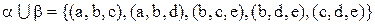 ;
;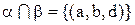 ;
;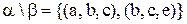 .
. ,
, 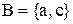 , їх декартови квадрати дорівнюють:
, їх декартови квадрати дорівнюють: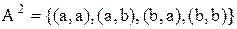 ;
; 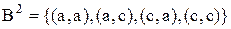 .
.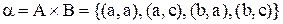 – універсальне відношення,
– універсальне відношення,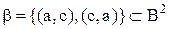 .
.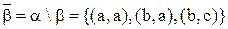 .
.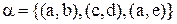 ,
, 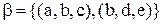 .
.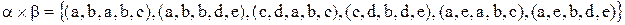 .
.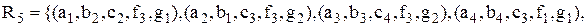
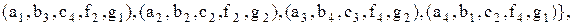
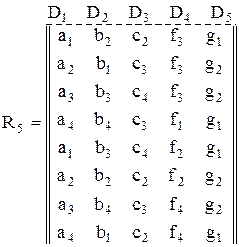 , (3.9)
, (3.9)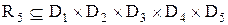 , у якому співмножник – стовпець
, у якому співмножник – стовпець 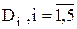 – є доменом. Його елементами служать значення атрибутів. Порядок стовпців у таблиці фіксований, рядки в загальному випадку можуть розташовуватися довільно (рядки таблиці – кортежі, стовпці – осі або домени).
– є доменом. Його елементами служать значення атрибутів. Порядок стовпців у таблиці фіксований, рядки в загальному випадку можуть розташовуватися довільно (рядки таблиці – кортежі, стовпці – осі або домени).