Пусть а=п(А) и мн.А разбито на попарно непересекающиеся равномощные подмножества. Если в- число элементов каждого подмн.в разбиении мн.А, то частным чисел а и в называется число подмножеств в этом разбиении. Если в- число подмн.в разбиении мн.А, то частным чисел а и в называется число элементов каждого подм. Действие нахождения частного называется делением, числа а и в называют соответственно делимым и делителем (проверяется правильность выполнения деления умножением). Частным нат.чисел а и в называется нат.число с, произведение которого и числа в равно а, т.е.а:в=с<=>а=с*в. П: 189:3=63, т.к.63*3=189. Теорема 1: для того чтобы частное двух нат.чисел а и в существовало, необходимо, чтобы в≤а. Док-во: пусть частное нат.чисел а и в существует. Это значит, что существует такое нат.число с, что а=с*в. Для нат.числа с верно утверждение 1≤с. Умножим обе части этого неравенства на в, получим в≤с*в или в≤а. Теорема 2: если частное нат.чисел а и в существует, то оно единственно. Док-во (методом от противного): предположим, что существуют два различных значения частного: а:в=с1 и а:в=с2, причём с1≠с2. Тогда по определению частного имеем: а=с1*в и а=с2*в. Отсюда с1*в=с2*в, тогда по св-ву сократимости умножения получим с1=с2. Последнее равенство противоречит предположению о том, что с1≠с2. Противоречие доказывает теорему. Частные случаи: 1.Пусть а≠0, в=0. Деление числа а на ) невозможно,т.к.не существует такого числа с, что 0*с=а≠0. 2.Пусть а=0 и в=0. Частное вида 0:0 не определено,т.к.0:0=с1 и 0:0=с2. Проверка показывает, что в каждом случае деление выполнено верно, поскольку с1*0=0 и с2*0=0. Правила деления: правило деления суммы на число- чтобы разделить сумму а и в на число с, достаточно разделить каждое слагаемое на это число с и полученные частные сложить,т.е. (а+в):с= а:с+в:с, если а⋮с и в⋮с. Док-во: так как а⋮с и в⋮с, то существуют такие нат.числа м и п, что м=а:с и п=в:с. По определению частного а=с*м и в=с*п. Тогда а+в=с*м+с*п= с*(м+п). Отсюда следует, что а+в делится на с и частное (а+в):с=м+п=а:с+в:с; правило деления числа на произведение: чтобы разделить число а на произведение чисел в и с, достаточно разделить число а на в(на с) и полученное частное разделить на с (на в),т.е. а:(в*с)= (а:в):с= (а:с):в. Док-во: пусть (а:в):с=х. По определению частного имеем а:в=с*х. Применив ещё раз определение частного, получим: а=в*(с*х)= (в*с)*х. Отсюда х=а:(вс). Таким образом, а:(вс)= (а:в):с; правило умножения числа на частное: чтобы умножить число на частное двух чисел, достаточно умножить это число на делимое и полученное произведение разделить на частное, т.е. а*(в:с)= (а*в):с.
Признаки делимости на 2,3,4,5,9,11.
Признаки делимости позволяют установить по записи чис¬ла делится ли оно на другое, не выполняя деления. Признак делимости на 2. Для того чтобы число х делилось на 2, необходимо и достаточно, чтобы его десятичная запись оканчивалась одной из цифр 0, 2, 4, 6, 8. П: 301924 делится на 2, т.к.заканчивается цифрой 4. Признак делимости на 3.Для того чтобы число х делилось на 3, необходимо и достаточно, чтобы сумма цифр его десятичной записи делилось на 3. П: 30192 делится на 3, т.к.сумма цифр этого числа 3+1+9+2=15 делится на 3. Признак делимости на 4. Для того чтобы число х делилось на 4, необходимо и достаточно, чтобы на 4 делилось двузначное число, образованное последними двумя цифрами десятичной записи числа х. П: 301924 делится на 4, т.к.последние две цифры образуют двузначное число 24, которое делится на 4. Признак делимости на 5. Для того чтобы число х делилось на 5, необходимо и достаточно, чтобы его десятичная запись оканчивалась цифрой 0 или 5. П: 301925 делится на 5, т.к.заканчивается цифрой 5. Признак делимости на 9. Для того чтобы число х делилось на 9, необходимо и достаточно, чтобы сум¬ма цифр его десятичной записи делилось на 9. П: 19242 делится на 9, т.к.сумма его цифр 1+9+2+4+2=18 делится на 9. Признак делимости на 11.Число делится на 11, тогда и только тогда, когда разность между суммой цифр на чётных местах и суммой цифр на нечетных местах делится на 11. П: 301928 делится на 11, т.к.разность между суммами цифр, стоящих на нечётных местах, и цифр, стоящих на чётных местах, составляет: (8+9+0)- (3+1+2)= 17-6=11, что делится на 11.
Простые и составные числа. Свойства простых чисел.
Натуральное число а, большее единицы, называется простым, если оно имеет только два различных делителя: единицу и само число а. Нат.число называется составным, если оно имеет более двух различных делителей. Число 7- простое, т.к.делится на 1 и на 7; 4- составное, т.к.делится на 1,2 и 4. 1- ни простое, ни составное число, т.к.имеет только один делитель. Число 0 также имеет более двух делителей, но его не считают составным числом, т.к.кол-во делителей у него бесконечное. Cв-ва простых чисел: Теорема 1: всякое нат.число, больше 1, имеет простой делитель. Док-во (методом от противного): пусть d- наименьший, не равный единице нат.делитель числа а. Требуется доказать, что d- простое число. Предположим, что d- составное число. Тогда d  t, следовательно, t
t, следовательно, t  d. Надо доказать, что t=1. По св-ву транзитивности отношения делимости имеем: а
d. Надо доказать, что t=1. По св-ву транзитивности отношения делимости имеем: а  d и d
d и d  t
t 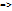 a
a  t. Т.к.число t натуральное, то t
t. Т.к.число t натуральное, то t 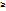 1. Если t
1. Если t  1, то t
1, то t  d противоречит тому, что d- наименьший делитель числа а. Если t=1, то это значит, что d- простое число. Теорема 2: наименьший простой делитель составного числа а не превосходит
d противоречит тому, что d- наименьший делитель числа а. Если t=1, то это значит, что d- простое число. Теорема 2: наименьший простой делитель составного числа а не превосходит  . Док-во: пусть а- составное число, а р- его наименьший простой делитель, тогда а=рв. При этом р
. Док-во: пусть а- составное число, а р- его наименьший простой делитель, тогда а=рв. При этом р 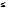 в. Умножим обе части неравенства на р. Получим р2
в. Умножим обе части неравенства на р. Получим р2 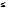 рв или р2
рв или р2 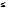 а, это значит, р
а, это значит, р  . Из этой теоремы следует, что если число а не делится ни на одно простое число, не превосходящее
. Из этой теоремы следует, что если число а не делится ни на одно простое число, не превосходящее  , то у него нет простых множителей, меньших этого числа, а значит, число а простое. П: покажем, что число 127 простое. Найдём корень квадратный из данного числа: 11
, то у него нет простых множителей, меньших этого числа, а значит, число а простое. П: покажем, что число 127 простое. Найдём корень квадратный из данного числа: 11 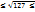 12. Мн.простых чисел, меньших 12, состоит из чисел 2,3,5,7,11. Т.к. 127 не делится ни на одно из этих простых чисел, то 127 само яв-ся простым числом.
12. Мн.простых чисел, меньших 12, состоит из чисел 2,3,5,7,11. Т.к. 127 не делится ни на одно из этих простых чисел, то 127 само яв-ся простым числом.
Теорема о бесконечности мн.простых чисел. Решето Эратосфена. Теорема Евклида
мн.простых чисел бесконечное. Док-во: предположим, что мн.простых чисел конечное, пусть это будут числа р1, р2, р3, …, рп. Образуем произведение этих простых чисел и прибавим к нему единицу. Получим число а=р1  р2
р2  р3
р3  …
…  рп+1. Число а яв-ся либо простым, либо составным. Но простым это число быть не может, т.к.оно больше любого из простых чисел р1, р2, р3, …, рп, а по предположению других простых чисел, кроме них, нет. Если бы а было составным числом, оно должно было бы иметь хотя бы один простой множитель, которым должно быть одно из чисел р1, р2, р3, …, рп. Но число а не делится ни на р1, ни на р2, ни на р3, …, ни на рп (при делении на любое из этих чисел всегда получается остаток 1). Значит, число а не составное. Противоречие показывает, что сделанное предположение неверное. Значит, множество простых чисел бесконечное. Метод Эратосфена (способ составления таблицы простых чисел, заключается в отсеивании составных чисел при последовательном вычеркивании чисел, делящихся на 2,3,5.): 1.Сначала выписывают все нат.числа от 2 до п. После этого вычёркиваются все числа, кратные 2, кроме числа 2 (вычёркивается каждое второе число, кроме 2). Пусть п=40. 2, 3
рп+1. Число а яв-ся либо простым, либо составным. Но простым это число быть не может, т.к.оно больше любого из простых чисел р1, р2, р3, …, рп, а по предположению других простых чисел, кроме них, нет. Если бы а было составным числом, оно должно было бы иметь хотя бы один простой множитель, которым должно быть одно из чисел р1, р2, р3, …, рп. Но число а не делится ни на р1, ни на р2, ни на р3, …, ни на рп (при делении на любое из этих чисел всегда получается остаток 1). Значит, число а не составное. Противоречие показывает, что сделанное предположение неверное. Значит, множество простых чисел бесконечное. Метод Эратосфена (способ составления таблицы простых чисел, заключается в отсеивании составных чисел при последовательном вычеркивании чисел, делящихся на 2,3,5.): 1.Сначала выписывают все нат.числа от 2 до п. После этого вычёркиваются все числа, кратные 2, кроме числа 2 (вычёркивается каждое второе число, кроме 2). Пусть п=40. 2, 3,4 , 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40. 2.Затем вычеркивают все числа, кратные 3, кроме 3 (каждое третье число, кроме 3). Оставшиеся числа не делятся ни на 2, ни на 3. 3.На следующем этапе вычёркивают числа, кратные 5. В результате останутся числа, которые не делятся ни на 2, ни на 3, ни на 5, кроме чисел 2, 3, 5. Если п=40, то 6 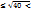 7. После того как вычеркнули числа, кратные 2, 3 и 5 (простые числа, меньше 7), в множестве остались только простые числа: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37.
7. После того как вычеркнули числа, кратные 2, 3 и 5 (простые числа, меньше 7), в множестве остались только простые числа: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37.
Измерение отрезков. Понятие о рациональной дроби. Свойства дробей.
Понятие дроби можно ввести на примере измерения длины отрезка. Пусть требуется измерить отрезок а с помощью отрезка е. Если отрезок е укладывается в отрезке а целое число (м) раз, то длина отрезка а=ме. Если же отрезок а несоизмерим с единичным отрезком е, то поступим следующим образом. Разделив единичный отрезок е на п равных частей, т.е.е=пе1. Пусть п-ая часть отрезка е поместилась в измеряемом отрезке м раз. Тогда длина отрезка а=ме1 или а=  Символ
Символ  называют обыкновенной дробью, где м,п- нат.числа. Число п называют знаменателем дроби. Знаменатель дроби показывает, на сколько равных частей разделили единичный элемент. Число м называют числителем дроби. Числитель показывает, сколько таких частей взяли. Две дроби
называют обыкновенной дробью, где м,п- нат.числа. Число п называют знаменателем дроби. Знаменатель дроби показывает, на сколько равных частей разделили единичный элемент. Число м называют числителем дроби. Числитель показывает, сколько таких частей взяли. Две дроби  и
и  называются равными, если выполняется условие: м=р и п=q. Две дроби
называются равными, если выполняется условие: м=р и п=q. Две дроби  и
и  называются эквивалентными, если мq=np, т.е.
называются эквивалентными, если мq=np, т.е. 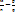
 mq=np. П: проверим, эквивалентны ли дроби
mq=np. П: проверим, эквивалентны ли дроби  и
и  . Дроби
. Дроби  и
и  не эквивалентны, т.к.произведение 19∙27
не эквивалентны, т.к.произведение 19∙27  23∙25. Теорема (основное свойство дроби): если числитель и знаменатель некоторой дроби умножить или разделить на одно и то же число не равное 0, то получим дробь эквивалентную данной. Док-во: умножим числитель и знаменатель дроби
23∙25. Теорема (основное свойство дроби): если числитель и знаменатель некоторой дроби умножить или разделить на одно и то же число не равное 0, то получим дробь эквивалентную данной. Док-во: умножим числитель и знаменатель дроби  на нат.число к, получим дробь
на нат.число к, получим дробь  . Покажем, что дроби
. Покажем, что дроби  и
и  эквивалентны. Найдём произведения м∙(пк) и п∙(мк). На основании ассоциативности умножения нат.чисел имеем: м∙(пк)=(мп) ∙к и п∙(мк)=(пм) ∙к= (мп) ∙к. Т.к.правые части равенств совпадают, то равны и левые части, т.е.дроби
эквивалентны. Найдём произведения м∙(пк) и п∙(мк). На основании ассоциативности умножения нат.чисел имеем: м∙(пк)=(мп) ∙к и п∙(мк)=(пм) ∙к= (мп) ∙к. Т.к.правые части равенств совпадают, то равны и левые части, т.е.дроби  и
и  эквивалентны. Покажем, что при делении числителя и знаменателя дроби на одно и то же число, не равное 0, также получаются эквивалентные дроби. Разделим числитель и знаменатель дроби
эквивалентны. Покажем, что при делении числителя и знаменателя дроби на одно и то же число, не равное 0, также получаются эквивалентные дроби. Разделим числитель и знаменатель дроби  на нат.число с, получим дробь
на нат.число с, получим дробь  . Покажем, что дроби
. Покажем, что дроби  и
и  эквивалентны. Найдём произведения числителя первой дроби на знаменатель второй и знаменателя первой дроби на числитель второй: м∙(п:с) и п∙(м:с). Согласно правилу умножения числа на частное будем иметь: м∙(п:с)= (м∙п):с и п∙(м:с)= (п∙м):с. Произведения равны, следовательно, дроби
эквивалентны. Найдём произведения числителя первой дроби на знаменатель второй и знаменателя первой дроби на числитель второй: м∙(п:с) и п∙(м:с). Согласно правилу умножения числа на частное будем иметь: м∙(п:с)= (м∙п):с и п∙(м:с)= (п∙м):с. Произведения равны, следовательно, дроби  и
и  эквивалентны. Умножение числителя и знаменателя дроби на одно и то же число применяют при сложении и вычитании дробей, приводя их к общему знаменателю. Приведение дробей к общему знаменателю- это замена дробей эквивалентными им дробями, имеющими одинаковые знаменатели. Чтобы привести дроби к наименьшему общему знаменателю, нужно: 1)найти НОК знаменателей данных дробей; 2)вычислить дополнительные множители, разделив НОК на каждый знаменатель; 3)умножить числитель и знаменатель каждой дроби на соответствующий дополнительный множитель.
эквивалентны. Умножение числителя и знаменателя дроби на одно и то же число применяют при сложении и вычитании дробей, приводя их к общему знаменателю. Приведение дробей к общему знаменателю- это замена дробей эквивалентными им дробями, имеющими одинаковые знаменатели. Чтобы привести дроби к наименьшему общему знаменателю, нужно: 1)найти НОК знаменателей данных дробей; 2)вычислить дополнительные множители, разделив НОК на каждый знаменатель; 3)умножить числитель и знаменатель каждой дроби на соответствующий дополнительный множитель.
Умножение и деление рациональных чисел. Законы сложения.
Произведением рациональных чисел  и
и  называется рациональное число
называется рациональное число  . Произведение рациональных чисел всегда существует и единственно. Теорема: Операция умножения рациональных чисел обладает коммутативным, ассоциативным и дистрибутивным свойствами, т.е.
. Произведение рациональных чисел всегда существует и единственно. Теорема: Операция умножения рациональных чисел обладает коммутативным, ассоциативным и дистрибутивным свойствами, т.е.
1.(  a,b
a,b 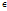 Q) a
Q) a 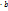 =b
=b  a коммутативность умножение ; 2.(
a коммутативность умножение ; 2.(  a,b,c
a,b,c  Q)(a
Q)(a  b)
b)  c = a
c = a  (b
(b  c) ассоциативность умножение ; 3.(
c) ассоциативность умножение ; 3.( 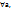 b,c
b,c  Q)(a+b)
Q)(a+b)  c=a
c=a 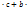 с дистрибутивность умножения . Законы: переместительный, сочетательный и распределительный. Частным рациональных чисел
с дистрибутивность умножения . Законы: переместительный, сочетательный и распределительный. Частным рациональных чисел  и
и  называется рациональное число
называется рациональное число  такое, что
такое, что 
 =
=  . Это значит, что
. Это значит, что  :
:  =
= 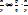 =
=  . Найдём значение дроби
. Найдём значение дроби  . По определению произведения дробей имеем:
. По определению произведения дробей имеем:  =
=  , т.е.
, т.е.  =
=  , отсюда (рх)
, отсюда (рх)  п= (qy)
п= (qy)  m. На основании коммутативности и ассоциативности умножения целых чисел будем иметь: х
m. На основании коммутативности и ассоциативности умножения целых чисел будем иметь: х  (рп)= у
(рп)= у  (qm). Отсюда получим:
(qm). Отсюда получим:  =
=  или
или  =
=  =
= 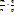 . Тогда деление дробей можно заменить умножением:
. Тогда деление дробей можно заменить умножением: 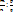 =
= 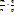 . Дробь
. Дробь  называется обратной дроби
называется обратной дроби  , если
, если  =1. Теорема: частное рациональных чисел
=1. Теорема: частное рациональных чисел  и
и  (р
(р  0) всегда существует и единственное. Справедливость этой теоремы вытекает из того, что р
0) всегда существует и единственное. Справедливость этой теоремы вытекает из того, что р  п
п  0, а mq- произведение целых чисел, которое всегда существует. Решение задач на части: 1)нахождение части от целого числа. Чтобы найти
0, а mq- произведение целых чисел, которое всегда существует. Решение задач на части: 1)нахождение части от целого числа. Чтобы найти  от числа а, достаточно, число а умножить на
от числа а, достаточно, число а умножить на  , т.е.а
, т.е.а  = а:п
= а:п  м. 2)нахождение целого числа по известной его части. Если
м. 2)нахождение целого числа по известной его части. Если  некоторого числа равны а, то, чтобы найти это число, достаточно а разделить на
некоторого числа равны а, то, чтобы найти это число, достаточно а разделить на  , т.е.а:
, т.е.а:  = (а:м)
= (а:м)  п.
п.
Приближённые значения положительного действительного числа. Сумма и разность положительных действительных чисел.
Приближённым значением положительного действительного числа по недостатку с точностью до 1/10п называют число, которое получается из данного числа, если отбросить все цифры, стоящие после п-го десятичного знака. Чтобы получить приближённое значение этого числа по избытку с точностью до 1/10п, надо увеличить на 1 последнюю цифру его приближённого значения по недостатку. Число х можно записать следующим образом: а0+а1/10+а2/102+…+ ап/10п  х
х  а0+а1/10+а2/102+…+ ап+1/10п, или а0,а1а2…ап
а0+а1/10+а2/102+…+ ап+1/10п, или а0,а1а2…ап 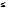 х
х  а0,а1а2…(а+1) или хп
а0,а1а2…(а+1) или хп 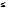 х
х  хп’, где хп- приближённое значение числа х по недостатку с точностью до 1/10п; хп’- прібліжённое значеніе чісла х по ізбытку с точностью до 1/10п. П: найдём прібліжённые значенія чісла
хп’, где хп- приближённое значение числа х по недостатку с точностью до 1/10п; хп’- прібліжённое значеніе чісла х по ізбытку с точностью до 1/10п. П: найдём прібліжённые значенія чісла 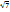 =2,64575… по недостатку і по ізбытку с точностью до 0,1; 0,01; 0,001. 2,6
=2,64575… по недостатку і по ізбытку с точностью до 0,1; 0,01; 0,001. 2,6 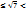 2,7 с точностью до 0,1; 2,64
2,7 с точностью до 0,1; 2,64 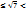 2,65 с точностью до 0,01; 2,645
2,65 с точностью до 0,01; 2,645 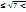 2,646 с точностью до 0,001. Пусть дана два положительных действительных числа х и у: х=а0,а1а2…ап… и у=в0,в1в2…вп….При любом п будем иметь неравенства: хп
2,646 с точностью до 0,001. Пусть дана два положительных действительных числа х и у: х=а0,а1а2…ап… и у=в0,в1в2…вп….При любом п будем иметь неравенства: хп 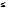 х
х  хп’, уп
хп’, уп 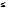 у
у  уп’. Суммойполож.действ.числа х и у называют число х+у, удовлетворяющее условию: хп+уп
уп’. Суммойполож.действ.числа х и у называют число х+у, удовлетворяющее условию: хп+уп 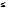 х+у
х+у  хп’+уп’, где хп и уп- десятичные приближённые значения этих чисел по недостатку, а хп’ и уп’- десятичные приближённые значения этих чисел по избытку. П: найдём сумму
хп’+уп’, где хп и уп- десятичные приближённые значения этих чисел по недостатку, а хп’ и уп’- десятичные приближённые значения этих чисел по избытку. П: найдём сумму 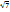 +0,(6) с точностью до 0,001.
+0,(6) с точностью до 0,001. 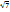 =2,645751…, 0,(6)=0,666666… Запишем данные числа с помощью приближённых значений по недостатку и по избытку с точностью до 0,0001 (для промежуточных вычислений берётся одна “запасная цифра”).
=2,645751…, 0,(6)=0,666666… Запишем данные числа с помощью приближённых значений по недостатку и по избытку с точностью до 0,0001 (для промежуточных вычислений берётся одна “запасная цифра”).
2,6457 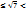 2,6458
2,6458
0,6666 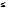 0,(6)
0,(6)  0,6667
0,6667
__________________________
3,3123 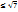 +0,(6)
+0,(6)  3,3125.
3,3125.
Значение суммы 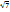 +0,(6) с точностью до 0,001 будет: 3,312
+0,(6) с точностью до 0,001 будет: 3,312 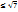 +0,(6)
+0,(6)  3,313.
3,313.
Операция сложения в мн.R+ полож.действ.чисел обладает св-ми коммутативности- (  х,у
х,у  R+)х+у= у+х и ассоциативности- (
R+)х+у= у+х и ассоциативности- (  х,у,z
х,у,z  R+) (х+у)+ z= х+(у+z). Разностью полож.действит.чисел х и у (х
R+) (х+у)+ z= х+(у+z). Разностью полож.действит.чисел х и у (х  у) называют действительное число z такое, что z+у=х, т.е.х-у= z
у) называют действительное число z такое, что z+у=х, т.е.х-у= z  z+у=х. Если задать числа х и у своими приближёнными значениями, то будем иметь: хп-уп’
z+у=х. Если задать числа х и у своими приближёнными значениями, то будем иметь: хп-уп’ 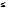 х-у
х-у  хп’-уп. Обоснуем это правило. Т.к.х-у=х+(-у), то, выполнив сложение чисел х и –у, получим:
хп’-уп. Обоснуем это правило. Т.к.х-у=х+(-у), то, выполнив сложение чисел х и –у, получим:
хп  хп’
хп’
-уп’ 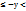 -уп
-уп
_____________________
хп-уп’  хп’-уп
хп’-уп
П: найдём разность 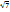 -0,(6) с точностью до 0,001.
-0,(6) с точностью до 0,001.
2,6457 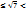 2,6458
2,6458
0,6666 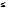 0,(6)
0,(6)  0,6667
0,6667
________________________
2,6457-0,6667 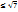 -0,(6)
-0,(6)  2,6458-06666
2,6458-06666
1,9790 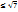 -0,(6)
-0,(6)  1,9792.
1,9792.
Значеніе разності 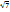 -0,(6) с точностью до 0,001 будет: 1,979
-0,(6) с точностью до 0,001 будет: 1,979 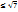 -0,(6)
-0,(6)  1,980.
1,980.
Произведение и частное положительных действительных чисел.
Произведением полож.действ.чисел х и у называется число х  у, удовлетворяющее неравенству: хп∙уп
у, удовлетворяющее неравенству: хп∙уп 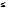 х∙у
х∙у  хп’∙уп’. П: найдём произведение
хп’∙уп’. П: найдём произведение 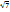 ∙0,(6) с точностью до 0,001.
∙0,(6) с точностью до 0,001.
2,6457 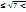 2,6458
2,6458
0,6666 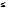 0,(6)
0,(6)  0,6667
0,6667
_____________________
1,7636 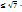 0,(6)
0,(6)  1,7639
1,7639
1,763 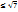 ∙0,(6)
∙0,(6)  1,764.
1,764.
Умножение полож.действ.чисел обладает св-ми коммутативности- (  х,у,
х,у,  R+)x∙y=y∙x; ассоциативности –(
R+)x∙y=y∙x; ассоциативности –(  х,у,z
х,у,z  R+)(x∙y) ∙z= x∙(y∙z); и дистрибутивности- (
R+)(x∙y) ∙z= x∙(y∙z); и дистрибутивности- (  х,у,z
х,у,z  R+)(x+y) ∙z= x∙z+y∙z. Деление полож.действ.чисел определяется как действие, обратное умножению: а:в=а∙
R+)(x+y) ∙z= x∙z+y∙z. Деление полож.действ.чисел определяется как действие, обратное умножению: а:в=а∙  . Частным полож.действ.чисел х и у называется число х:у, удовлетворяющее неравенству: хп:уп’
. Частным полож.действ.чисел х и у называется число х:у, удовлетворяющее неравенству: хп:уп’ 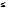 х:у
х:у  хп’:уп. П: найдём частное
хп’:уп. П: найдём частное 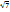 :0,(6) с точностью до 0,001. Запишем данные числа с помощью их рациональных приближений по недостатку и по избытку, взяв после запятой четыре десятичных знака (с запасной цифрой), и выполним указанное действие.
:0,(6) с точностью до 0,001. Запишем данные числа с помощью их рациональных приближений по недостатку и по избытку, взяв после запятой четыре десятичных знака (с запасной цифрой), и выполним указанное действие.
2,6457 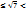 2,6458
2,6458
0,6666 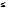 0,(6)
0,(6)  0,6667
0,6667
__________________________________
2,6457:0,6667 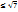 :0,(6)
:0,(6)  2,6458:0,6666
2,6458:0,6666
3,9683 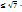 0,(6)
0,(6)  3,9690
3,9690
Значение частного 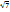 :0,(6) с точностью до 0,001 будет:
:0,(6) с точностью до 0,001 будет:
3,968 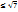 :0,(6)
:0,(6)  3,969. В мн.R+ полож.действ.чисел операция деления яв-ся всегда выполнимой операцией, кроме деления на 0.
3,969. В мн.R+ полож.действ.чисел операция деления яв-ся всегда выполнимой операцией, кроме деления на 0.
Понятие величины. Аксиоматическое определение величины.
Величина- это такое св-во предметов или явлений, которое позволяет их сравнивать и устанавливать пары объектов, обладающих этим св-ом в большей (меньшей) или в равной мере. П: длина, площадь, объём, температура, маса- св-ва предметов. Время, скорость, ускорение- св-ва явлений. Величины бывают скалярными и векторными. Величины, которые полностью определяются числовым значением, называются скалярными (длина, площадь, маса, температура, объём, время). Векторные величины хар-ся числовым значением и направлением (скорость, ускорение).Некоторые величины обладают свойством аддитивности- если предмет или явление могут состоять из частей, то величина целого складывается из величин отдельных частей, причём складываются только величины одного рода. Аксиоматическое определение величины:пусть М- мн.тех предметов или явлений, которые обладают св-ом А, и пусть для некоторых элементов мн.М определена операция сложения. Пусть во мн.М выбран элемент е 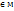 , называемый единицей измерения, и определено отношение эквивалентности а
, называемый единицей измерения, и определено отношение эквивалентности а 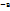 . Св-во А называется аддитивно-скалярной величиной, если существует отображение
. Св-во А называется аддитивно-скалярной величиной, если существует отображение  между мн.М и мн.полож.действ.чисел R+, которое удовлетворяет следующим условиям: 1.ʄ(е)=1. 2.если а и в- элементы мн.М, эквивалентные относительно св-ва А, то ʄ(а)=ʄ(в). 3.если во мн.М элементы а и в допускают сложение, т.е.а+в=с, то ʄ(а)+ʄ(в)=ʄ(с). 4.если во мн.М определены два отображения ʄ1 и ʄ2, которые удовлетворяют условиям 1-3, то существует такое положительное дейст.число k, что ʄ2(а)=k∙ʄ1(а). Отображение ʄ называют измерением величины А, положительные действительные числа ʄ(а), ʄ(в), ʄ(с) называются значениями величины А. Из 4 св-ва следуе вывод: пусть в некоторой системе измерения ʄ двум разным элементам а и в мн.М соответствует одно и то действ.число, т.е.ʄ(а)=ʄ(в). Рассмотрим другую систему измерения ʄ1, в которой элементу а соответствует число ʄ1(а), а элементу в- число ʄ1(в). Тогда существует положительное число k, что ʄ1(а)=k ∙ʄ(а), ʄ1(в)=k∙ʄ(в). Если обе части равенства ʄ(а)=ʄ(в) умножить на число k, то получим: k∙ʄ(а)=k∙ʄ(в), т.е.ʄ1(а)=ʄ1(в). Это значит, что если в некоторой системе измерения двум разным элементам а и в
между мн.М и мн.полож.действ.чисел R+, которое удовлетворяет следующим условиям: 1.ʄ(е)=1. 2.если а и в- элементы мн.М, эквивалентные относительно св-ва А, то ʄ(а)=ʄ(в). 3.если во мн.М элементы а и в допускают сложение, т.е.а+в=с, то ʄ(а)+ʄ(в)=ʄ(с). 4.если во мн.М определены два отображения ʄ1 и ʄ2, которые удовлетворяют условиям 1-3, то существует такое положительное дейст.число k, что ʄ2(а)=k∙ʄ1(а). Отображение ʄ называют измерением величины А, положительные действительные числа ʄ(а), ʄ(в), ʄ(с) называются значениями величины А. Из 4 св-ва следуе вывод: пусть в некоторой системе измерения ʄ двум разным элементам а и в мн.М соответствует одно и то действ.число, т.е.ʄ(а)=ʄ(в). Рассмотрим другую систему измерения ʄ1, в которой элементу а соответствует число ʄ1(а), а элементу в- число ʄ1(в). Тогда существует положительное число k, что ʄ1(а)=k ∙ʄ(а), ʄ1(в)=k∙ʄ(в). Если обе части равенства ʄ(а)=ʄ(в) умножить на число k, то получим: k∙ʄ(а)=k∙ʄ(в), т.е.ʄ1(а)=ʄ1(в). Это значит, что если в некоторой системе измерения двум разным элементам а и в 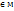 соответствует одно и то же число, то им будет соответствовать одно и то же число в любой системе измерения. Такие элементы называют равновеликими.
соответствует одно и то же число, то им будет соответствовать одно и то же число в любой системе измерения. Такие элементы называют равновеликими.
Измерение величины.
Измерение величин заключается в сравнении данной величины с другой величиной того же рода, принятой за единицу. Пусть дана величина а и выбрана единица величины е. Тогда в результате измерения величины а находят такое положительное действ.число х, что а=х∙е. Число х 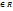 + называют значением величины а при единице измерения е: х=ʄ(а) или х=me(a). П: 9 кг=9∙1кг, 25 см=25∙1см. Такие рассуждения дают возможность обосновать процесс перехода от одной единицы измерения к другой. Пусть от единицы е требуется перейти к единице величины е1, причём, е=уе1 и а=хе, где х,у
+ называют значением величины а при единице измерения е: х=ʄ(а) или х=me(a). П: 9 кг=9∙1кг, 25 см=25∙1см. Такие рассуждения дают возможность обосновать процесс перехода от одной единицы измерения к другой. Пусть от единицы е требуется перейти к единице величины е1, причём, е=уе1 и а=хе, где х,у 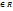 +. Тогда а=хе=х∙(уе1)=(х∙у)е1. П: 5ч=5∙1ч=5∙60мин= (5∙60)мин= 300 мин. Измерение величин позволяет свести сравнение величин к сравнению чисел, а операции над величинами- к операциям над числами. 1.Если величины а и в измерены с помощью одной и той же единицы е, то отношения между ними будут такие же, как и отношения между их числовыми значениями: а=в
+. Тогда а=хе=х∙(уе1)=(х∙у)е1. П: 5ч=5∙1ч=5∙60мин= (5∙60)мин= 300 мин. Измерение величин позволяет свести сравнение величин к сравнению чисел, а операции над величинами- к операциям над числами. 1.Если величины а и в измерены с помощью одной и той же единицы е, то отношения между ними будут такие же, как и отношения между их числовыми значениями: а=в  ʄ(а)=ʄ(в); а
ʄ(а)=ʄ(в); а 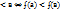 ; а
; а  . П: если массы двух тел а=5 кг и в=7 кг, то можно утверждать, что масса тела а меньше массы тела в, т.к.5
. П: если массы двух тел а=5 кг и в=7 кг, то можно утверждать, что масса тела а меньше массы тела в, т.к.5 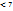 . 2.Если величины а и в измерены с помощью одной единицы величины е, то, чтобы найти числовое значение суммы а+в, достаточно сложить числовые значения величин а и в: если а+в=с, то ʄ(а+в)= ʄ(а)+ʄ(в). П: если а=20 кг, в=7кг, то а+в=20кг+7кг= (20+7)кг=27кг. 3.Если в=х∙а, где х
. 2.Если величины а и в измерены с помощью одной единицы величины е, то, чтобы найти числовое значение суммы а+в, достаточно сложить числовые значения величин а и в: если а+в=с, то ʄ(а+в)= ʄ(а)+ʄ(в). П: если а=20 кг, в=7кг, то а+в=20кг+7кг= (20+7)кг=27кг. 3.Если в=х∙а, где х 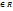 +, то, чтобы найти числовое значение величины в, достаточно число х умножить на числовое значение величины а, т.е.в=х∙а
+, то, чтобы найти числовое значение величины в, достаточно число х умножить на числовое значение величины а, т.е.в=х∙а  ʄ(в)= х∙ʄ(а). П: если масса тела в в 4 раза больше массы тела а, то в=4а. Если а=6кг, то в=4а= 4∙(6кг)= (4∙6)кг=24кг.
ʄ(в)= х∙ʄ(а). П: если масса тела в в 4 раза больше массы тела а, то в=4а. Если а=6кг, то в=4а= 4∙(6кг)= (4∙6)кг=24кг.
Аксиоматическое определение суммы натуральных чисел. Законы сложения. Таблица сложения
Сложением натуральных чисел называется алгебраическая операция, определённая на мн.N натуральных чисел, ставящая в соответствие каждой паре (а,b) число а+b, удовлетворяющее следующим св-ам:1. (∀ а є N) а + 1 = a' ; 2.(∀ a,b є N) а + b'= (а + b)'. Число а + b называется суммой чисел а и b, а сами числа а и b - слагаемыми. Теорема 1(о существовании и единственности суммы). Сложение натуральных чисел всегда существует и единственно. Док-во существования. В мн. N существует операция, удовлетворяющая аксиомам сложения. Для док-ва достаточно указать операцию, удовлетворяющую этим аксиомам. Докажем м.матем.индукции, что при а=1 и любом b сложение можно производить по правилу: 1+ b= b’. Пусть b=1, тогда 1+1=1’. Это значит, что выполняется аксиома 1 сложения. Предположим, что операция сложения, определённая по правилу 1+ b= b’, удовлетворяет свойствам сложения 1-2 для некоторого произвольного натурального числа b, т.е.предположим, что 1+ b= b’. Пользуясь предположением, докажем, что введённая операция удовлетворяет аксиомам сложения и для числа b’, т.е.докажем, что 1+ b’=( b’)’. Действительно, поскольку b’=1+ b, то 1+ b’=(1+ b)’ =( b’) ’. Из последнего равенства следует выполнимость второй аксиомы а+ b’=(а+ b)’ для произвольного числа b’ при а=1. Итак, существование алгебраической операции, удовлетворяющей свойствам 1 и 2, при а=1 доказано. Предположим, что для некоторого произвольного натурального числа а существует алгебраическая операция, удовлетворяющая свойствам сложения 1 и 2. Используя это предположение, докажем существование алгебраической операции для числа а ’, удовлетворяющей аксиомам сложения 1 и 2. Введём правило:1+ b= b’. Проверим выполнение аксиом сложения 1 и 2 м.матем.индукции. Пусть b=1, тогда а ’+1=(а+1) ’= (а ’) ’,т.е.а ’+1= (а ’) ’, а это означает выполнимость первой аксиомы для некоторого числа b. Пользуясь предположением, докажем, что введённая операция сложения удовлетворяет аксиоме 2 и для b’. Действительно, а ’+ b’= (а+ b’) ’= ((а+ b)’) ’= (а ’+ b)’, т.е.а ’+ b’= (а ’+ b)’, а это означает выполнимость второго св-ва сложения для а ’. Таким образом, доказано существование алгебраической операции, удовлетворяющей св-ам 1 и 2 для числа а ’.
На основании доказанного и принципа мат.индукции заключаем, что операция сложения натуральных чисел существует. Пользуясь определением операции сложения, можно составить таблицу сложения однозначных натуральных чисел. Таблицу составим в следующей последовательности: сначала рассмотрим прибавление единицы к любому однозначному нат.числу, затем –прибавление числа 2 , затем- прибавление числа 3 и т.д. а)1+1=1’=2, 2+1=2’=3, 3+1=3’=4, 4+1=4’=5 и т.д. б)1+2=1+1’= (1+1) ’=2’=3, 2+2=2+1’= (2+1) ’=3’=4, 3+2= 3+1’= (3+1) ’= 4’=5 и т.д.
Теорема 2. (∀ а,b,с є N) (а + b) + с = а + (b + с)-ассоциативнаДоказательство. Пусть натуральные числа a и b выбраны произвольно, а с принимает различные натуральные значения. Покажем, что при с=1 верно равенство (a+b)+1 = а+(b+1) .Действительно, по определе¬нию сложения, имеем (а + b) + 1 = (a + b)' = a+b' = a+(b+1). Предположим, что при некотором с верно равенство (а + b) + с = а+(b+с). На основании предположения докажем, что для числа с' выполняется равенство (а+b)+c'= a+(b+c'). (a+b)+c' = ((а+b)+с)' =( а+ (b +с)) '= a+(b+c) '= a+ (b+c'). на основании м.матем.индукции данное равенство верно для любого нат.числа с. Так как числа а и b были выбраны произвольно, то это равенство будет верно и для любых натуральных а и b.
Теорема 3. (∀ a,b є N) а + b = b + а.-коммуникативнаЗаконы сложения используются для упрощения вычислений. Для натуральных чисел есть два закона сложения: переместительный и сочетательный.Правило: От перемены мест слагаемых сумма не изменяется (переместительный закон сложения)- а + Ь = Ь + а. Правило. Чтобы к сумме двух слагаемых прибавить третье слагаемое, можно к первому слагаемому прибавить сумму второго и третьего слагаемых (сочетательный закон сложения)- (а + Ь) + с = а + (Ь + с).


 t, следовательно, t
t, следовательно, t  d. Надо доказать, что t=1. По св-ву транзитивности отношения делимости имеем: а
d. Надо доказать, что t=1. По св-ву транзитивности отношения делимости имеем: а 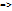 a
a 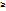 1. Если t
1. Если t  1, то t
1, то t  . Док-во: пусть а- составное число, а р- его наименьший простой делитель, тогда а=рв. При этом р
. Док-во: пусть а- составное число, а р- его наименьший простой делитель, тогда а=рв. При этом р 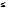 в. Умножим обе части неравенства на р. Получим р2
в. Умножим обе части неравенства на р. Получим р2  . Из этой теоремы следует, что если число а не делится ни на одно простое число, не превосходящее
. Из этой теоремы следует, что если число а не делится ни на одно простое число, не превосходящее 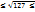 12. Мн.простых чисел, меньших 12, состоит из чисел 2,3,5,7,11. Т.к. 127 не делится ни на одно из этих простых чисел, то 127 само яв-ся простым числом.
12. Мн.простых чисел, меньших 12, состоит из чисел 2,3,5,7,11. Т.к. 127 не делится ни на одно из этих простых чисел, то 127 само яв-ся простым числом. р2
р2 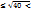 7. После того как вычеркнули числа, кратные 2, 3 и 5 (простые числа, меньше 7), в множестве остались только простые числа: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37.
7. После того как вычеркнули числа, кратные 2, 3 и 5 (простые числа, меньше 7), в множестве остались только простые числа: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37. Символ
Символ  называют обыкновенной дробью, где м,п- нат.числа. Число п называют знаменателем дроби. Знаменатель дроби показывает, на сколько равных частей разделили единичный элемент. Число м называют числителем дроби. Числитель показывает, сколько таких частей взяли. Две дроби
называют обыкновенной дробью, где м,п- нат.числа. Число п называют знаменателем дроби. Знаменатель дроби показывает, на сколько равных частей разделили единичный элемент. Число м называют числителем дроби. Числитель показывает, сколько таких частей взяли. Две дроби  называются равными, если выполняется условие: м=р и п=q. Две дроби
называются равными, если выполняется условие: м=р и п=q. Две дроби 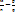
 mq=np. П: проверим, эквивалентны ли дроби
mq=np. П: проверим, эквивалентны ли дроби  и
и  . Дроби
. Дроби  23∙25. Теорема (основное свойство дроби): если числитель и знаменатель некоторой дроби умножить или разделить на одно и то же число не равное 0, то получим дробь эквивалентную данной. Док-во: умножим числитель и знаменатель дроби
23∙25. Теорема (основное свойство дроби): если числитель и знаменатель некоторой дроби умножить или разделить на одно и то же число не равное 0, то получим дробь эквивалентную данной. Док-во: умножим числитель и знаменатель дроби  . Покажем, что дроби
. Покажем, что дроби  . Покажем, что дроби
. Покажем, что дроби  называется рациональное число
называется рациональное число  . Произведение рациональных чисел всегда существует и единственно. Теорема: Операция умножения рациональных чисел обладает коммутативным, ассоциативным и дистрибутивным свойствами, т.е.
. Произведение рациональных чисел всегда существует и единственно. Теорема: Операция умножения рациональных чисел обладает коммутативным, ассоциативным и дистрибутивным свойствами, т.е. a,b
a,b 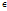 Q) a
Q) a 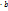 =b
=b  a коммутативность умножение ; 2.(
a коммутативность умножение ; 2.(  Q)(a
Q)(a  c) ассоциативность умножение ; 3.(
c) ассоциативность умножение ; 3.( 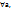 b,c
b,c  Q)(a+b)
Q)(a+b) 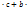 с дистрибутивность умножения . Законы: переместительный, сочетательный и распределительный. Частным рациональных чисел
с дистрибутивность умножения . Законы: переместительный, сочетательный и распределительный. Частным рациональных чисел  и
и  такое, что
такое, что  =
= 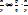 =
=  =
=  , т.е.
, т.е.  =
=  или
или  =
= 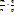 . Тогда деление дробей можно заменить умножением:
. Тогда деление дробей можно заменить умножением: 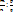 =
=  называется обратной дроби
называется обратной дроби  =1. Теорема: частное рациональных чисел
=1. Теорема: частное рациональных чисел  = а:п
= а:п 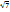 =2,64575… по недостатку і по ізбытку с точностью до 0,1; 0,01; 0,001. 2,6
=2,64575… по недостатку і по ізбытку с точностью до 0,1; 0,01; 0,001. 2,6 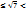 2,7 с точностью до 0,1; 2,64
2,7 с точностью до 0,1; 2,64 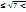 2,646 с точностью до 0,001. Пусть дана два положительных действительных числа х и у: х=а0,а1а2…ап… и у=в0,в1в2…вп….При любом п будем иметь неравенства: хп
2,646 с точностью до 0,001. Пусть дана два положительных действительных числа х и у: х=а0,а1а2…ап… и у=в0,в1в2…вп….При любом п будем иметь неравенства: хп 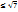 +0,(6)
+0,(6)  R+)х+у= у+х и ассоциативности- (
R+)х+у= у+х и ассоциативности- (  хп’
хп’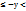 -уп
-уп хп’-уп
хп’-уп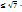 0,(6)
0,(6)  . Частным полож.действ.чисел х и у называется число х:у, удовлетворяющее неравенству: хп:уп’
. Частным полож.действ.чисел х и у называется число х:у, удовлетворяющее неравенству: хп:уп’ 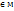 , называемый единицей измерения, и определено отношение эквивалентности а
, называемый единицей измерения, и определено отношение эквивалентности а 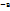 . Св-во А называется аддитивно-скалярной величиной, если существует отображение
. Св-во А называется аддитивно-скалярной величиной, если существует отображение  между мн.М и мн.полож.действ.чисел R+, которое удовлетворяет следующим условиям: 1.ʄ(е)=1. 2.если а и в- элементы мн.М, эквивалентные относительно св-ва А, то ʄ(а)=ʄ(в). 3.если во мн.М элементы а и в допускают сложение, т.е.а+в=с, то ʄ(а)+ʄ(в)=ʄ(с). 4.если во мн.М определены два отображения ʄ1 и ʄ2, которые удовлетворяют условиям 1-3, то существует такое положительное дейст.число k, что ʄ2(а)=k∙ʄ1(а). Отображение ʄ называют измерением величины А, положительные действительные числа ʄ(а), ʄ(в), ʄ(с) называются значениями величины А. Из 4 св-ва следуе вывод: пусть в некоторой системе измерения ʄ двум разным элементам а и в мн.М соответствует одно и то действ.число, т.е.ʄ(а)=ʄ(в). Рассмотрим другую систему измерения ʄ1, в которой элементу а соответствует число ʄ1(а), а элементу в- число ʄ1(в). Тогда существует положительное число k, что ʄ1(а)=k ∙ʄ(а), ʄ1(в)=k∙ʄ(в). Если обе части равенства ʄ(а)=ʄ(в) умножить на число k, то получим: k∙ʄ(а)=k∙ʄ(в), т.е.ʄ1(а)=ʄ1(в). Это значит, что если в некоторой системе измерения двум разным элементам а и в
между мн.М и мн.полож.действ.чисел R+, которое удовлетворяет следующим условиям: 1.ʄ(е)=1. 2.если а и в- элементы мн.М, эквивалентные относительно св-ва А, то ʄ(а)=ʄ(в). 3.если во мн.М элементы а и в допускают сложение, т.е.а+в=с, то ʄ(а)+ʄ(в)=ʄ(с). 4.если во мн.М определены два отображения ʄ1 и ʄ2, которые удовлетворяют условиям 1-3, то существует такое положительное дейст.число k, что ʄ2(а)=k∙ʄ1(а). Отображение ʄ называют измерением величины А, положительные действительные числа ʄ(а), ʄ(в), ʄ(с) называются значениями величины А. Из 4 св-ва следуе вывод: пусть в некоторой системе измерения ʄ двум разным элементам а и в мн.М соответствует одно и то действ.число, т.е.ʄ(а)=ʄ(в). Рассмотрим другую систему измерения ʄ1, в которой элементу а соответствует число ʄ1(а), а элементу в- число ʄ1(в). Тогда существует положительное число k, что ʄ1(а)=k ∙ʄ(а), ʄ1(в)=k∙ʄ(в). Если обе части равенства ʄ(а)=ʄ(в) умножить на число k, то получим: k∙ʄ(а)=k∙ʄ(в), т.е.ʄ1(а)=ʄ1(в). Это значит, что если в некоторой системе измерения двум разным элементам а и в 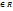 + называют значением величины а при единице измерения е: х=ʄ(а) или х=me(a). П: 9 кг=9∙1кг, 25 см=25∙1см. Такие рассуждения дают возможность обосновать процесс перехода от одной единицы измерения к другой. Пусть от единицы е требуется перейти к единице величины е1, причём, е=уе1 и а=хе, где х,у
+ называют значением величины а при единице измерения е: х=ʄ(а) или х=me(a). П: 9 кг=9∙1кг, 25 см=25∙1см. Такие рассуждения дают возможность обосновать процесс перехода от одной единицы измерения к другой. Пусть от единицы е требуется перейти к единице величины е1, причём, е=уе1 и а=хе, где х,у 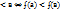 ; а
; а  . П: если массы двух тел а=5 кг и в=7 кг, то можно утверждать, что масса тела а меньше массы тела в, т.к.5
. П: если массы двух тел а=5 кг и в=7 кг, то можно утверждать, что масса тела а меньше массы тела в, т.к.5 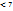 . 2.Если величины а и в измерены с помощью одной единицы величины е, то, чтобы найти числовое значение суммы а+в, достаточно сложить числовые значения величин а и в: если а+в=с, то ʄ(а+в)= ʄ(а)+ʄ(в). П: если а=20 кг, в=7кг, то а+в=20кг+7кг= (20+7)кг=27кг. 3.Если в=х∙а, где х
. 2.Если величины а и в измерены с помощью одной единицы величины е, то, чтобы найти числовое значение суммы а+в, достаточно сложить числовые значения величин а и в: если а+в=с, то ʄ(а+в)= ʄ(а)+ʄ(в). П: если а=20 кг, в=7кг, то а+в=20кг+7кг= (20+7)кг=27кг. 3.Если в=х∙а, где х