Уявна поверхня, всі точки якої мають однаковий потенціал називаються еквіпотенціальними поверхнями. Їх рівняння мають вигляд:
φ(x, y ,z)=const.
При переміщенні по еквіпотенціальній поверхні на dl потенціал φ не змінюється (dφ=0). Тоді дотична до поверхні складова вектора напруженості дорівнює нулю. Отже, вектор напруженості в кожній точці направлений по нормалі до еквіпотенціальної поверхні, яка проходить через дану точку. Звідси, лінії напруженості в кожній точці ортогональні до еквіпотенціальної поверхні.
Еквіпотенціальну поверхню можна провести через будь-яку точку поля, тоді таких поверхонь може бути безліч. Проводять такі поверхні таким чином, щоб різниця потенціалів для двох сусідніх поверхонь була всюди одна і та ж сама. В такому випадку, по густині еквіпотенціальних поверхонь можна судити про величину напруженості поля. Чим густіше розташовані еквіпотенціальні поверхні, тим швидше змінюється потенціал при переміщенні вздовж нормалі до поверхні, відповідно, тим більше в даному місці 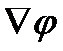 і Е.
і Е.
 Для однорідного поля еквіпотенціальні поверхні представляють собою систему рівновіддалених одна від одної площин, перпендикулярних до напрямку поля.
Для однорідного поля еквіпотенціальні поверхні представляють собою систему рівновіддалених одна від одної площин, перпендикулярних до напрямку поля.
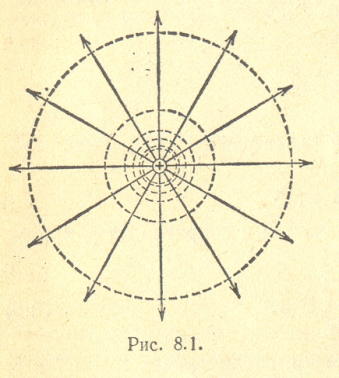
Для точкового заряду еквіпотенціальні поверхні можна представити у вигляді, показаному на рис.1.5.
Рис.1.6
1.7. Електричний диполь
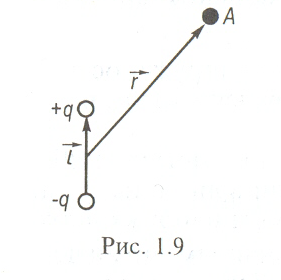
Електричним диполем називається система двох однакових за величиною різнойменних точкових зарядів +q і –q, відстань l між якими значно менша відстані до тих точок, в яких визначається поле системи. Пряма, яка проходить через обидва заряди називається віссю диполя; l – плече диполя.
Поле диполя має осьову симетрію. Якщо відстань між зарядами не змінюється, то такий диполь називається жорстким. Якщо довжина плеча диполя l мала порівняно з відстанню r до точки спостереження, то такий диполь називається точковим.
 Основною характеристикою електричного диполя є його електричний дипольний момент р – вектор, який чисельно дорівнює добуткові заряду на плече і направлений від негативного заряду до позитивного.
Основною характеристикою електричного диполя є його електричний дипольний момент р – вектор, який чисельно дорівнює добуткові заряду на плече і направлений від негативного заряду до позитивного.
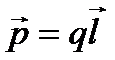 .
.
Рис.1.7


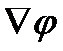 і Е.
і Е. Для однорідного поля еквіпотенціальні поверхні представляють собою систему рівновіддалених одна від одної площин, перпендикулярних до напрямку поля.
Для однорідного поля еквіпотенціальні поверхні представляють собою систему рівновіддалених одна від одної площин, перпендикулярних до напрямку поля. Основною характеристикою електричного диполя є його електричний дипольний момент р – вектор, який чисельно дорівнює добуткові заряду на плече і направлений від негативного заряду до позитивного.
Основною характеристикою електричного диполя є його електричний дипольний момент р – вектор, який чисельно дорівнює добуткові заряду на плече і направлений від негативного заряду до позитивного.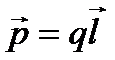 .
.