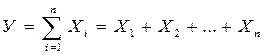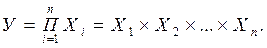Системний підхід в економічному аналізі викликає необхідність взаємозалежного вивчення факторів з урахуванням їх внутрішніх і зовнішніх зв’язків, взаємодії та взаємопідпорядкованості, що досягається за допомогою їх систематизації шляхом створення факторних систем.
Факторна система – це сукупність результативного та факторних показників, пов’язаних одним причиново-наслідковим зв’язком. Математична формула, що виражає реальні зв’язки між досліджуваними явищами, називається моделлю факторної системи:
у = f (х1, х2, ..., хп) , (4.2)
де у – результативний показник;
х1, х2, ..., хп – факторні показники.
Використання моделей в аналізі дає змогу абстрактно зобразити основні взаємозв’язки, що існують у реальній господарській системі.
Процес побудови аналітичного виразу причинно-наслідкової залежності називається процесом моделювання явища, що вивчається. Моделювання – це один із методів наукового пізнання, за допомогою якого створюється модель об’єкта дослідження. Сутність його полягає в тому, що взаємозв’язок показника, який досліджується, з факторними показниками подається у формі конкретного математичного рівняння.
Залежно від форми зв’язку між результативним і факторними показниками факторні моделі поділяються на дві групи:
1. Детерміновані факторні моделі –використовуються для дослідження функціонального (детермінованого) зв’язку між результативним і факторними показниками, коли при заданих початкових умовах факторна система переходить у єдиний певний стан. У детермінованих моделях результативний показник являє собою алгебраїчну суму, добуток або частку факторних показників.
2. Стохастичні факторні моделі – використовуються для дослідження ймовірносного (стохастичного) зв’язку між результативним і факторними показниками, коли при незмінних початкових умовах факторна система може переходити в різні стани з різною ймовірністю.
В економічному аналізі об’єктом поглибленого вивчення є детерміновані факторні моделі. Стохастичні ж моделі (кореляційно-регресійні, дисперсійні) вивчаються в курсі статистики.
При моделюванні детермінованих факторних систем необхідно дотримуватись таких вимог:
1. Фактори, що включаються в модель, і сама модель повинні мати чітко виражений характер, реально існувати, а не бути вигаданими абстрактними величинами або явищами.
2. Фактори, які входять у систему, мають не тільки бути необхідними елементами формули, а й знаходитися в причиновому зв’язку з результативним показником. Інакше кажучи, побудована факторна система повинна мати пізнавальну цінність. Розглянемо приклад двох моделей:
ВП = ЧП х ПП , (4.3)
ПП = ВП ¸ ЧП , (4.4)
де ВП – вартість продукції;
ЧП – середньорічна чисельність працівників;
ПП – продуктивність праці (обсяг виробництва продукції на
одного середньорічного працівника).
У першій моделі фактори перебувають у причиновому зв’язку з результативним показником, а в другій – у математичному співвідношенні.
3. Усі показники факторної моделі повинні бути кількісно вимірними, тобто мати одиницю величини і необхідну інформаційну забезпеченість.
4. Факторна модель має забезпечувати можливість вимірювання впливу окремих факторів на зміну результативного показника.
У детермінованому факторному аналізі використовуються чотири види факторних моделей:
1. Адитивні – моделі, в яких результативний показник є алгебраїчною сумою декількох факторних показників:
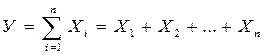
. (4.5)
Прикладами адитивних моделей можуть бути будь-які балансові моделі, зокрема факторні моделі валюти балансу:
А = А І + А ІІ + А ІІІ ; (4.6)
П = П І + П ІІ + П ІІІ + П ІV + П V , (4.7)
де А, П – валюта балансу, тобто підсумок відповідно активу і
пасиву;
А І, А ІІ, А ІІІ – підсумки відповідних розділів активу;
П І, П ІІ, П ІІІ, П ІV, П V – підсумки відповідних розділів
пасиву.
2. Мультиплікативні – моделі, в яких результативний показник є добутком декількох факторних показників:
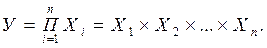
. (4.8)
Наприклад, факторна модель виручки від реалізації продукції:
В = q х р , (4.9)
де В – виручка;
q – обсяг реалізації;
р – ціна продукції.
Деталізація, або глибина, факторного аналізу багато в чому визначається числом факторів, тому велике значення в аналізі мають багатофакторні мультиплікативні моделі. В основі побудови цих моделей лежать наступні принципи:
- місце кожного фактора в моделі повинно відповідати його ролі у формуванні результативного показника;
- модель слід будувати з двофакторної повної моделі шляхом послідовного розподілу факторів (як правило, якісних) на складові. Наприклад, згідно з рисунком 6.1 детермінована факторна модель валової продукції може бути дво-, три- і чотирифакторною:
ВП = ЧП х РВ = ЧП х Д х ДВ = ЧП х Д х Т х ГВ ; (4.10)
- при написанні формули багатофакторної моделі фактори рекомендується розташовувати від кількісних до якісних з урахуванням порядку дії (спочатку фактори першого рівня, потім другого і т.д.).
3. Кратні – моделі, в яких результативний показник визначається діленням одного факторного показника на інший:
У = Х1 ¸ Х2 . (4.11)
Наприклад, факторна модель рівня рентабельності
РР = П ¸ С х 100 , (4.12)
де РР – рівень рентабельності, %;
П – прибуток від реалізації;
С – собівартість реалізованої продукції.
Якщо інші види детермінованих факторних моделей можуть уключати два, три і більшу кількість факторів, то кратні моделі є тільки двофакторними.
4. Змішані (комбіновані) – моделі, в яких поєднуються в різноманітних комбінаціях адитивна, мультиплікативна та кратна залежності:
У = А х (В – С); У = А ¸ (В + С);
У = (А + В) ¸ С; У = А х В ¸ С.