Вимірюючи будь-яку фізичну величину, не можна визначити дійсне її значення (навіть при ідеальному виключенні систематичних похибок) із-за неминучої появи в деяких результатах виміру малих відхилень, що змінюються по знаку і абсолютному значенню випадковим чином. Ці малі відхилення, що викликаються дією багаточисельних зовнішніх чинників, вплив яких практично врахувати неможливо, в метрології називають випадковими похибками. Абсолютні значення і знак цих похибок підкоряються імовірнісним законам.
При обробці результатів виміру безперервних фізичних величин найчастіше використовують нормальний закон розподілу щільності вірогідності (закон Гауса), який записують у вигляді співвідношення
 (5.21)
(5.21)
де δ -значення випадкової похибки; 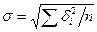 – середньоквадратичне відхилення декількох вимірів; п –число вимірів; у –щільність вірогідності для певного значення δ.
– середньоквадратичне відхилення декількох вимірів; п –число вимірів; у –щільність вірогідності для певного значення δ.
Як бачимо, у швидко убуває із збільшенням δ. Так, похибка δ > 4σз'являється лише один раз на 15625 вимірів, тобто дуже великі похибки маловірогідні; похибка δ > 3σ з'являється один раз на 370 вимірів, а похибка δ > 2σ – один раз на 22 виміри.
У теоретичному рівнянні (5.21) значення δ, рівне різниці між результатом одного виміру і дійсним значенням вимірюваної величини х, невідомо, оскільки безпосередньо визначити дійсне значення х неможливо. З цієї ж причини не можна підрахувати і σ. Тому для використання рівняння (5.21) потрібно прийняти якесь припущення про дійсне значення вимірюваної величини.
У літературі по теорії обробки результатів спостережень для усунення невизначеності значень δ і σ рекомендується за найбільш вірогідне значення вимірюваної величини х приймати таке її значення L, при якому сума квадратів абсолютних погрішностей мінімальна.
Нехай проведено п вимірів величини х і набуті значень l1, l2, l3, …, ln. Тоді вирази для окремих абсолютних погрішностей в припущенні, що систематичні погрішності виключені, запишуться так:
δ1 = l1 – x; δ2 = l2 – x; …; δn = ln – x (5.22)
Склавши вирази для суми δi і прирівнявши до нуля його першу похідну по х, отримаємо вираз для L як найбільш вірогідного значення х:
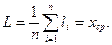 (5.23)
(5.23)
Таким чином, найбільш вірогідним значенням вимірюваної величини буде середньоарифметичне декількох її вимірів. Тому термін «випадкова похибка», замінюють терміном «випадкове відхилення», під яким розуміють різницю:
ρi = li – хср. (5.24)
При чималому числі вимірів середньоарифметичне прагне до дійсного значення вимірюваної величини, а випадкові відхилення ρi – до відповідних випадкових похибок δi.
Тепер для визначення точності п вимірів обчислюють оцінку S значення σ по відомій формулі Бесселя:
 (5.25)
(5.25)
Зрештою серії вимірів має бути отримане число, що визначає значення вимірюваної величини, і вказана міра його достовірності, тобто має бути отриманий результат виміру. Але в цій серії з n спостережень середньоарифметичне xср - лінійна функція результатів окремих спостережень l1, l2, …, ln. Якщо ж провести нову серію з п спостережень, то із-за впливу випадкових причин значення U відрізнятимуться від отриманих в першій серії. Отже, і нове значення хср буде іншим. Таким чином, число хср, отримане в одній серії спостережень, є випадковим наближенням до дійсного значення х. Тому аби мати уявлення про можливі відхилення хср від дійсного значення х, потрібно визначити його середньо квадратичного відхилення.
Оскільки результати окремих вимірів є взаимозалежними випадковими величинами, та використаня теореми про дисперсію D лінійної функції таких величин дозволяє записати:
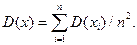 (5.26)
(5.26)
Рівноточність декількох вимірів передбачає рівність всіх окремих D(xi) = σ2 ≈ S2. Отже,
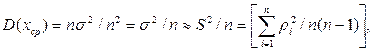 (5.27)
(5.27)
а тоді оцінка Δ° середньоквадратичної погрішності хср, тобто результату виміру:
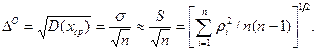 (5.28)
(5.28)
По визначених таким чином значеннях хср и Δ° можна записати і кінцевий результат виміру формою, рекомендованою ГОСТ 8.011-72: L; Δ; від Δн до Δв; Рд, де L - результат виміру в одиницях вимірюваної величини х, рівний xср; Δ, Δн, Δв - відповідно похибка виміру, нижняя і верхня її межі (межі довірчого інтервалу); Рд- встановлена вірогідність, з якою похибка виміру знаходиться в межах цих інтервалів (довірча вірогідність):
Рд= Р [(xср — Δн) < x < (xср + Δв)]. (5.29)
Величини Δн і Δв найчастіше мають однакові значення, і залежно від встановленої Рдїх приймають рівними Δ°, 2Δ° або ЗΔ°. Результати окремих спостережень, що виходять за межі довірчого інтервалу, відносять до промахів.
Всі перераховані співвідношення справедливі лише стосовно рівноточних вимірів. Проте часто доводиться визначати значення вимірюваної величини по декількох результатах вимірів різної точності, наприклад виконаних за допомогою різних приладів. Тоді за найбільш вірогідне значення вимірюваної величини слід приймати средньозважене:
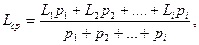 (5.30)
(5.30)
де Li - окремі виміри; pi - їх ваги, що є мірою довіри до кожного результату виміру.
Вибирати значення pi можна різними способами. Найчастіше критерієм служить значення средньоквадратичного відхилення. В цьому випадку ваги pi встановлюють обернено пропорційно до квадратів відхилень. Можна за критерій прийняти чутливість приладу або методу. Наприклад, якщо чутливість одного приладу удвічі вища іншего, то вазі результату виміру першим приладом p1 надається удвічі більше значення, чим p2.


 (5.21)
(5.21)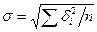 – середньоквадратичне відхилення декількох вимірів; п –число вимірів; у –щільність вірогідності для певного значення δ.
– середньоквадратичне відхилення декількох вимірів; п –число вимірів; у –щільність вірогідності для певного значення δ. 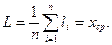 (5.23)
(5.23) (5.25)
(5.25)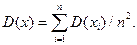 (5.26)
(5.26)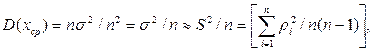 (5.27)
(5.27)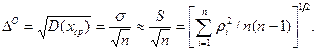 (5.28)
(5.28)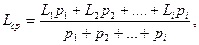 (5.30)
(5.30)