“Логічний” алгоритм утворення прямого коду для будь-яких цілих чисел А із знаком визначають за таким правилом:
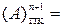 S
S 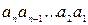 , ( 1.1 )
, ( 1.1 )
де 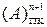 - прямий код (ПК) цілих чисел А за (n + 1)–розрядним форматом;
- прямий код (ПК) цілих чисел А за (n + 1)–розрядним форматом;
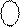
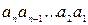 =
= 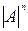 - цифрова частина (модуль) чисел А за n-розрядним форматом;
- цифрова частина (модуль) чисел А за n-розрядним форматом;
S - позначення знакового розряду прямого коду, в якому за традицією символ «+» шифрується цифрою 0, а символ «-» - цифрою 1.
Розглянемо типові приклади кодування чисел у прямих кодах за формулою (1.1).
Нехай А = - 101. Тоді згідно з ( 1.1 ) за чотирирозрядним форматом зображення числа А у прямому коді буде подано у такому вигляді:
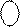
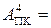 1 101.
1 101.
Нехай тепер В = +10. Тоді згідно з ( 1.1 ) машинне зображення такого додатного числа за чотирирозрядним форматом буде визначатися рядком цифр:
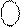
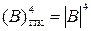 = 0 010,
= 0 010,
де |В|4 = 0010 - чотирипозиційне зображення модуля цілого числа В(|В|=10).
 Приклади подання чисел за таким способом у діапазоні зміни чисел від (-111) до (+111) наведено на рис.1.1. Слід звернути увагу на неоднозначність зображення нуля у прямому коді (рис.1.1). Нульовий результат у прямому коді подається двома комбінаціями:
Приклади подання чисел за таким способом у діапазоні зміни чисел від (-111) до (+111) наведено на рис.1.1. Слід звернути увагу на неоднозначність зображення нуля у прямому коді (рис.1.1). Нульовий результат у прямому коді подається двома комбінаціями: 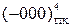 = 1 000,
= 1 000, 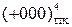 = 0 000. Отже, у прямих кодах множина додатних чисел включає як значущі додатні числа, так і ( +0 ), а множина від’ємних чисел - як значущі від’ємні числа, так і ( -0 ).
= 0 000. Отже, у прямих кодах множина додатних чисел включає як значущі додатні числа, так і ( +0 ), а множина від’ємних чисел - як значущі від’ємні числа, так і ( -0 ).
“Арифметичний” спосіб обчислення прямих кодів, наприклад, за чотирипозиційним форматом, визначається співвідношенням:
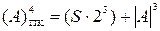 , ( 1.2 )
, ( 1.2 )
де (23)=810 – вага знакового розряду S у чотирирозрядному форматі прямомого коду;
| А |3 – цифрова частина (модуль) чисел А за трипозиційним форматом.
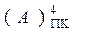 ( А ≤ - 0)
( А ≤ - 0)
| | | | |
| |  |
| | |  ( А ≥+0) ( А ≥+0)
| |
| |

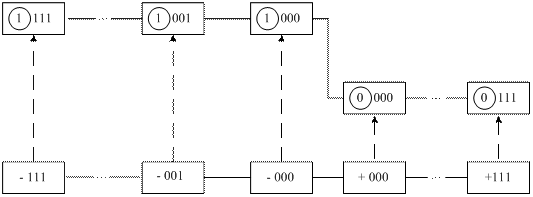
Рисунок 1.1 - Приклади комп’ютерного подання цілих
 чисел А = ±а3 а2 а1 у прямих кодах А
чисел А = ±а3 а2 а1 у прямих кодах А  = S а3 а2 а1:
= S а3 а2 а1:
а3 а2 а1 – трирозрядний формат цифрової частини чисел А;
S – знак числа у прямому коді
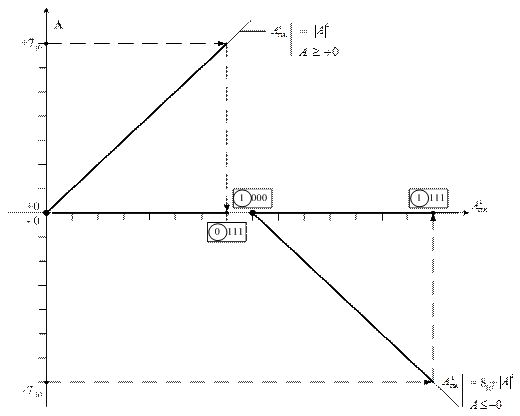
Рисунок 1.2 – Взаємозалежність між цілими числами А
із знаком та їх поданням у прямих кодах
Таким чином, згідно з (1.2) прямий код, наприклад, числа А = -101 можна побудувати за формулою:
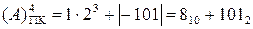 =10002+1012 = 1 101 .
=10002+1012 = 1 101 .
Для додатних чисел знак числа у прямих кодах зображується двійковою цифрою S = 0, тому, наприклад, обчислення зображення числа В=+112 у прямому коді за формулою (1.2) виконується наступним чином:
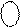
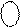
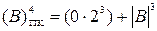 = 0
= 0 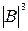 = 0 011.
= 0 011.
У графічній формі залежність ( 1.2 ) у діапазоні зміни аргументу від (-7)10 до ( +7 )10 подано на рис. 1.2.
1.1.2 Комп’ютерне подання чисел із знаком у доповняльних та


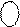
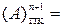 S
S 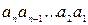 , ( 1.1 )
, ( 1.1 )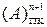 - прямий код (ПК) цілих чисел А за (n + 1)–розрядним форматом;
- прямий код (ПК) цілих чисел А за (n + 1)–розрядним форматом;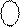
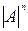 - цифрова частина (модуль) чисел А за n-розрядним форматом;
- цифрова частина (модуль) чисел А за n-розрядним форматом;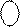
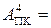 1 101.
1 101.
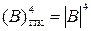 = 0 010,
= 0 010,
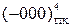 = 1 000,
= 1 000, 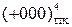 = 0 000. Отже, у прямих кодах множина додатних чисел включає як значущі додатні числа, так і ( +0 ), а множина від’ємних чисел - як значущі від’ємні числа, так і ( -0 ).
= 0 000. Отже, у прямих кодах множина додатних чисел включає як значущі додатні числа, так і ( +0 ), а множина від’ємних чисел - як значущі від’ємні числа, так і ( -0 ).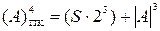 , ( 1.2 )
, ( 1.2 )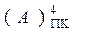 ( А ≤ - 0)
( А ≤ - 0)
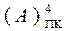 ( А ≥+0)
( А ≥+0)


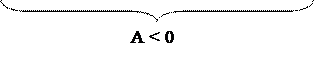
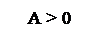
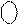 чисел А = ±а3 а2 а1 у прямих кодах А
чисел А = ±а3 а2 а1 у прямих кодах А  = S а3 а2 а1:
= S а3 а2 а1:
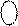
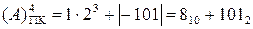 =10002+1012 = 1 101 .
=10002+1012 = 1 101 .
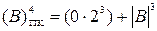 = 0
= 0 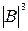 = 0 011.
= 0 011.