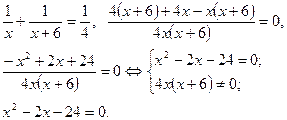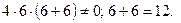Дробове раціональне рівняння це рівняння, у якого ліва або права частина і обидві — дробові вирази. Для його розв’язання доцільно виконати такі дії:
1) перенести всі доданки в один бік;
2) звести їх до спільного знаменника;
3)до одержаного рівняння виду 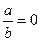 (де а і b — деякі цілі вирази) застосувати умову рівності дробу нулю;
(де а і b — деякі цілі вирази) застосувати умову рівності дробу нулю;
4) знайти корені чисельника;
5) перевірити, чи не дорівнює знаменник нулю при цих значеннях невідомого;
6) записати відповідь.
Приклад
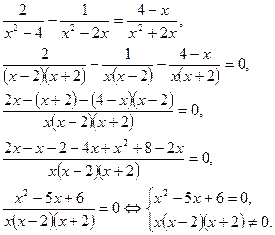
Дріб дорівнює нулю тоді й тільки тоді, коли чисельник дорівнює нулю, а знаменник відмінний від нуля:
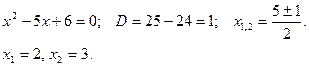
Якщо х = 2, то 2(2 – 2)(2 + 2) = 0.
Якщо х = 3,то 3(3 – 2)(3 + 2) ≠ 0.
Відповідь: х = 3.
Приклад
Розв’язати дробово-раціональне рівняння 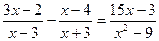 .
.
Розв’язання. 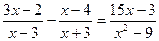 , ОДЗ:
, ОДЗ: 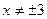
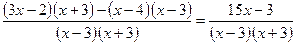
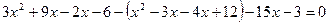
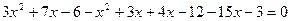 ,
, 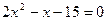
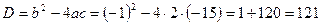
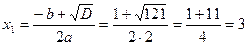 – сторонній корінь, тому що не задовольняє вимогам ОДЗ.
– сторонній корінь, тому що не задовольняє вимогам ОДЗ. 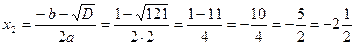
Відповідь. 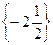 .
.
Приклад
Розв’язати дробово-раціональне рівняння 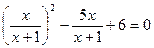 .
.
Розв’язання. 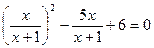 , ОДЗ:
, ОДЗ: 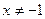 ,
, 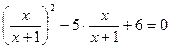 . Введемо заміну:
. Введемо заміну: 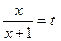 ,
, 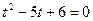 . За теоремою Вієта
. За теоремою Вієта 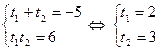
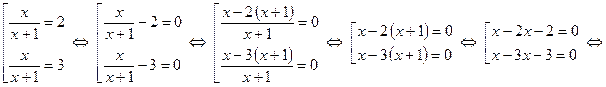
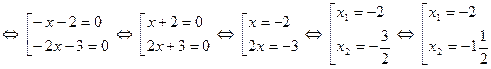
Відповідь. 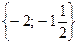 .
.
До дробових раціональних рівнянь приводить велика кількість задач на рух та спільну роботу.
Приклади
Задача 1 (на рух). Теплохід пройшов течією річки 150 км і повернувся назад, витративши на весь шлях 5,5 години. Знайдіть швидкість течії річки, якщо швидкість теплохода в стоячій воді 55 км/год.
Розв'язання
| Рух
| Швидкість (км/год)
| Час (год)
| Відстань (км)
|
| За течією
| (55+x)
| 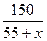
|
|
| Проти течії
| (55–x)
| 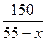
|
|
Нехай швидкість течії річки х км/год. Тоді за течією теплохід рухався зі швидкістю (55 + х) км/год і пройшов 150 км за 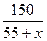 год. Проти течії теплохід рухався зі швидкістю (55–x) км/год і пройшов 150 км за
год. Проти течії теплохід рухався зі швидкістю (55–x) км/год і пройшов 150 км за 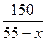 год. За умовою задачі, на весь шлях він витратив 5,5 год.
год. За умовою задачі, на весь шлях він витратив 5,5 год.
Складемо й розв'яжемо рівняння:
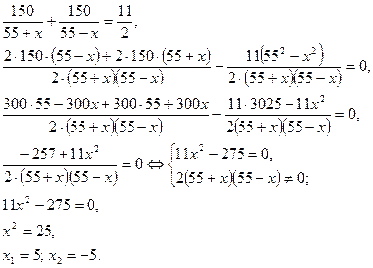
Розв'язок -5 не задовольняє умову задачі: швидкість — число додатне.
Відповідь: швидкість течії 5 км/год.
Задача 2 (на сумісну роботу ). Дві бригади, працюючи разом, виконали певне завдання за 4 дні. Скільки днів потрібно на виконання цієї роботи кожній бригаді окремо, якщо першій бригаді для цього потрібно на 6 днів менше, ніж другій?
Розв'язання.
Нехай перша бригада може виконати це завдання за х днів. Тоді другій потрібно (х + 6) днів. Це означає, що за один день перша бригада виконає 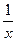 , а друга —
, а друга — 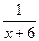 частину всього завдання. За умовою задачі, разом вони можуть виконати все завдання за 4 дні, тобто в день дві бригади, працюючи разом, виконують
частину всього завдання. За умовою задачі, разом вони можуть виконати все завдання за 4 дні, тобто в день дві бригади, працюючи разом, виконують 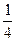 всього завдання.
всього завдання.
Складемо й розв'яжемо рівняння:
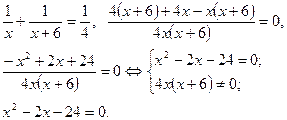
За теоремою Вієта: х1=6, х2=-4. Корінь х = -4 не задовольняє умову задачі, тому що час — число додатне.
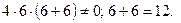
Відповідь: першій бригаді потрібно 6 днів, другій — 12 днів.


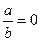 (де а і b — деякі цілі вирази) застосувати умову рівності дробу нулю;
(де а і b — деякі цілі вирази) застосувати умову рівності дробу нулю;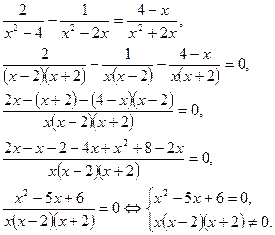
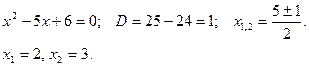
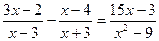 .
.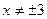
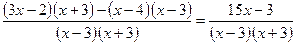
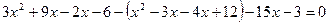
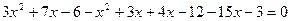 ,
, 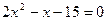
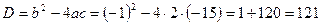
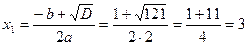 – сторонній корінь, тому що не задовольняє вимогам ОДЗ.
– сторонній корінь, тому що не задовольняє вимогам ОДЗ. 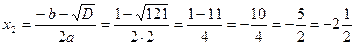
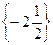 .
.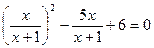 .
.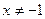 ,
, 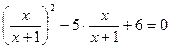 . Введемо заміну:
. Введемо заміну: 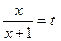 ,
, 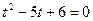 . За теоремою Вієта
. За теоремою Вієта 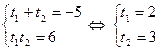
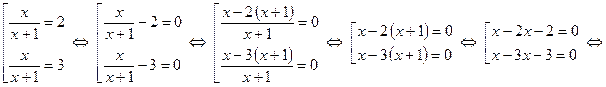
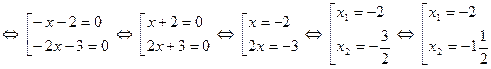
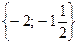 .
.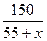
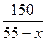
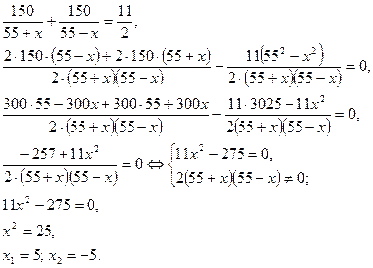
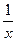 , а друга —
, а друга — 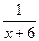 частину всього завдання. За умовою задачі, разом вони можуть виконати все завдання за 4 дні, тобто в день дві бригади, працюючи разом, виконують
частину всього завдання. За умовою задачі, разом вони можуть виконати все завдання за 4 дні, тобто в день дві бригади, працюючи разом, виконують 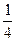 всього завдання.
всього завдання.