Побудова графіка функції двох змінних в MatLab на прямокутній області визначення змінних включає два попередні етапи:
1. Розбиття області визначення прямокутної сіткою.
2. Обчислення значень функції в точках перетину ліній сітки і запис їх в матрицю.
Побудуємо графік функції z(x,)= х2 + на 2 області визначення у вигляді квадрата х є [0, 1], y є [0, 1]. Необхідно розбити квадрат рівномірної сіткою (наприклад, з кроком 0.2) і обчислити значення функцій у вузлах, позначених точками.
Зручно використовувати два двовимірних масиву х та у розмірністю шість на шість для зберігання інформації про координати вузлів. Масив х складається з однакових рядків, в яких записані координати x1, х2, ..., х6, а масив містить однакові стовпчики з y1, 2, ..., 6. Значення функції у вузлах сітки запишемо у масив z такий же розмірності (6 6), причому для обчислення матриці Z використовуємо вираз для функції, але з поэлементными матричними операціями. Тоді, наприклад z(3,4) як раз буде дорівнює значенню функції z(x,y)у точці (х3, 4). Для створення масивів сітки х і за координатами вузлів в MatLab передбачена функція meshgrid, для побудови графіка у вигляді каркасної поверхні - функція mesh. Наступні оператори призводять до появи на екрані з графіком функції (крапка з комою в кінці операторів не ставиться для того, щоб проконтролювати генерацію масивів):
» [X, У] = meshgrid(0:0.2:1,0:0.2:1)
X =
0 0.2000 0.4000 0.6000 0.8000 1.0000
0 0.2000 0.4000 0.6000 0.8000 1.0000
0 0.2000 0.4000 0.6000 0.8000 1.0000
0 0.2000 0.4000 0.6000 0.8000 1.0000
0 0.2000 0.4000 0.6000 0.8000 1.0000
0 0.2000 0.4000 0.6000 0.8000 1.0000
y =
0 0 0 0 0 0
0.2000 0.2000 0.2000 0.2000 0.2000 0.2000
0.4000 0.4000 0.4000 0.4000 0.4000 0.4000
0.6000 0.6000 0.6000 0.6000 0.6000 0.6000
0.8000 0.8000 0.8000 0.8000 0.8000 0.8000
1.0000 1.0000 1.0000 1.0000 1.0000 1.0000
» Z = X.^2+Y.^2
Z =
0 0.0400 0.1600 0.3600 0.6400 1.0000
0.0400 0.0800 0.2000 0.4000 0.6800 1.0400
0.1600 0.2000 0.3200 0.5200 0.8000 1.1600
0.3600 0.4000 0.5200 0.7200 1.0000 1.3600
0.6400 0.6800 0.8000 1.0000 1.2800 1.6400
1.0000 1.0400 1.1600 1.3600 1.6400 2.0000
» mesh(X,Y,Z)
Які недоліки має побудований графік? І як їх усунути? Побудований графік і новий привести в електронному звіт по лабораторній роботі.
MatLab дозволяє наносити на графік додаткову інформацію, зокрема, відповідність кольорів значенням функції. Сітка генерується за допомогою команди meshgrid, що викликається з двома аргументами. Аргументами є вектори, елементи яких відповідають сітці на прямокутній області побудови функції. Можна використовувати один аргумент, якщо область побудови функції - квадрат. Для обчислення функції слід використовувати поелементні операції.
Розглянемо основні можливості, що надаються MatLab для візуалізації функцій двох змінних, на прикладі побудови графіка функції
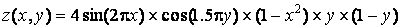
на прямокутній області визначення х є [-1,1], y є [0, 1].
Підготуємо матриці з координатами вузлів сітки і значеннями функції:
» [X, Y] = meshgrid(-1:0.05:1, 0:0.05:1);
» Z = 4*sin(2*пі*X).*cos(1.5*пі*Y).*(1-Х.^2).*Y.*(1-Y);
Для побудови каркасної поверхні використовується функція mesh, що викликається з трьома аргументами:
» mesh(X,Y,Z)
Колір ліній поверхні відповідає значенням функції. MatLab малює тільки видиму частину поверхні.
За допомогою команди hidden off можна зробити каркасну поверхню "прозорою", додавши приховану частина. Команда hidden on прибирає невидиму частину поверхні, повертаючи графіком колишній вигляд.
Функція surf будує каркасну поверхню графіка функції і заливає кожну клітину поверхні певним кольором, залежних від значень функції в точках, відповідних кутах клітини. У межах кожної клітини колір постійна. Подивіться результати виконання команди
» surf(X,Y,Z)
Команда shading flat дозволяє прибирати каркасні лінії. Для отримання поверхні, плавно залитої кольором, залежних від значень функції, призначена команда shading interp.
За допомогою shading faceted можна повернутися до поверхні з каркасними лініями.
3d графіки, одержувані з допомогою описаних вище команд, зручні для отримання уявлення про формі поверхні, проте за ним важко судити про значення функції. В MatLab визначена команда colorbar, яка виводить поруч з графіком стовпчик, що встановлює відповідність між кольором і значенням функції. Побудуйте за допомогою surf графік поверхні і доповніть його інформацією про кольорі.
» surf(X,Y,Z)
» colorbar
Команду colorbar можна застосовувати в поєднанні з усіма функціями, будують тривимірні об'єкти.
Користуючись кольоровий поверхнею, важко зробити висновок про значення функції в тій або іншій точці площині xy. Команди meshc або surfc дозволяють отримати більш точне уявлення про поведінку функції. Ці команди будують каркасну поверхню або залиту кольором каркасну поверхню і розміщують на площині xyлінії рівня функції (лінії постійності значень функції):
» surfc(X,Y,Z)
» colorbar
MatLab дозволяє побудувати поверхню, що складається з ліній рівня, за допомогою функції contour3. Цю функцію можна використовувати так само, як і описані вище mesh, surf, meshc і surfc з трьома аргументами. При цьому число ліній рівня вибирається автоматично. Є можливість задати четвертим аргументом у contour3 або число ліній рівня, або вектор, елементи якого рівні значень функції, які відображаються у вигляді ліній рівня. Завдання вектора (четвертого аргументу levels) зручно, коли потрібно досліджувати поведінку функції в деякій області її значень (зріз функції). Побудуйте, наприклад поверхню, що складається з ліній рівня, відповідних значень функції від 0 до 0.5 з кроком 0.01:
» levels = [0:0.01:0.5];
» contour3(X, Y, Z, levels)
» colorbar

