В операції над нечіткими множинами виділяють три основні логічні операції над нечіткими множинами: кон'юнкція, диз ’ юнкція і логічне заперечення. У середовищі Matlab існує можливість визначати кон ’ юктивні і диз ’ юнктивні оператори з точки зору минимаксной та імовірнісної інтерпретацій.
Розглянемо минимаксную інтерпретацію логічних операторів, в якій кон ’ юнктивний оператор представляє знаходження мінімуму - min (рис. П6, а), а дизъюнктивный - максимум - max (рис. П6, б).
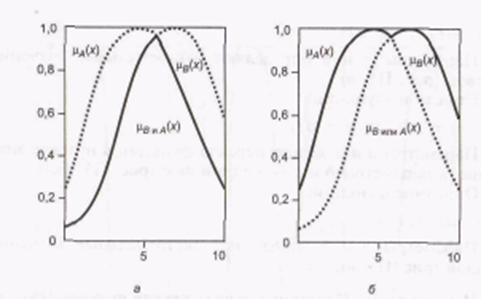
Рис. П6. Перетин () і об'єднання (в) нечітких множин
(мінімаксна інтерпретація)
Опис конъюнктивной функції: = min ([у1; у2]).
Опис дизъюнктивной функції: = тах ([у1; у2]).
Параметри у1 і у2 являють собою вихідні ФП. Функція min працює зі списком ФП. У Matlabсписок оформляється квадратними дужками, а елементи списку розділені крапкою з комою.
Приклад П7. Програма використання операцій min, max
x = 0 : 0,1 : 10;
subplot(1, 2, 1);
y1 = gaussmf (x, [3 5]);
у2 = gaussmf (x, [3 7]);
у3= min ([y1; y2]);
plot (x, [y1; у2],":"); побудова вихідних ФП пунктирною лінією
holdon;включення механізму додавання кривий в поточний графік
plot (x, у3);
holdoff; вимкнення приладу додавання кривий в поточний графік
subplot(1, 2, 2);
у4 = max([y1; у2]);
plot(x, [y1; у2], ":");
hold on;
plot (x, y4);
hold off.
Пунктирною лінією на графіках зображені вихідні ФП, а суцільною лінією - результат дії логічних операторів.
Мінімаксна інтерпретація є найбільш поширеною при побудові нечітких систем. Проте, на практиці досить часто використовується альтернативна імовірнісна інтерпретація конъюнктивных і дизъюнктивных операторів. Matlabмістить відповідні функції.
У рамках даної інтерпретації кон ’ юнктивний оператор являє собою оператор обчислення алгебраїчного твори - prod(мал. П7, ), а дизъюнктивный оператор - оператор обчислення алгебраїчної суми - рrоbоr(мал. П7, в).
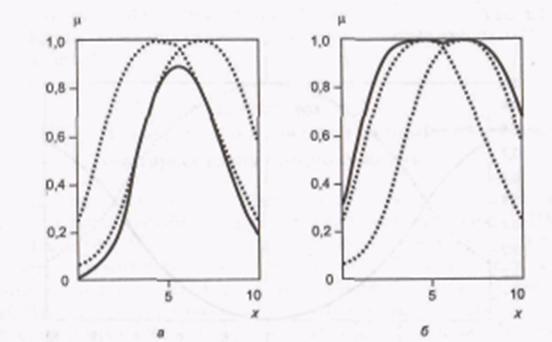
Рис. П7. Перетин () і об'єднання (б) нечітких множин
(імовірнісна інтерпретація)
Опис функції: = prod ([y1; у2])
Опис функції: = probor([y1; у2]).
Параметри y1і у2 являють собою вихідні ФП.
Приклад П8. Програма використання імовірнісних операторів кон'юнкції і диз ’ юнкції
х = 0 : 0,1 : 10;
subplot(1, 2, 1);
y1 = gaussmf (x, [3 5]);
y2 = gaussmf (x, [3,7]);
у3 = prod ([y1; y2]);
plot(x, [y1; у2],":");
hold on;
plot(x, y3);
hold off;
subplot(1, 2, 2);
y4 = probor ([y1; y2]);
plot (x, [y1; y2], ":");
hold on;
plot(x, y4);
holdoff.
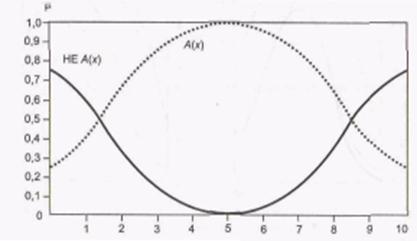
Рис. П8. Додаток нечіткої множини.
Додаток нечіткої множини є не що інше, як математичне подання вербального виразу «НЕ »(мал. П8), де - нечітка множина, що описує деякий розмите судження.
Опис функції доповнення: y = 1 - y*, де * - вихідна ФП.
Приклад П9. Програма використання операції доповнення
х = 0 : 0,1 : 10;
y1 = gaussmf(x, [3 5]);
= 1 - y1;
plot (х, y1, ":");
hold on;
plot(x, y);
hold off.




