Для відображення декількох графіків функцій однієї змінної на одних осях використовувалися можливості функцій plot, plotyy, semilogx, semilogy, loglog. Вони дозволяють виводити графіки декількох функцій, задаючи відповідні векторні аргументи парами, наприклад plot(x,f,x,g). Однак для об'єднання тривимірних графіків їх використовувати не можна. Для об'єднання таких графіків призначена команда hold on, яку потрібно поставити перед побудовою графіка. У наступному прикладі об'єднання двох графіків (площині і конуса) призводить до їх перетину. Конус задається параметрично наступними залежностями:
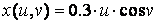 ,
, 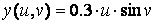 ,
, 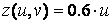 ,
, 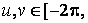
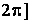 .
.
Для графічного відображення конуса спочатку необхідно згенерувати за допомогою двокрапки вектор-стовпчик і вектор-рядок, що містять значення параметрів на заданому інтервалі (важливо, що u - вектор-стовпчик, а v-вектор-рядок):
» u = [-2*pi:0.1*pi:2*pi]";
» v = [-2*pi:0.1*pi:2*pi];
Далі формуються матриці X, Y, що містять значення функцій 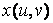 і
і 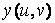 у точках, відповідних значень параметрів. Формування матриць виконується за допомогою зовнішнього твори векторів.
у точках, відповідних значень параметрів. Формування матриць виконується за допомогою зовнішнього твори векторів.
Примітка 2
Зовнішнім твором векторів 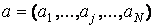 ,
, 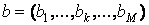 називається матриця
називається матриця 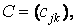
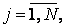
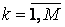 розміру N х M, елементи якої обчислюються за формулою
розміру N х M, елементи якої обчислюються за формулою 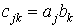 .
.
Вектор вектор-стовпцем ів MatLab представляється у вигляді двомiрного масива розміру N на один. Вектор-стовпчик при транспонировании переходить в вектор-рядок розміру один на М. Вектор-стовпчик і вектор-рядок є матриці, у яких один з розмірів дорівнює одиниці. Фактично, = abT, де множення відбувається за правилом матричного твори. Для обчислення матричного твори в MatLab використовується оператор "зірочка". Визначимо зовнішнє твір для двох векторів:
» a= [1;2;3];
» b= [5;6;7];
» C = a*b"
C =
5 6 7
10 12 14
15 18 21
Сформуємо матриці X,Y, необхідні для графічного відображення конуса:
» X = 0.3*u*cos(v);
» Y = 0.3*u*sin(v);
Матриця Z повинна бути того ж розміру, що і матриці X іY. Крім того, вона повинна містити значення, відповідні значень параметрів. Якщо б у функцію 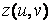 входило твір і і v, то матрицю Z можна було заповнити аналогічно матриць Xі Yза допомогою зовнішнього твори. З іншого боку, функцію z(u,v)можна представити у вигляді
входило твір і і v, то матрицю Z можна було заповнити аналогічно матриць Xі Yза допомогою зовнішнього твори. З іншого боку, функцію z(u,v)можна представити у вигляді 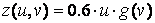 , де
, де 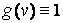 . Тому для обчислення Zможна застосувати зовнішнє добуток векторів
. Тому для обчислення Zможна застосувати зовнішнє добуток векторів 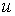 і
і 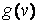 , де вектор-рядок
, де вектор-рядок 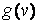 має ту ж розміри, що але складається з одиниць:
має ту ж розміри, що але складається з одиниць:
» Z = 0.6*u*ones(size(v));
Всі необхідні матриці для відображення конуса створені. Завдання площині виконується наступним чином:
» [X,Y] = meshgrid(-2:0.1:2);
» Z = 0.5*X+0.4*Y;
Тепер не складно записати і повну послідовність команд для побудови пересічних конуса і площині:
» u = [-2*pi:0.1*pi:2*pi]";
» v = [-2*pi:0.1*pi:2*pi];
» X = 0.3*u*cos(v);
» Y = 0.3*u*sin(v);
» Z = 0.6*u*ones(size(v));
» surf(X, Y, Z)
» [X,Y] = meshgrid(-2:0.1:2);
» Z = 0.5*X+0.4*Y;
» hold on
» mesh(X, Y, Z)
» hidden off
Команда hidden off застосована для того, щоб показати частина конуса, що знаходиться під площиною.
Зверніть увагу, що команда hold on поширюється на всі наступні висновки графіків в поточне вікно. Для розміщення графіків у нових вікнах слід виконати команду hold off. Команда hold on може застосовуватися і для розташування декількох графіків функцій однієї змінної, наприклад.
» plot(x,f,х,g)
Еквівалентно послідовності
» plot(х,f)
» hold on
» plot(x,g)

