Всі дані MatLab являє у вигляді масивів. Дуже важливо правильно зрозуміти, як використовувати масиви. Без цього неможливе ефективна робота в MatLab, зокрема побудова графіків, рішення завдань лінійної алгебри, обробки даних, статистики та багатьох інших. У даному підрозділі описані обчислення з векторами.
Масив - упорядкована, numbered сукупність однорідних даних. У масиву повинно бути ім'я. Масиви розрізняються за кількістю розмірностей або вимірювань: одномірні, двовимірні, багатовимірні. Доступ до елементів здійснюється за допомогою індексу. В MatLab нумерація елементів масивів починається з одиниці. Це означає, що індекси повинні бути більше або дорівнює одиниці.
Важливо зрозуміти, що вектор, вектор-рядок або матриця є математичними об'єктами, а одномірні, двовимірні або багатовимірні масиви - способи зберігання цих об'єктів в комп'ютері. Усюди далі будуть використовуватися слова вектор і матриця, якщо більший інтерес представляє сам об'єкт, ніж спосіб його зберігання. Вектор може бути записаний у стовпчик (вектор-стовпчик) і в рядок (вектор-рядок). Вектор-стовпці та вектор-рядки часто будуть називатися просто векторами, різниця буде зроблено в тих випадках, якщо важливий спосіб зберігання вектора в MatLab. Вектори та матриці позначаються курсивом, а відповідні їм масиви прямим моноширинним шрифтом, наприклад: "вектор міститься в масиві а", "запишіть матрицю R в масив r".
Введення додавання і віднімання векторів
Роботу з масивами почнемо з простого прикладу - обчислення суми векторів:
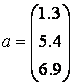 ,
, 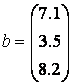 .
.
Для зберігання векторів використовуйте масиви а і b. Введіть масив а в командному рядку, використовуючи квадратні дужки й розділяючи елементи вектора крапкою з комою:
» a = [1.3; 5.4; 6.9]
a =
1.3000
5.4000
6.9000
Так як введене вираз не завершено крапкою з комою, то пакет MatLab автоматично вивів значення змінної а. Введіть тепер другий вектор, придушивши висновок на екран
» b = [7.1; 3.5; 8.2];
Для знаходження суми векторів використовується знак +. Розрахуйте суму, запишіть результат в масив і виведіть його елементи в командне вікно:
= a + b
с =
8.4000
8.9000
15.1000
Дізнайтеся розмірність і розмір масиву а за допомогою вбудованих функцій ndims і size:
» ndims(a)
ans =
2
» size(a)
ans =
3 1
Тож, вектор зберігається у двовимірному масиві а розміром три на один (вектор-стовпчик з трьох рядків і одного стовпця). Аналогічні операції можна зробити і для масивів b і c. Оскільки числа в пакеті MatLab представляються у вигляді двомiрного масива один на один, то при складанні векторів використовується той же знак плюс, що і для додавання чисел.
Введення вектор-рядки здійснюється в квадратних дужках, проте елементи слід розділяти пробілами або комами. Операції додавання, віднімання та обчислення елементарних функцій від вектор-рядків проводяться так само, як і з вектор-стовпцями, у результаті виходить вектор-рядок того ж розміру, що і вихідні. Наприклад:
» s1 = [3 4 9 2]
s1 =
9 2 3 4
» s2 = [5 3 3 2]
s1 =
5 3 3 2
» s3 = s1 + s2
s3 =
8 7 12 4
Примітка 1
Якщо розміри векторів, до яких застосовується додавання або віднімання, не збігаються, то видається повідомлення про помилку.
Природно, для знаходження різниці векторів слід застосовувати знак мінус, з множенням справа трохи складніше.
Введіть дві вектор-рядки:
» v1 = [2 -3 4 1];
» v2= [7 5 -6 9];
Операція .* (не вставляйте пробіл між точкою і зірочкою!) призводить до поэлементному множенню векторів однакової довжини. У результаті виходить вектор з елементами, рівними твором відповідних елементів вхідних векторів:
» u = v1.*v2
u =
14 -15 -24 9
За допомогою .^ здійснюється поелементне піднесення до степеня:
» р = v1.^2
p =
4 9 16 1
Показником мірою може бути вектор тієї ж довжини, що і підноситься до ступеня. При цьому кожен елемент першого вектора зводиться до степеня, рівну відповідного елементу другого вектора:
» p = vl.^v2
Р =
128.0000-243.0000 0.0002 1.0000
Поділ відповідних елементів векторів однакової довжини виконується з використанням операції ./
» d = v1/v2.
d =
0.2857-0.6000-0.6667 0.1111
Зворотне поелементне поділ (поділ елементів другого вектора на відповідні елементи першого) здійснюється за допомогою операції .\
» dinv = vl.\v2
dinv =
3.5000-1.6667-1.5000 9.0000
Отже, крапка в MatLab використовується не тільки для введення десяткових дробів, але і для зазначення того, що поділ або множення масивів однакового розміру має бути виконане поелементно.
До поелементним відносяться і операції з вектором і числом. Складання вектора і числа не призводить до повідомленням про помилку. MatLab додає число до кожного елементу вектора. Те ж саме справедливо і для віднімання:
» v = [4 6 8 10];
» s = v + 1.2
s =
5.2000 6.2000 9.2000 11.2000
» r = 1.2 - v
r =
-2.8000-4.8000-6.8000-8.8000
» r1 = v - 1.2
r1 = 2.8000 4.8000 6.8000 8.8000
Множити вектор на число можна як справа, так і зліва:
» v = [4 6 8 10];
» p = v*2
р. =
8 12 16 20
» pi = 2*v
pi =
8 12 16 20
Ділити за допомогою знака / можна вектор на число:
» р = v/2
p =
2 3 4 5
Спроба ділення числа на вектор призводить до повідомлення про помилку:
» р = 2/v
??? Error using ==> < / br />
Matrix dimensions must agree.
Якщо необхідно розділити число на кожен елемент вектора і записати результат в новий вектор, то слід використовувати операцію.
» w = [4 2 6];
» d = 12./w
d =
3 6 2
Всі вищеописані операції застосовні як до вектор-рядками, так і до вектор-стовпцях.
Особливість MatLab представляти всі дані у вигляді масивів є дуже зручною. Нехай, наприклад, потрібно обчислити значення функції sin відразу для всіх елементів вектора (який зберігається в масиві с) і записати результат в вектор d. Для отримання вектора d достатньо використовувати один оператор присвоювання:
» d = sin(с)
d =
0.8546
0.5010
0.5712
Отже, вбудовані в MatLab елементарні функції пристосовуються до увазі аргументів; якщо аргумент є масивом, то результат функції буде масивом того ж розміру, але з елементами, рівними значенням функції від відповідних елементів вихідного масиву. Переконайтеся в цьому ще на одному прикладі. Якщо необхідно знайти квадратний корінь з елементів вектора dзі знаком мінус, то достатньо записати:
» sqrt(-d)
ans =
0 + 0.9244i
0 + 0.7078i
0 + 0.7558i
Оператор присвоювання не використовувався, тому пакет MatLab записав відповідь у стандартну змінну ans.
Для визначення довжини вектор-стовпчиків або вектор-рядків служить вбудована функція length:
» length(s1)
ans =
4
З декількох вектор-стовпців можна скласти один, використовуючи квадратні дужки й розділяючи вихідні вектор-стовпці крапкою з комою:
» v1 = [1; 2];
» v2= [3; 4; 5];
» v = [v1; v2]
v =
1
2
3
4
5
Для зчеплення вектор-рядків також застосовуються квадратні дужки, але зчіплювані вектор-рядки відділяються пробілами або комами:
» v1 = [1 2];
» v2 = [3 4 5];
» v = [v1 v2]
v =
1 2 3 4 5
Робота з елементами векторів
Доступ до елементів вектор-стовпчика або вектор-рядки здійснюється за допомогою індексу, що укладається в дужки після імені масиву, в якому зберігається вектор. Якщо серед змінних середовища є масив v, визначений вектор-рядком
» v = [1.3 3.6 7.4 8.2 0.9];
то для виводу, наприклад його четвертого елемента, використовується індексація:
» v(4)
ans =
8.2000
Поява елемента масиву в лівій частині оператора присвоювання призводить до зміни в масиві
» v(2) = 555
v =
1.3000 555.0000 7.4000 8.2000 0.9000
З елементів масиву можна формувати нові масиви, наприклад
» u = [v(3); v(2); v(1)]
u =
7.4000
555.0000
1.3000
приміщення Для певних елементів вектора в інший вектор у заданому порядку служить індексація за допомогою вектора. Запис в масив w четвертого, другого і п'ятого елементів v здійснюється наступним чином:
» ind = [4 2 5];
» w = v(ind)
w =
8.2000 555.0000 0.9000
MatLab надає зручний спосіб звернення до блоків послідовно розташованих елементів вектор-стовпчика або вектор-рядка. Для цього служить індексація за допомогою знака двокрапки. Припустимо, що в масиві w, відповідному вектор-рядку з семи елементів, потрібно замінити нулями елементи з другого по шостий. Індексація при допомоги двокрапки дозволяє просто і наочно вирішити поставлену задачу:
» w = [0.1 2.9 3.3 5.1 2.6 7.1 9.8];
» w(2:6) = 0;
» w
w =
0.1000 0 0 0 0 0 9.8000
Присвоювання w(2:6) = 0 еквівалентно послідовності команд
w(2) = 0; w(3)=0; w(4)=0; w(5)=0; w(6)=0.
Індексація за допомогою двокрапки виявляється зручною при виділення частини з великого обсягу даних в новий масив:
» w - [0.1 2.9 3.3 5.1 2.6 7.1 9.8];
» wl = w(3:5)
wl =
3.3000 5.1000 2.6000
Складіть масив w2, що містить елементи w крім четвертого. У цьому випадку зручно використовувати двокрапку і зчеплення рядків:
» w2 = [w(l:3) w(5:7)]
w2 =
0.1000 2.9000 3.3000 2.6000 7.1000 9.8000
Елементи масиву можуть входити в вирази. Перебування, наприклад середнього геометричного з елементів масиву u, можна виконати наступним чином:
» gm = (u(l)*u(2)*u(3))^(l/3)
gm =
17.4779
Звичайно, цей спосіб не дуже зручний для довгих масивів. Для того щоб знайти середнє геометричне, необхідно набрати у формулі всі елементи масиву. В MatLab існує досить багато спеціальних функцій, що полегшують подібні обчислення.
Застосування функцій обробки даних до векторах
Перемножування елементів вектора-стовпчика або вектора-рядки здійснюється за допомогою функції prod:
» z= [3; 2; 1; 4; 6; 5];
р = prod(z)
p = 720
Функція sum призначена для підсумовування елементів вектора. З її допомогою нескладно обчислити середнє арифметичне елементів вектора z:
» sum(z)/length(z)
ans =
3.5000
В MatLab є спеціальна функція mean для обчислення середнього арифметичного:
» mean(z)
ans =
3.5000
Для визначення мінімального і максимального з елементів вектора служать вбудовані функції min, max:
» m1 = max(z)
m1 =
6
» m2 = min(z)
m2 =
1
Часто необхідно знати не тільки значення мінімальної чи максимальної елемента в масиві, але і його індекс (порядковий номер). У цьому випадку вбудовані функції min, max необхідно використовувати з двома вихідними аргументами, наприклад
» [m, k] = min(z)
m =
1
k =
3
У результаті змінної m буде присвоєно значення мінімального елемента масиву z, а номер мінімального елемента занесений в змінну k.
Для отримання інформації про різні способи використання функцій слід набрати в командному рядку help та ім'я функції. MatLab виведе у командне вікно всілякі способи звернення до функції з додатковими поясненнями.
У число основних функцій для роботи з векторами входить функція впорядкування вектора за зростанням його елементів sort.
» r = [9.4-2.3-5.2 7.1 0.8 1.3];
» R = sort(r)
R =
-5.2000-2.3000 0.8000 1.3000 7.1000 9.4000
Можна впорядкувати вектор за спаданням, використовуючи цю ж функцію sort:
» R1 = -sort(-r)
R1 =
9.4000 7.1000 1.3000 0.8000 -2.3000-5.2000
Упорядкування елементів у порядку зростання їх модулів здійснюється із залученням функції abs:
» R2 = sort(abs(r))
R2 =
0.8000 1.3000 2.3000 5.2000 7.1000 9.4000
Виклик sort з двома вихідними аргументами призводить до утворення масиву індексів відповідності елементів впорядкованого і вихідного масивів:
» [rs, ind] = sort(r)
rs =
-5.2000-2.3000 0.8000 1.3000 7.1000 9.4000
ind =
3 2 5 6 4 1


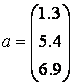 ,
, 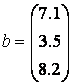 .
.