Типів проектів багато, рекомендується використовувати проект зі своєю віконної функцією, в цьому випадку максимальну швидкодію.
Універсальні
1.Изображения пікселя і отримання його кольори.
СOLORRF SetPixel (HDC hDC,
int x, y, //координати
COLORREF color); //колір
Всі фігури малює PEN, за замовчуванням товщина лінії 1 піксель.
BOOL LineTo(HDC hDC, int x, int y);
Лінія ведеться від точки з координатами (х,у) до поточної точці контексту (0,0).
Возвращает: 0 - False, якщо не може малювати лінію
1 - True
Установка поточної точки контексту.
BOOL MoveToEx (HDC hDC, int x, int y, LPPoint lpOldxy);
Визначення поточної точки.
BOOL GetCurrenPosition(HDC hDC, LPPOINT pxycurrent);
Зображення кривих
Зображення прямокутників
BOOL Rectangle (HDC hDC, int x1, int y1, int x2, int y2);
Прямокутник округленими кутами.
BOOL RoundRectangle (HDC hDC, int x1, int y1, int x2, int y2, int Dx, int Dy);
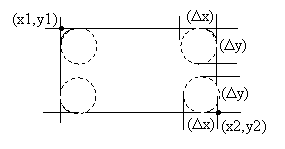
Еліпс.
BOOL Ellipse(HDC hDC, int x1, int y1, int x2, int y2);

Зображення дуги еліпса.
BOOL Arc (HDC hDC, int x1, int y1, int x2, int y2, int x3, int y3, int x4, int y4);
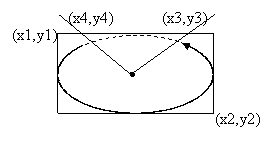
Замкнута дуга
Chord (hDC, int x1, int y1, int x2, int y2, int x3, int y3, int x4, int y4);

Еліптичний сектор
Pie (hDC, int x1, int y1, int x2, int y2, int x3, int y3, int x4, int y4);

Фігури з'єднання великого числа точок.
Кусково-лінійна апроксимація
Будь-яка крива - послідовність прямих.
POINT mT[100];
mT[0].x = 1;
mT[0].y = 1;
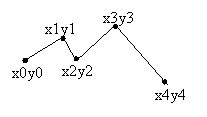
BOOL Polyline (HDC hDC, POINT mt, int N)
; // N - число тічок, які потрібно з'єднати
PolylineTo(hDC,mT,Nz); //Малювання не точки з координатами(х0,y0), а з поточної точки поля.
З'єднання точок з замиканням і заливкою.
Bool Polygon(HDC hDC, POINT mT, int N);

Малювання декількох кривих
DWORD mNT[k];
mNT= {3,4,2};
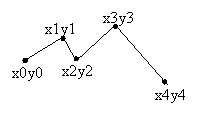
BOOL PolyPolyline (HDC hDC, POINT mt, Dword mNT ,Dword k)- Dword k кількість кривих;

Створення декількох замкнутих.
Bool Polygon(HDC hDC, POINT mt, Dword mNT ,Dword k)
Якщо лінії перетинаються.
SetPolyFillMode(hDC, int ARTERNATE) - заливається повністю.
Або SetPolyFillMode(hDC, int ЗАВОДЯЧИХ) - то так

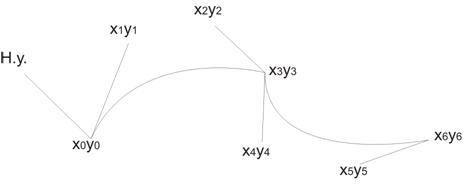
Крива бизье - апрокссимация параболами другого порядку, можна зробити плавний перехід.
Технологія зображення цих кривих лежить в основі побудови шейдерів в CorelDraw.
Основна ідея: ми говоримо де рассположена точка і крутість майбутньої параболи (tg) і ставимо її прямою лінією.
PolyBezier(HDC LDC, const Point mB, DWORD N);
PolyBezierTo(HDC LDC, const Point mB, DWORD N);
!!! Якщо лінії кривий Bezier перетинаються, то заливка автоматично не виконується.
Додаткові можливості малювання прямокутників не пременяя BRUSH і PEN:
RECT r, *pr
{ r.left; //x1
r.top; //y1
r.right; //x2
r.bottom; //y2
}
Можна створювати довільні кольору не змінюючи контексту.
Для зображення використовується своя BRUSH
 HBRUSH hBrush = Create SclidBrush (RGB(R,G,B));
HBRUSH hBrush = Create SclidBrush (RGB(R,G,B));
від 0-255 для кожного,
тобто 16 млн. кольорів
Заливка області без контуру.
int FillRect(HDC hDC, LPRECT &r, HBRUSH hBrush)
Інверсія кольору усередині заданого прямокутника
IuVertRect (HDC hDC, LPRECT &r);
Зображення прямокутника з контуром заданого кольору по імені кольору в Pent в контексте :
FrameRect(HDC hDC, LPRECT &r, HBRUSH hBrush);
Особливості:
Зсув прямокутників.
OffSetRect(&r, Dx, Dy);
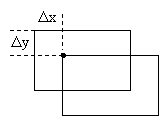
Зміна полів у Rect шляхом зміни його значень у структурі
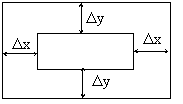
IntLateRect(&r, Dx, Dy);
Потрібно знайти координати прямокутника, який їх повністю охоплює
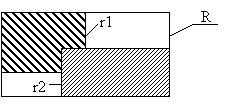

Unicn Rect (&R, &r1, &r2);
Знаходження прямокутника
InterSectRect(&R, &r1, &r2);
















