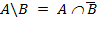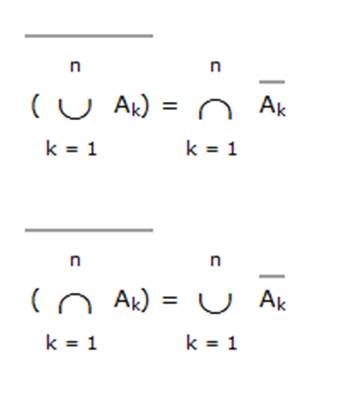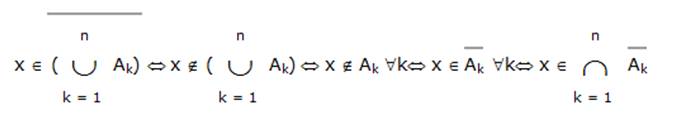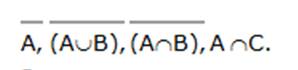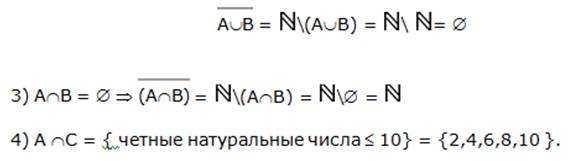У цьому пункті ми опишемо деякі способи отримання нових множин з вже наявних. Ці способи зазвичай називаються операціями над множинами. Основні властивості цих операцій і зв'язку між ними прийнято називати алгеброю множин.
Визначення. Об'єднанням (сумою двох множин A і B називається безліч (його прийнято позначати 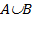 ) що складається з тих, і лише тих елементів, які належать хоч одному з цих множин - або A або B.
) що складається з тих, і лише тих елементів, які належать хоч одному з цих множин - або A або B.
мовою кванторов ми будемо записувати цю операцію наступним чином:
Приклад. Розглянемо множини A= {1, 2, 3, 4}, B = {1,3,5}, C = {5,6}. Тоді, відповідно введеному визначення отримуємо:
Аналогічно визначається об'єднання (сума) 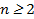 множин A1,A2, ..., An. Поєднанням цих множин називається безліч, що позначається
множин A1,A2, ..., An. Поєднанням цих множин називається безліч, що позначається 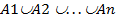 , що складається з тих, і лише тих елементів, які належать хоч одному з цих множин.
, що складається з тих, і лише тих елементів, які належать хоч одному з цих множин.
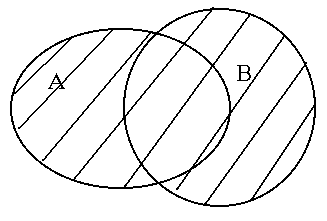
Досить часто для візуального зображення цих операцій над множинами використовують так звані, кола Ейлера (діаграми Венна). Безлічі при такому підході зображують колами, а результат операції зафарбовують або заштриховывают. Ось так виглядає результат операції об'єднання двох множин.
Визначення. Перетином (твором) двох множин A і B називається безліч (його прийнято позначати 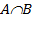 ) що складається з тих, і лише тих елементів, які належать кожному з множин A і B.
) що складається з тих, і лише тих елементів, які належать кожному з множин A і B.
мовою кванторов ми будемо записувати цю операцію таким чином:
Приклад. В рамках введених в попередньому прикладі визначень множин A, B, C ми отримуємо:
Також як ми робили раніше, можна визначити перетинання (твір) кінцевого числа множин.
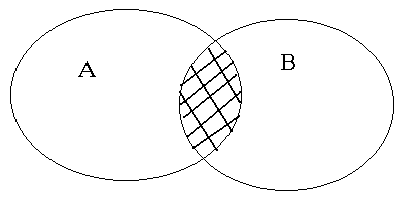
На колах Ейлера перетинання множин виглядає наступним чином:
Буває зручно ввести поняття "універсального" безлічі U, яке за припущенням містить всі використовувані нами безлічі.
Введені операції над множинами володіють властивостями комутативності:
і властивістю асоціативності:
справедливість цих властивостей слід із самих визначень операцій перетину і об'єднання множин, тому, звичайно, дужки в таких групових операціях опускають.
Має місце також закон взаємної дистрибутивности:
Перейдемо до нової операції над множинами. Ця операція визначається тільки для двох множин.
Визначення. Різницею двох множин A і B називається безліч (його зазвичай позначають A\B або A-B), що складається з тих, і лише тих елементів, які належать безлічі A і не належать безлічі B.
На колах Ейлера
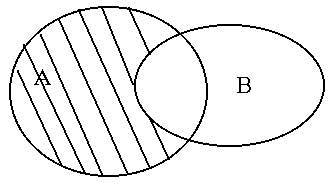
Приклад. В рамках введених в попередньому прикладі визначень множин A, B, C справедливі наступні результати
A\B = {2,4}; B\C = {1,3}; A\C = A. |
|
Майже очевидно наступне властивість, яку також можна прийняти за визначення різниці двох множин:
Визначення. Симетричною різницею множин A і B називається безліч називається через A  B і визначається наступним чином:
B і визначається наступним чином:
На колах Ейлера ця операція виглядає ось як
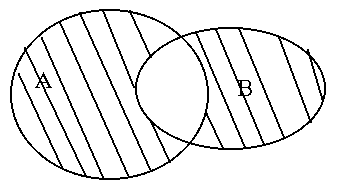
Приклад.
a) 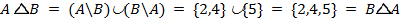 ; ; |
|
b) 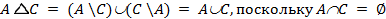 . . |
|
Крім того, справедливо наступне властивість:
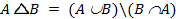 . . |
|
Доказ цього властивості, як і інших тверджень про рівність будь-яких множин, полягає в тому, щоб припустивши приналежність певного елемента x безлічі з лівої частини рівності довести, що цей самий елемент належить множині, що стоїть в правій частині рівності і навпаки.
Перейдемо до доказу. Нехай 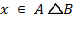 , що за визначенням симетричною різниці означає, що
, що за визначенням симетричною різниці означає, що 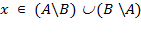 . Тут можливі два варіанти: або
. Тут можливі два варіанти: або 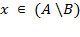 або
або 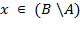 . У першому випадку ми отримуємо:
. У першому випадку ми отримуємо: 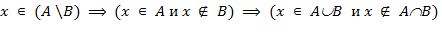 звідки очевидно випливає, що
звідки очевидно випливає, що 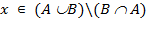 . Ситуація, коли
. Ситуація, коли 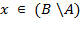 розглядається аналогічно.
розглядається аналогічно.
Отже, ми довели, що якщо певний елемент x належить безлічі з лівої частини рівності, то з цього випливає, що він належить множині, що стоїть в правій частині рівності. Тепер нам необхідно довести зворотне включення.
Нехай 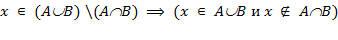 . Тут можливі 2 ситуації: або
. Тут можливі 2 ситуації: або 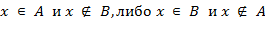 . Давайте розглянемо перший випадок: нехай
. Давайте розглянемо перший випадок: нехай 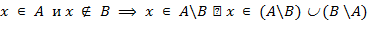 . Другий випадок доводиться аналогічно.
. Другий випадок доводиться аналогічно.
Отже, ми повністю довели заявлене властивість. При доведенні подібних тверджень величезну роль відіграє те властивість, що якщо певний елемент x належить деякого безлічі X, то він, очевидно, буде належати і об'єднання множини X з довільним іншим безліччю.
Досить часто виявляється зручним ввести поняття "універсального" безлічі U, яке містить всі розглянуті нами безлічі.
Визначення. Безліч U\A називається доповненням множини A (до універсальної множини) і позначається через ` .
.
Принцип подвійності. Нехай Ak, k = 1,...,n - деякі підмножини універсальної множини U, тоді мають місце наступні рівності:
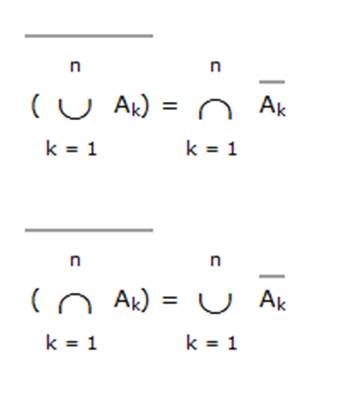
Ці рівності зв'язуючі операції перетину і об'єднання множин і їх доповнень до універсальної множини зазвичай називають співвідношенням принципу подвійності.
Доведемо перше співвідношення:
Зауважимо, що в наведеному доказі всі твердження про елемент x з'єднані знаками 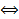 , що дозволяє одночасно будувати доказ затвердження в обидві сторони.
, що дозволяє одночасно будувати доказ затвердження в обидві сторони.
Справедливість другого співвідношення доводиться аналогічно.
Приклад. Визначимо наступні безлічі: A - безліч парних натуральних чисел; B - безліч непарних натуральних чисел; C - безліч натуральних чисел, не більше 10. Як "універсального" безлічі ми будемо розглядати багато натуральних чисел  . Наша задача полягає в тому, щоб описати наступні безлічі:
. Наша задача полягає в тому, щоб описати наступні безлічі:
- це безліч непарних натуральних чисел, тобто безліч B
2) Кожна натуральне число є або парних або непарних, тому 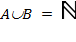 . Отже,
. Отже,
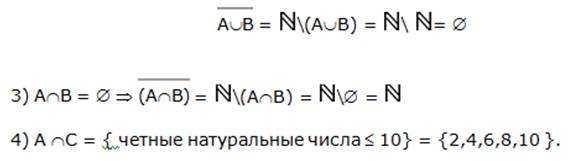
Якщо тепер вважати, що в нашому розпорядженні є універсальне безліч U, то операції 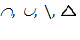 можна визначати один через одного і фактично ввести деякий базис операцій у алгебри множин.
можна визначати один через одного і фактично ввести деякий базис операцій у алгебри множин.
Приклади.
1) 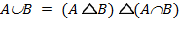
2) 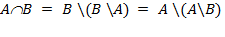
3)