Більшу частину понять дискретної математики можна визначити за допомогою поняття множини. Безліч - основне, первинне і неопределяемое поняття математики. Безліччю прийнято називати набір, сукупність деяких об'єктів, при цьому природа самих об'єктів, що становлять те чи інше безліч нас і не буде цікавити. Творець теорії множин Георг Кантор давав таке визначення множини - "безліч є багато, conceivable нами як ціле."
Об'єкти, з яких складається те чи інше безліч прийнято називати елементами цієї множини. У математики вживаються такі синоніми терміну безліч - система, клас, сукупність. Як вже говорилося, безлічі можуть бути самої різної природи, наприклад, безліч всіх дерев в нашому рідному місті на 29 липня 1974 року, в якості іншого прикладу безлічі можна прийняти таке визначення безліч всіх студентів, які сидять зараз в сусідній аудиторії. У першому прикладі елементами безлічі є дерева, а в другому студенти.
У математики розглядаються більш специфічні безлічі, що складаються з чисел, кривих, множин і т.д. Безлічі прийнято позначати великими літерами латинського алфавіту, а елементи цих множин - маленькими літерами латинського алфавіту. Наприклад, множини A, B, ... X, Y, Z і відповідно елементи a, b,... x, y, z.
Наведемо стандартні позначення для найбільш часто використовуваних числових множин:
- безліч натуральних чисел, 
= {1,2,3,... };
- безліч цілих чисел, 
= 
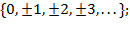
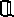- безліч раціональних чисел,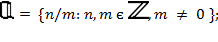 
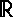- безліч дійсних (речових) чисел.
математики прийнято використовувати такі позначки:
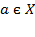- "елемент a належить множини X";
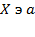- "безліч X містить елемент a", щовзагалі кажучи, теж саме;
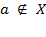- "елемент a не належить множини X";
- квантор довільності: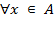 
- "для будь-якого елемента x множини A";
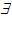- квантор існування: 
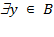- "існує (знайдеться) елемент y з безлічі B";
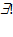- квантор існування і єдиності: 
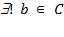- "існує єдиний елемент b з безлічі C";
: - "такий, що; володіє властивістю", зазвичай таким значком доповнюється попередній квантор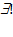 
--> - квантор проходження - "якщо ..., то ...";
<--> - квантор рівносильності - "тоді і тільки тоді";
Безліч може містити багато елементів, а може лише кілька, наприклад, безліч російських букв містить рівно 33 елемента. Безліч натуральних чисел 
містить нескінченно багато елементів. Може бути і граничний випадок, коли безліч взагалі не містить елементів, наприклад, безліч дійсних корінь рівняння x4+8 = 0.
Визначення. Безліч не містить жодного елементу називається порожнім безліччю і позначається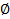 
.
В загальному випадку безлічі бувають кінцеві і нескінченні.
Визначення. Кінцеве безліч це таке безліч, для якого існує натуральне число, що дорівнює числу його елементів.
Наприклад, безліч російських букв - кінцеве безліч, оскільки існує натуральне число 33, яка дорівнює кількості елементів цієї множини.
Визначення. Безліч, не є кінцевим називається нескінченним безліччю.
Вже розглянута нами безліч натуральних чисел 
- безліч, оскільки немає такого натурального числа, що дорівнювало б його елементів.
Якщо безліч A - кінцеве безліч, то через |A | прийнято позначати число його елементів і називати |A | потужністю безлічі A. Поняття потужності вводиться і для нескінченних множин, однак ми будемо розглядати його трохи пізніше.
Приклад. Нехай безліч складається з наступних елементів { січень, лютий, березень, квітень, травень, червень, липень, серпень, вересень, жовтень, листопад, грудень } - це безліч місяців одного року. Зрозуміло, що потужність <|A| em>заданого таким чином множини A дорівнює 12. Це число елементів множини A або, що те ж саме кількість місяців одного року.
Визначення. Два кінцевих множини A і B називаються рівними, якщо вони складаються з одних і тих же елементів. Якщо множини A і B рівні, то ми будемо писати A = B, інакше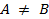 
Таким чином, ми отримали наступне визначення:
Визначення. Два кінцевих множини A і B не рівні між собою, якщо в безлічі A є елемент не належить безлічі B або навпаки.
Згідно такого визначення рівності множин ми природно отримуємо, що всі порожні безлічі рівні між собою або що те ж саме, що існує тільки одне порожнє безліч.
Приклади. a) Безлічі{ 0, 1, 2} = { 1, 2, 0} рівні між собою і тому між ними ми можемо поставити знак рівності - вони кінцеві і складаються з одних і тих же елементів.
b) Розглянемо тепер три множини A = { 0, 1 }, B= {{ 0, 1 },2} і C= {{{ 0, 1 }, 2} 3}. Між цими множинами справедливі наступні співвідношення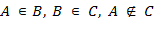 
.
Існує два основних способи завдання множин: перерахування та опис. Безліч можна задати перерахувавши всі його елементи, а також за допомогою оголошення властивості, що визначає які елементи належать, а які не належать описуваного безлічі.
Давайте згадаємо приклад з місяцями. Ми ставили це безліч переліком всіх його елементів: січень, лютий, .... Перерахуванням можна поставити тільки кінцеві безлічі. Важко перелічити всі натуральні числа від 2 до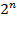 
. Опис цієї множини в попередньому реченні виділено курсивом шрифтом. Нескінченні безлічі можна поставити тільки описом властивості його елементів. Поверніться трохи назад і подивіться, як ми визначали безліч раціональних чисел 
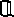фактично це було опис властивостей його елементів. Безліч 
