Система числення - (number system) - це сукупність прийомів і правил найменування та позначення чисел.
Цифра - безліч символів, застосовуваних у даній системі числення.
Основними типами даних, які зустрічаються при обробці інформації в ЕОМ, є числа, які представлені в двійковій системі числення, а також епізоду-цифрові символи. Для кодування символів використовуються спеціальні коди, найбільш поширеними з яких є семи - і восьми бітні двійкові коди, наприклад, ASCІІ коди (американський стандартний код для передачі інформації).
Тип системи числення визначається за її підстави. Системи можна класифікувати:
- непозиционные - системи, в яких символ (буква, цифра, ієрогліф) зберігає своє значення незалежно від його положення в числі;
- позиційні - системи, в яких значення символу залежить від його положення (позиції) в числі.
Прикладом непозиционной системи числення є римська система. В римській системі числення використовують такі цифри:
І = 1,
V = 5,
Х = 10,
L = 50,
= 100,
D = 500,
M = 1000.
У цій системі число 2005 записують як ММV, а 1982 як MCMLXXXII.
Будь-яке число Ni у позиційній системі числення з основою g можна представити у вигляді:
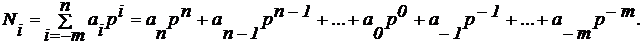
де ai -кількість одиниць цього розряду;
p - основа системи (будь-яке ціле від 2 до 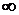 );
);
i - номер розряду.
Якщо відомо підставу, то число можна записати як
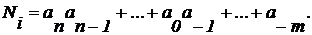
пВ обчислювальної техніки найбільш часто використовуються позиційні системи числення: десяткова, двійкова і шістнадцяткова.
Десяткова система числення. В десятковій системі числення:
р = 10;
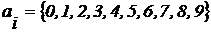
Наприклад, в десятковій системі числення число 237,58 представлено як
2?102 + 3?101 + 7?100 + 5?10-1 + 8?10-2.
Символ "," називається комою (точкою) системи числення. Частина числа, яка розміщена ліворуч від цього символу носить назву цілої частиною числа, праворуч - дробової частини.
Двійкова система числення. Для двійкової системи числення:
р = 2;
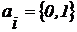
Наприклад, в двійковій системі числення число 101 представлено як
1012 =1?22 + 0?21 + 1?20 = 510 .
Гідність двійкової системи числення:
- Найменше число цифр для запису чисел.
- Простота виконання арифметичних операцій. Використовується тільки одна арифметична операція додавання і зсув.
- Простота технічної реалізації пристроїв для обробки й зберігання двозначних чисел (всього 2 стану «0» і «1»).
- Надійність технічних пристроїв.
Недоліки двійкової системи числення:
- Громіздкість чисел;
- Велика розрядність пристроїв для обробки й зберігання двозначних чисел.
Шістнадцяткова система числення. Для шістнадцятковій системі числення:
р = 16;
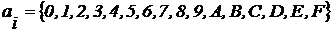 .
.
В системах числення з основою більше 10 використовують десять цифр для молодших значень цифр розрядів і латинські літери А, В, С...- для старших.
пНапример, в шістнадцятковій системі числення число 10A представлено як 10A16=1?162 + 0?161 + 10?160 =256+0+10=26610.
Шістнадцяткова система числення використовується для більш короткою і зручною запису двійкових кодів команд, операндів і адрес.
Якщо необхідно позначити основа системи числення, то використовують числові індекси або латинські літери: для двійкових чисел індекс 2 або літера В (Віпагу), для десяткового - індекс 10 або літера D (Decіmal), для шістнадцятирічного - індекс 16 або літера Н (Hexadecіmal).

