Розв'язування квадратного рівняння способом виділення квадратного двочлена розглянемо на прикладі.
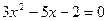 .
.
Розв'язання
Поділимо всі коефіцієнти рівняння на перший коефіцієнт: 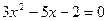 |:3 й отримаємо таким чином зведене квадратне рівняння:
|:3 й отримаємо таким чином зведене квадратне рівняння:
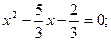
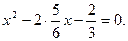 Для того щоб отримати повний квадрат,
Для того щоб отримати повний квадрат,
треба додати і відняти від лівої частини рівняння 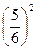 :
:
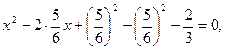
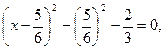
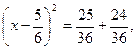
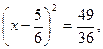
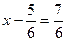 або
або 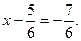
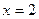 або
або 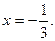
Відповідь: 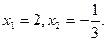
Формула коренів квадратного рівняння
Корені квадратного рівняння ax2+bx+c = 0(a 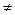 0)
0)
знаходять за формулою 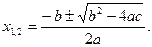 Вираз b2 – 4ac називається дискримінантом і позначається буквою D.
Вираз b2 – 4ac називається дискримінантом і позначається буквою D.
Кількість коренів
1. Якщо D<0, рівняння не має коренів.
2. Якщо D = 0, рівняння має один корінь: 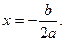
3. Якщо D>0, рівняння має два корені: 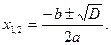
Для квадратних рівнянь із парним другим коефіцієнтом зручніше користуватися формулою, наведеною нижче.
Позначимо 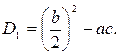 Тоді для
Тоді для 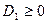 маємо
маємо 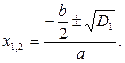
Теорема Вієта
Теорема 1 (Вієта). Якщо незведене квадратне рівняння ах2 +bx+c = 0 має два корені, то 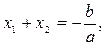
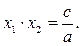
Якщо зведене квадратне . рівняння х2 + рх+q = 0 має два корені, то
х1+ х2=- р; xlx2 = q.
Коли рівняння має один корінь, його можна вважати за два рівних: х1=х2. Тоді для незведеного квадратного рівняння 2х1= 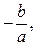
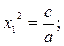 для зведеного 2х1= - p,
для зведеного 2х1= - p,
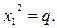
Для того щоб скористатися формулами теореми Вієта, треба спочатку переконатися у наявності коренів рівняння, перевіривши знак його дискримінанта.
Приклади
Знайти суму й додаток коренів рівняння,
1) Зх2-5х+2 = 0;
D = 25-3.2.4 = 1 — додатне число, і це означає, що рівняння має два корені.
Отже, х1+х2=5/3; , х1 х2=2/3.
2) х2+Зх+10=0;
D = 9 - 40 = -31 — від'ємне число.
Рівняння не має коренів, знайти їх суму та добуток неможливо.
Теорема 2 (обернена до теореми Вієта зведених квадратних рівнянь). Якщо сума й добуток чисел х1 і х2 дорівнюють відповідно р і q, то х1 і х2 є коренями рівняння х2+pх+q=0.
Із теореми Вієта випливає, що цілі розв'язки рівняння х2+pх+q=0 є дільниками числа q. Користуючись оберненою теоремою, можна перевірити, чи є та чи інша пара дільників q коренями даного рівняння. Це дає можливість усно розв'язувати значну кількість зведених квадратних рівнянь.
Під час розв'язування треба також враховувати такі висновки з теореми Вієта
1. Якщо q <0, х1 і х2 мають різні знаки.
2. Якщо q >0, х1 і х2 обидва від'ємні чи обидва додатні. Знак суми х1 і х2 є протилежним до знака р.
Приклад. х2 - 8х - 0=0. За теоремою Вієта:
х1 х2 =-9; х1+ х2 =8; 9 = 1.9 = 3.3. Очевидно, що 8 = 9+(-1).
Відповідь: х1 = -1; х2 = 9.
1) Розв’язати квадратне рівняння 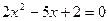 .
.
Розв’язання. 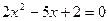
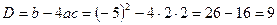
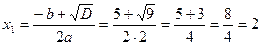
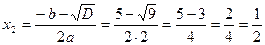 .
.
Відповідь. 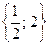 .
.
2) Розв’язати квадратне рівняння 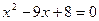 .
.
Розв’язання. 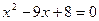
За теоремою Вієта: 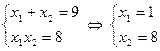 .
.
Відповідь. 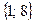 .
.


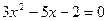 .
.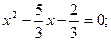
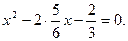 Для того щоб отримати повний квадрат,
Для того щоб отримати повний квадрат,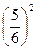 :
: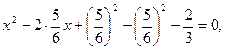
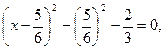
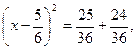
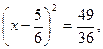
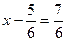 або
або 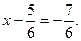
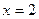 або
або 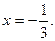
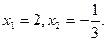
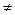 0)
0)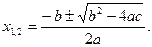 Вираз b2 – 4ac називається дискримінантом і позначається буквою D.
Вираз b2 – 4ac називається дискримінантом і позначається буквою D.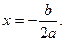
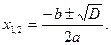
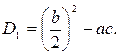 Тоді для
Тоді для 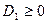 маємо
маємо 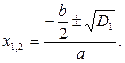
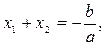
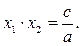
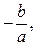
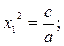 для зведеного 2х1= - p,
для зведеного 2х1= - p,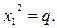
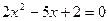 .
.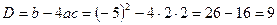
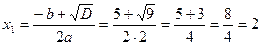
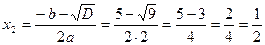 .
.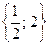 .
.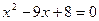 .
.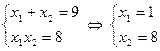 .
. .
.