Дослідимо спектр сигналу, що виникає на виході ідеального імпульсного модулятора та задано виразом (1.309). Підмітимо, що сигнал виду МІП з точністю до коефіцієнта пропорційності 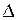 дорівнює добутку функції
дорівнює добутку функції 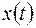 та дискретизуючої послідовності
та дискретизуючої послідовності  :
:
 . .
| (1.310)
|
Згідно з даною моделлю, значення сигналу в паузах умовно вважаються рівним нулю.
Відомо, що спектр добутку двох сигналів пропорційний згортці їх спектральних щільностей (див. п. 1.2). Тому якщо відомі закони відповідності сигналів та спектрів:
 , ,
|
|
то спектральна щільність МІП-сигналу
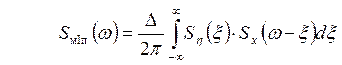 . .
| (1.311)
|
Щоб знайти спектральну щільність 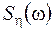 дискретизуючої послідовності, розкладемо періодичну функцію
дискретизуючої послідовності, розкладемо періодичну функцію  в комплексний ряд Фур'є:
в комплексний ряд Фур'є:
 . .
|
|
Коефіцієнти цього ряду 
 . .
|
|
Тут тривалість прямокутних імпульсів, які формують вибірки, прямує до нуля.
Звернувшись до формули (1.130) 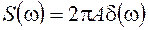 , отримаємо
, отримаємо
 . .
| (1.312)
|
інакше спектр дискретизуючої послідовності складається з нескінченної сукупності дельта-імпульсів у частотній області. Дана спектральна щільність є періодичною функцією з періодом 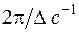 .
.
Нарешті, підставивши формулу (1.312) в (1.311) і змінивши порядок проходження операцій інтегрування та додавання, знаходимо
 . .
| (1.313)
|
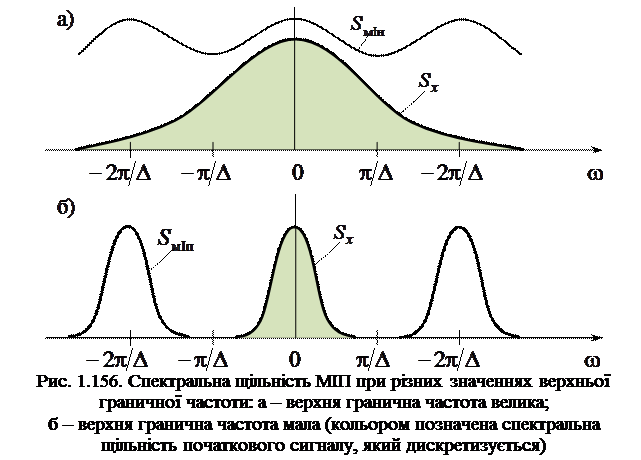
Отже, спектр сигналу, отриманого в результаті ідеальної дискретизації нескінченно короткими стробуючими імпульсами, є сума нескінченного числа «копій» спектра вихідного аналогового сигналу. Копії розташовуються на осі частот через однакові інтервали  , які рівні значенню кутової частоти першої гармоніки дискретизуючої імпульсної послідовності (рис. 1.156,а, б)
, які рівні значенню кутової частоти першої гармоніки дискретизуючої імпульсної послідовності (рис. 1.156,а, б)


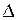 дорівнює добутку функції
дорівнює добутку функції 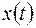 та дискретизуючої послідовності
та дискретизуючої послідовності  :
: .
.
 ,
,
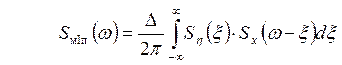 .
.
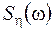 дискретизуючої послідовності, розкладемо періодичну функцію
дискретизуючої послідовності, розкладемо періодичну функцію  .
.

 .
.
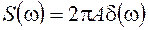 , отримаємо
, отримаємо .
.
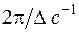 .
. .
.

 , які рівні значенню кутової частоти першої гармоніки дискретизуючої імпульсної послідовності (рис. 1.156,а, б)
, які рівні значенню кутової частоти першої гармоніки дискретизуючої імпульсної послідовності (рис. 1.156,а, б)