1.2.1 Основні принципи побудови блокових
симетричних шифрів
Ще в роботі Шенона «Таємність і терміновість» були сформульовані такі основні принципи перетворення повідомлень, що можуть забезпечити високу стійкість блокового шифрування (мал.3.5):
1. Переплутування (нелінійне перетворення підстановка) символів.
2. Перемішування (розосередження, перестановка) символів.
3. Ітерування (повторення пунктів 1 і 2 багаторазово).
Достатньо складно задати загальне нелінійне перетворення для блоків великої довжини n. У той же час, якщо вибирати короткі блоки, то в криптограмі збережеться статистика повідомлення, що опонент може використовувати для ефективного криптоаналізу, як, наприклад, це реалізується при криптоаналізі шифру простої заміни. Для вирішення цього протиріччя звичайно вибираються підблоки помірної довжини n, потім до кожного підблоку застосовуються нелінійні перетворення і, нарешті, виконуються перестановки символів підблоків у межах усього блока довжини n.
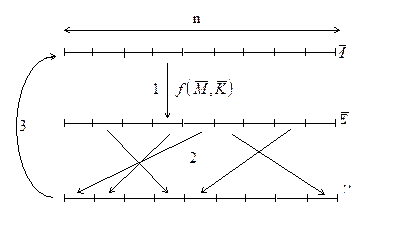 Мал. 3.5. Побудова блокових шифрів. 3.5. Побудова блокових шифрів.
Мал. 3.5. Побудова блокових шифрів. 3.5. Побудова блокових шифрів.
|
Нелінійні перетворення повинні залежати від використовуваного секретного ключа, що при повторенні перетворення (при виконанні нової ітерації) звичайно заміняється на новий, отриманий перетворенням вихідного ключа.
Найпростішим засобом завдання нелінійного перетворення є табличний засіб, коли двоїчний блок спочатку перетвориться в число, потім це число по таблиці перетвориться в інше і, нарешті, отримане число знову по таблиці перетвориться в двоїчний блок. Наприклад, шифруються блоки довжиною n = 3, яким зіставлені такі числа: 000 - 0, 001 - 1, 010 - 2, ... , 111 - 7. Тоді таблиця підстановок може бути задана в такий спосіб:
{0, 1, 2, 3, 4, 5, 6, 7}®{4, 2, 6, 7, 0, 5, 1, 3} .
Це означає, що, наприклад, вхідний блок 011 буде перетворений у вихідний блок 111. Складність такого перетворення залежить від довжини таблиці, що дорівнює 2n, де n - довжина блока.
Вигляд нелінійного перетворення звичайно залежить від певних біт розширеного ключа, що виробляється з вихідного ключа. Наприклад, нелінійне перетворення, що залежить від біт розширеного ключа  = (K1,K2,K3), може мати вигляд
= (K1,K2,K3), може мати вигляд
f( ,
, ) = f((K1,K2,K3),(M1,M2,M3) ) =
) = f((K1,K2,K3),(M1,M2,M3) ) =  = (E1, E2, E3).
= (E1, E2, E3).
E1= K1K2M1M2, E2 = K2K3M2M3,
E3 = (K1Å K2)M1M3, 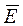 = (E1, E2, E3). (3.3)
= (E1, E2, E3). (3.3)
Якщо криптограма 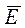 і повідомлення
і повідомлення  = (M1, M2, M3) відомі, то при виконанні криптоаналізу можна скласти рівняння щодо елементів розширеного ключа
= (M1, M2, M3) відомі, то при виконанні криптоаналізу можна скласти рівняння щодо елементів розширеного ключа 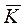 . Це буде система нелінійних рівнянь із невідомими K1, K2, K3, де дії виконуються по модулю два.
. Це буде система нелінійних рівнянь із невідомими K1, K2, K3, де дії виконуються по модулю два.
У процесі шифрування часто виконується декілька перетворень із двоїчними блоками, при чому, крім лінійної операції додавання по модулю два, використовуються, наприклад, операції додавання по модулю 2n, 2n+1 або множення по модулю 2n+1, де n - довжина блока і т.п. Тому криптоаналіз гарного блокового шифру не зводиться до відомих поліноміальних задач.
Більшість сучасних блокових шифрів реалізується на основі, так називаної, структури Файстеля. Для цього попередньо з вихідного ключа 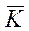 =
= 0 за допомогою заданого детермінованого перетворення, що входить в опис алгоритму шифрування, формується послідовність розширених ключів
0 за допомогою заданого детермінованого перетворення, що входить в опис алгоритму шифрування, формується послідовність розширених ключів 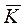 i, i = 1,2,...,d, де d - число ітерацій.
i, i = 1,2,...,d, де d - число ітерацій.
 Мал. 3.6. Підготовка блоків для шифрування на основі структури Файстеля
Мал. 3.6. Підготовка блоків для шифрування на основі структури Файстеля
|
Далі структура Файстеля припускає такий засіб перетворення блоків. Спочатку послідовність двоїчних символів повідомлення розбивається на блоки довжиною n=2n0 (мал. 3.6).
Кожний з отриманих блоків шифрується однаково з використанням такого рекурентного співвідношення , що на i-му кроці має вигляд
 ,
,
i=2,3,...,d , (3.4)
де  0 і
0 і  1 - підблоки першого блока вихідного повідомлення, f( , ) - детермінована відкрита нелінійна функція,
1 - підблоки першого блока вихідного повідомлення, f( , ) - детермінована відкрита нелінійна функція, 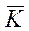 i-1 - елементи послідовності розширених ключів, сформовані детермінованим способом з основного секретного ключа
i-1 - елементи послідовності розширених ключів, сформовані детермінованим способом з основного секретного ключа 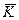 даної криптосистеми. Криптограма, сформована на останній ітерації d, приймає вигляд
даної криптосистеми. Криптограма, сформована на останній ітерації d, приймає вигляд
 = (
= ( d - 1,
d - 1, d). (3.5)
d). (3.5)
Наприклад, якщо дано  = (
= ( 0,
0, 1), то обчислюємо
1), то обчислюємо
 2 =
2 =  0 Å f(
0 Å f(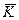 1,
1,  1),
1),
складаємо ( 1,
1, 2), знову обчисляємо
2), знову обчисляємо
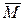 3 =
3 = 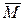 1 Å f(
1 Å f(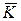 2,
2, 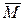 2),
2),
складаємо ( 2,
2, 3) і т.д., ..., до отримання послідовностей
3) і т.д., ..., до отримання послідовностей  d - 1 і
d - 1 і  d, із котрих і формується криптограма
d, із котрих і формується криптограма  = (
= (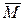 d - 1,
d - 1,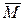 d).
d).
Перевага такої структури складається в тому, що по-перше, для неї виконується принцип перемішування між підблоками, по-друге, дуже просто реалізується алгоритм дешифрування при ключі, відомому законному користувачу. При цьому важливо те, що функція f( , ) навіть не обов'язково повинна мати обернену! Дійсно, коректне дешифрування в даній структурі виконується по тому ж алгоритмі, що і шифрування: Нехай  = (
= ( 0,
0, 1) = (
1) = ( d - 1,
d - 1, d).
d).
Тоді
 ,... ,
,... , 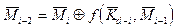 ,... ,
,... ,
 1 =
1 = 3 Å f(
3 Å f(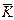 2 ,
2 , 2 ),
2 ),  0 =
0 = 2 Å f(
2 Å f(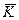 1 ,
1 , 1 ),
1 ),
 = (
= ( 0,
0, 1), що, як очевидно і збігається з вихідним повідомленням.
1), що, як очевидно і збігається з вихідним повідомленням.
Є багато різноманітних блокових шифрів, заснованих на структурі Файстеля, що відрізняються вибором функції f і засобом формування розширених ключів 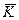 i i=1,2,…,d з основного ключа
i i=1,2,…,d з основного ключа 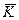 . Нехай на такий шифр відбувається напад із відомим повідомленням. Тоді, знаючи опис функції f і засіб побудови підключей по основному ключу, опонент може скласти систему нелінійних рівнянь і спробувати її вирішити щодо ключа як невідомого. Стійкість даного типу шифрів грунтується на складності рішення системи нелінійних рівнянь із діями по модулі два. Доведено, що в загальному випадку ця задача відноситься до класу NP - важких задач.
. Нехай на такий шифр відбувається напад із відомим повідомленням. Тоді, знаючи опис функції f і засіб побудови підключей по основному ключу, опонент може скласти систему нелінійних рівнянь і спробувати її вирішити щодо ключа як невідомого. Стійкість даного типу шифрів грунтується на складності рішення системи нелінійних рівнянь із діями по модулі два. Доведено, що в загальному випадку ця задача відноситься до класу NP - важких задач.
1.2.2 Багатократне шифрування блоків
На перший погляд представляється очевидним, що можна значно підвищити стійкість шифру, якщо криптограму, отриману за допомогою ключа 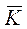 1, зашифрувати ще раз за допомогою іншого ключа
1, зашифрувати ще раз за допомогою іншого ключа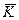 2, тобто реалізувати процедури шифрування-дешифрування в такий спосіб:
2, тобто реалізувати процедури шифрування-дешифрування в такий спосіб:
 ,
, 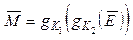 . (3.6)
. (3.6)
Проте, нескладно показати, що якщо довжина ключа дорівнює N, те фактично застосування дворазового шифрування збільшує число операцій, необхідних при криптоаналізі за допомогою тотального перебору ключів від 2N до 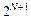 . Іншими словами, обсяг перебору збільшується тільки в два рази і, отже, дворазове шифрування не є ефективним.
. Іншими словами, обсяг перебору збільшується тільки в два рази і, отже, дворазове шифрування не є ефективним.
Метод, що у даному випадку використовується для дешифрування, називається «зустріччю в центрі». Нехай є криптограма  , отримана шляхом повторного шифрування.
, отримана шляхом повторного шифрування.
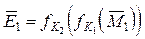 (3.7)
(3.7)
Для криптоаналізу використовуємо напад із відомим повідомленням, рахуючи, що відомо не менше двох блоків повідомлення і відповідні їм блоки криптограми, наприклад,
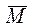 1®
1®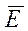 1 і
1 і 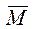 2®
2®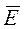 2. (3.8)
2. (3.8)
Рішення задачі будемо шукати шляхом перебору всіх можливих двоїчних ключів 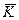 довжини N. Варіанти ключа помістимо в перший рядок заздалегідь складеної таблиці. В другий рядок таблиці помістимо результати шифрування першого відомого блока повідомлення
довжини N. Варіанти ключа помістимо в перший рядок заздалегідь складеної таблиці. В другий рядок таблиці помістимо результати шифрування першого відомого блока повідомлення 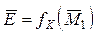 відповідними варіантами ключів, а в третю - результати дешифрування першого блока криптограми, отримані як
відповідними варіантами ключів, а в третю - результати дешифрування першого блока криптограми, отримані як 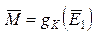 .
.
| Варіант ключа K
| K1
| K2
|
|
|
| Km
|
| Kn
|
| 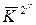
|
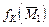
| E1
| E2
|
|
|
| Em
|
|
|
| 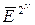
|
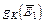
| M1
| M2
|
|
|
|
|
| Mn
|
| 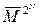
|
З співвідношення  очевидно, що для дійсно використаних ключів
очевидно, що для дійсно використаних ключів 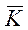 1або
1або 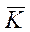 2 якийсь елемент Em другого рядка повинний обов'язково співпасти з яким-небудь елементом Mn третього рядка. У такий спосіб достатньо знайти збіжні елементи в другому і третьому рядках і вибрати відповідні їм ключі Km і Kn у якості кандидатів у дійсні ключі
2 якийсь елемент Em другого рядка повинний обов'язково співпасти з яким-небудь елементом Mn третього рядка. У такий спосіб достатньо знайти збіжні елементи в другому і третьому рядках і вибрати відповідні їм ключі Km і Kn у якості кандидатів у дійсні ключі 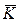 1 і
1 і 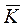 2. Проте збіги можливі і не тільки для істинних ключів, тобто кандидатів може виявитися декілька. Тому потрібно спробувати застосувати знайдені ключі до іншої пари повідомлення-криптограми для перевірки другого співвідношення
2. Проте збіги можливі і не тільки для істинних ключів, тобто кандидатів може виявитися декілька. Тому потрібно спробувати застосувати знайдені ключі до іншої пари повідомлення-криптограми для перевірки другого співвідношення
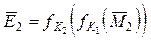 . (3.9)
. (3.9)
Якщо виповниться і ця рівність то, як правило, знайдені ключі називаються істинними.
Для підвищення стійкості шифрування використовують не подвійне, а потрійне шифрування на трьох різноманітних ключах, тобто формують криптограму по такому правилу
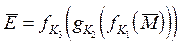 ,
, 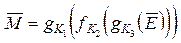 . (3.10)
. (3.10)
Доводиться, що найкращий можливий метод криптоаналізу за допомогою тотального перебору ключів зажадає в цьому випадку 22N кроків, тобто стійкість криптограми істотно збільшується.
1.2.3 Основні параметри і принципи побудови


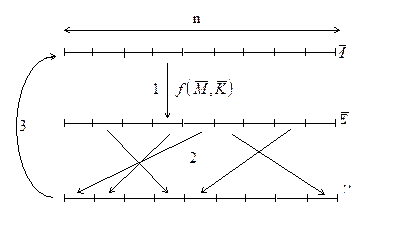 Мал. 3.5. Побудова блокових шифрів. 3.5. Побудова блокових шифрів.
Мал. 3.5. Побудова блокових шифрів. 3.5. Побудова блокових шифрів.
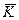 = (K1,K2,K3), може мати вигляд
= (K1,K2,K3), може мати вигляд ) = f((K1,K2,K3),(M1,M2,M3) ) =
) = f((K1,K2,K3),(M1,M2,M3) ) = 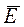 = (E1, E2, E3).
= (E1, E2, E3).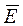 = (E1, E2, E3). (3.3)
= (E1, E2, E3). (3.3)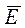 і повідомлення
і повідомлення 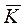 . Це буде система нелінійних рівнянь із невідомими K1, K2, K3, де дії виконуються по модулю два.
. Це буде система нелінійних рівнянь із невідомими K1, K2, K3, де дії виконуються по модулю два.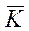 =
= 0 за допомогою заданого детермінованого перетворення, що входить в опис алгоритму шифрування, формується послідовність розширених ключів
0 за допомогою заданого детермінованого перетворення, що входить в опис алгоритму шифрування, формується послідовність розширених ключів  Мал. 3.6. Підготовка блоків для шифрування на основі структури Файстеля
Мал. 3.6. Підготовка блоків для шифрування на основі структури Файстеля
 ,
, = (
= (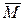 3 =
3 = 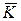 2,
2,  = (
= ( ,... ,
,... , 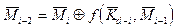 ,... ,
,... ,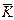 2 ,
2 ,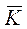 1, зашифрувати ще раз за допомогою іншого ключа
1, зашифрувати ще раз за допомогою іншого ключа ,
, 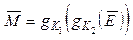 . (3.6)
. (3.6)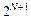 . Іншими словами, обсяг перебору збільшується тільки в два рази і, отже, дворазове шифрування не є ефективним.
. Іншими словами, обсяг перебору збільшується тільки в два рази і, отже, дворазове шифрування не є ефективним. , отримана шляхом повторного шифрування.
, отримана шляхом повторного шифрування.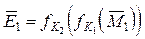 (3.7)
(3.7)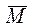 1®
1®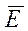 1 і
1 і 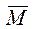 2®
2®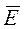 2. (3.8)
2. (3.8)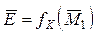 відповідними варіантами ключів, а в третю - результати дешифрування першого блока криптограми, отримані як
відповідними варіантами ключів, а в третю - результати дешифрування першого блока криптограми, отримані як 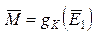 .
.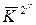
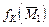
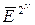
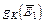
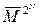
 очевидно, що для дійсно використаних ключів
очевидно, що для дійсно використаних ключів 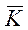 1або
1або 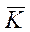 2 якийсь елемент Em другого рядка повинний обов'язково співпасти з яким-небудь елементом Mn третього рядка. У такий спосіб достатньо знайти збіжні елементи в другому і третьому рядках і вибрати відповідні їм ключі Km і Kn у якості кандидатів у дійсні ключі
2 якийсь елемент Em другого рядка повинний обов'язково співпасти з яким-небудь елементом Mn третього рядка. У такий спосіб достатньо знайти збіжні елементи в другому і третьому рядках і вибрати відповідні їм ключі Km і Kn у якості кандидатів у дійсні ключі 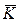 1 і
1 і 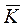 2. Проте збіги можливі і не тільки для істинних ключів, тобто кандидатів може виявитися декілька. Тому потрібно спробувати застосувати знайдені ключі до іншої пари повідомлення-криптограми для перевірки другого співвідношення
2. Проте збіги можливі і не тільки для істинних ключів, тобто кандидатів може виявитися декілька. Тому потрібно спробувати застосувати знайдені ключі до іншої пари повідомлення-криптограми для перевірки другого співвідношення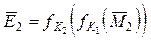 . (3.9)
. (3.9)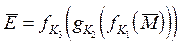 ,
, 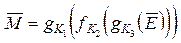 . (3.10)
. (3.10)