Слід зазначити, що не обов’язково позначати всі можливі прямокутники в діаграмі Вейча. Достатньо тільки покрити всі одиниці хоча б один раз. Наприклад, у розглянутому прикладі в таблиці для функції  можна ще виділити прямокутник, що відповідає імпліканті
можна ще виділити прямокутник, що відповідає імпліканті 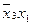 , але ця імпліканта є зайвою, бо всі одиниці зазначеного прямокутника вже належать іншим прямокутникам.
, але ця імпліканта є зайвою, бо всі одиниці зазначеного прямокутника вже належать іншим прямокутникам.
Сусідні клітинки можуть бути розташовані у протилежних рядках (колонках) таблиці (див. наступний приклад).
Приклад. Виконати мінімізацію перемикальних функцій  трьох аргументів, заданих таблицею істинності за допомогою діаграм Вейча.
трьох аргументів, заданих таблицею істинності за допомогою діаграм Вейча.
Таблиця істинності
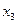  
| 
| 
| 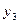
|
| 0 0 0
0 0 1
0 1 0
0 1 1
1 0 0
1 0 1
1 1 0
1 1 1
|
|
|
|
Заповнимо діаграми Вейча і знайдемо мінімальну кількість прямокутників максимального розміру, що покривають усі одиниці (рис. ).
У результаті отримаємо МДНФ функцій 
 :
:
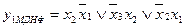 ;
;
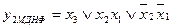 ;
;
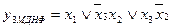 .
.
Приклад. За допомогою метода Вейча виконати мінімізацію перемикальної функції чотирьох аргументів, заданої ДНФ загального вигляду
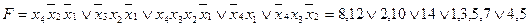 .
.
Числами визначені номери наборів. Які відповідають одиничним значенням конституенти та імплікант.
Заповнимо діаграму Вейча і знайдемо мінімальну кількість прямокутників максимального розміру, що покривають ядро функції (рис. )
Ядро функції, як видно із діаграми, складає множина імплікант 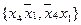 , бо покрити ці імпліканти іншими прямокутниками на чотири клітинки неможливо. Кожну з одиниць, що залишилися непокритими (одиниці в клітинках з номерами 2 і 4 позначені зірочками). Можна об’єднати з сусідніми клітинками двома різними способами, відміченими пунктиром. Таким чином, можна обрати як МДНФ одну з чотирьох наступних ТДНФ:
, бо покрити ці імпліканти іншими прямокутниками на чотири клітинки неможливо. Кожну з одиниць, що залишилися непокритими (одиниці в клітинках з номерами 2 і 4 позначені зірочками). Можна об’єднати з сусідніми клітинками двома різними способами, відміченими пунктиром. Таким чином, можна обрати як МДНФ одну з чотирьох наступних ТДНФ:
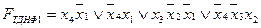 ;
;
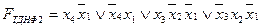 ;
;
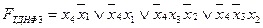 ;
;
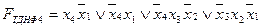 .
.
Даний метод дає можливість одержувати мінімальні ДНФ булевої функції  . В його основу покладено задавання функцій діаграмами деякого спеціального вигляду, так званими діаграмами (картами) Вейча чи Карно. Для булевої функції двох змінних ці діаграми мають вигляд (рис. 1. 9, а):
. В його основу покладено задавання функцій діаграмами деякого спеціального вигляду, так званими діаграмами (картами) Вейча чи Карно. Для булевої функції двох змінних ці діаграми мають вигляд (рис. 1. 9, а):
Діаграми (карти) Вейча Діаграми (карти) Карно
Рис. 1. 9. Діаграми (карти) Вейча і Карно: а) для двох змінних;
б) для трьох змінних; в) для чотирьох змінних.
Кожна клітинка діаграми відповідає набору змінних булевої функції в її таблиці істиності. На рис. 1. 9 показана ця відповідність. Якщо булева функція приймає одиничне значення на деякому наборі, в клітинці діаграми, що відповідає даному набору, ставиться одиниця. Нульові значення булевої функції в діаграмі не ставляться. Для булевої функції трьох змінних діаграми Вейча та Карно мають вигляд, показаний на рис. 1. 9, б. Додавання до неї ще такої ж таблиці дає діаграму для функції 4-х змінних (рис. 1. 9, в). Таким же чином, тобто приписуванням ще одної діаграми 4-х змінних до щойно розглянутої, можна одержати діаграму для функції 5-ти змінних і т. д. Однак діаграми для функцій з числом змінних більше 4-х застосовуються рідко.
Для діаграм Вейча (чи Карно) властиве наступне:
- кожній клітинці діаграми відповідає свій набір;
- сусідні набори розташовані поряд в рядку чи в стовпці.
Сусідніми називаються набори, що відрізняються одною компонентою. Нагадаємо, що конституенти, відповідні таким наборам, склеюються. Наприклад, для функції, заданої табл. 1. 15, конституенти, відповідні парі одиниць в стовпці лівої частини діаграми склеюються і породжують елементарний добуток із 2-х букв:

Таблиця 1. 15
Стовпці, розташовані на краях діаграми, теж
вважаються сусідніми:
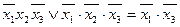
Відзначимо, що одержуваний елементарний добуток легко визначити одразу по діаграмі: це добуток змінних, що приймають одне й те ж значення в обох клітинках.
Для нашого прикладу наявне ще одне склеювання для пари одиниць в лівій частині діаграми. В результаті даного склеювання одержуємо елементарний добуток 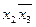 :
: 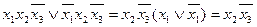 . Із розглянутих раніше методів мінімізації нам відомо, що можливе подальше склеювання одержуваних елементарних добутків. На діаграмах Вейча чи Карно вони також розташовуються поряд.
. Із розглянутих раніше методів мінімізації нам відомо, що можливе подальше склеювання одержуваних елементарних добутків. На діаграмах Вейча чи Карно вони також розташовуються поряд.
Отже, загальне правило склеювання на діаграмах Вейча чи Карно можна сформулювати таким чином: склеюванню підлягають прямокутні конфігурації (контури), заповнені одиницями, і які містять число клітинок, що дорівнює 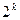 , де
, де 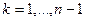 . Одержуваний новий елементарний добуток визначається як добуток змінних, що не змінюють свого значення на всіх склеюваних наборах.
. Одержуваний новий елементарний добуток визначається як добуток змінних, що не змінюють свого значення на всіх склеюваних наборах.
Мінімізація булевої функції полягає в знаходженні мінімального накриття всіх одиниць діаграми блоками із одиниць, розташованих у сусідніх клітинках діаграми. При цьому завжди вважається, що лівий край діаграми
4-х змінних притикається до її правого краю, а верхній край діаграми притикається до нижнього її краю. Після одержання мінімального накриття всіх одиниць діаграми мінімальна ДНФ булевої функції записується як диз’юнкція елементарних кон’юнкцій, що відповідають вилученим блокам одиниць в діаграмі.
Розглянемо кілька прикладів.
Приклад 1. Булева функція  має ДДНФ вигляду
має ДДНФ вигляду
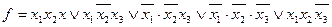 .
.
Знайти мінімальну ДНФ за допомогою діаграми Вейча.
Діаграма Вейча, відповідна функції  представлена в табл. 1. 16. В
представлена в табл. 1. 16. В
даному випадку мінімальне накриття всіх
Таблиця 1. 16 одиниць діаграми можливе тільки блоками по
дві одиниці. Кожному такому блоку відповідає
своя кон’юнкція:
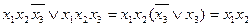 ;
;
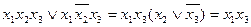 ;
;
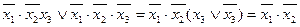 .
.
Отже, мінімальна ДНФ функції має вигляд:
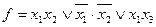 .
.
Очевидно, проста імпліканта 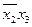 не потрібна для одержання МДНФ.
не потрібна для одержання МДНФ.
Приклад 2. Булеві функції 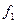 ,
, 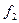 ,
, 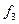 ,
, 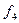 ,
, 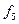 ,
, 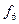 задані таблицею істиності (табл. 1. 17). Знайти їх мінімальні ДНФ.
задані таблицею істиності (табл. 1. 17). Знайти їх мінімальні ДНФ.
Таблиця 1. 17
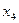 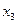  
| 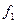
| 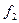
| 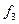
| 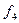
| 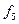
| 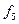
|
| 0 0 0 0
0 0 0 1
0 0 1 0
0 0 1 1
0 1 0 0
0 1 0 1
0 1 1 0
0 1 1 1
1 0 0 0
1 0 0 1
1 0 1 0
1 0 1 1
1 1 0 0
1 1 0 1
1 1 1 0
1 1 1 1
|
|
|
|
|
|
|
Записуємо одиниці у клітинки діаграм Вейча, котрі відповідають наборам, на яких функції 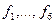 приймають значення 1. Діаграми Вейча булевих функцій зображені на рис. 1. 10, там же показані мінімальні
приймають значення 1. Діаграми Вейча булевих функцій зображені на рис. 1. 10, там же показані мінімальні
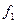
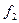
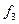
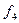
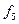
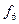
Рис. 1. 10. Діаграми Вейча булевих функцій 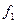 ,
, 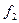 ,
, 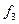 ,
, 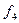 ,
, 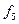 ,
, 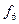 .
.
накриття одиниць для кожної функції. Для функції 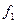 мінімальне накриття всіх одиниць діаграми можливе двома блоками: блоком з двох одиниць і блоком з чотирьох одиниць. Кон’юнкції, що відповідають цим блокам дорівнюють
мінімальне накриття всіх одиниць діаграми можливе двома блоками: блоком з двох одиниць і блоком з чотирьох одиниць. Кон’юнкції, що відповідають цим блокам дорівнюють  і
і 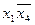 відповідно, а МДНФ функції має вигляд:
відповідно, а МДНФ функції має вигляд:

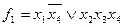 .
.
Мінімальне накриття всіх одиниць діаграми для функції 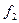 можливе за допомогою п’яти блоків (три блоки по дві одиниці, один блок з чотирьох одиниць і один блок з однієї одиниці). Кон’юнкції, що відповідають цим блокам і МДНФ даної функції мають вигляд:
можливе за допомогою п’яти блоків (три блоки по дві одиниці, один блок з чотирьох одиниць і один блок з однієї одиниці). Кон’юнкції, що відповідають цим блокам і МДНФ даної функції мають вигляд: 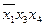 ,
,  ,
, 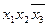 ,
,  ,
, 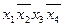 ,
,  .
.
Для функції 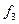 мінімальне накриття всіх одиниць діаграми можливе двома блоками по чотири одиниці в кожному. Конституенти, що відповідають цим блокам і мінімальна ДНФ функції мають вигляд:
мінімальне накриття всіх одиниць діаграми можливе двома блоками по чотири одиниці в кожному. Конституенти, що відповідають цим блокам і мінімальна ДНФ функції мають вигляд: 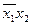 ,
, 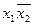 ;
; 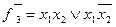 .
.
Мінімальне накриття всіх одиниць діаграми функції 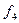 можливе трьома блоками: блоком з двох одиниць і двома блоками з чотирьох одиниць кожний. Мінімальна ДНФ має вигляд:
можливе трьома блоками: блоком з двох одиниць і двома блоками з чотирьох одиниць кожний. Мінімальна ДНФ має вигляд: 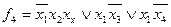 .
.
Для функції 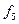 мінімальне накриття всіх одиниць на діаграмі Вейча здійснюється двома блоками по вісім одиниць кожний. Мінімальна ДНФ має вигляд:
мінімальне накриття всіх одиниць на діаграмі Вейча здійснюється двома блоками по вісім одиниць кожний. Мінімальна ДНФ має вигляд: 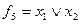 .
.
Мінімальне накриття всіх одиниць на діаграмі Вейча функції 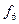 здійснюється трьома блоками: один блок із двох одиниць і два блоки із чотирьох одиниць. Мінімальна ДНФ функції має вигляд:
здійснюється трьома блоками: один блок із двох одиниць і два блоки із чотирьох одиниць. Мінімальна ДНФ функції має вигляд:
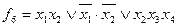 .
.
З наведених прикладів видно, що кожній імпліканті функції відповідає на діаграмі прямокутник, котрий містить 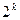 клітинок з одиницями (
клітинок з одиницями (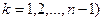 .
.
Чим більше клітинок містить прямокутник, тим менше букв входить у представлення імпліканти. Імпліканта містить тільки ті змінні, котрі приймають однакове значення для всіх клітинок прямокутника.
Отже, в загальному випадку для мінімізації булевих функцій за допомогою діаграм (карт) Вейча чи Карно необхідно:
- одержати ДДНФ заданої функції;
- згідно таблиці істиності даної функції нанести одиниці на діаграму (карту) Вейча чи Карно;
- об’єднати сусідні одиниці діаграми в блоки для одержання мінімального накриття всіх одиниць на діаграмі;
- здійснити спрощення, вилучаючи компоненти, котрі доповнюють один одного всередині блока (здійснити операцію склеювання);
- об’єднати одержані елементарні імпліканти (по одній у кожному блоці) операцією АБО.
Одержаний в результаті цих дій вираз і є не що інше як мінімальна ДНФ булевої функції.
1. 4. 5. Дужкова мінімізація булевих функцій
Розглянуті методи мінімізації булевих функцій дозволяють одержати мінімальну ДНФ. В деяких випадках мінімальна ДНФ піддається подальшому спрощенню за рахунок винесення за дужки спільних компонентів. Така операція називається дужковою мінімізацією або факторизацією булевих функцій. Процес факторизації описується за допомогою факторного алгоритму.
Розглянемо процес факторизації булевої функції на прикладі.
Приклад. Допустимо, що мінімальна ДНФ функції  має вигляд:
має вигляд:
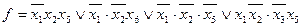 .
.
Позначимо кожну кон’юнкцію, що входить в  , буквами
, буквами  ,
, 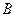 ,
, 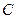 ,
,  відповідно:
відповідно: 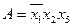 ;
; 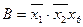 ;
; 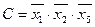 ;
; 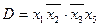 .
.
Знайдемо спільні компоненти всіх можливих пар кон’юнкцій:
( ,
, 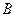 ) -
) - 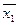 ; (
; ( ,
, 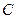 ) -
) - 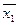 ; (
; ( ,
,  ) -
) - 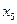 ; (
; (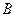 ,
, 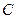 ) -
) - 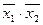 ; (
; (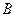 ,
,  ) -
) - 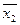 ;
;
(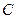 ,
,  ) -
) - 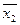 . Пара (
. Пара ( 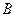 ,
, 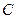 ) має найбільше спільних компонентів (
) має найбільше спільних компонентів (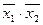 ). Запишемо мінімальну ДНФ функції, винісши за дужки тільки
). Запишемо мінімальну ДНФ функції, винісши за дужки тільки 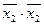 в парі кон’юнкцій (
в парі кон’юнкцій (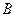 ,
, 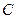 ):
):
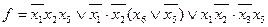 .
.
Позначимо утворені кон’юнкції МДНФ функції  буквами
буквами 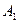 ,
,  ,
, 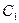 :
:
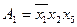 ;
;  ;
; 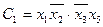 .
.
Знайдемо спільні компоненти всіх можливих пар кон’юнкцій:
(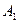 ,
,  ) -
) - 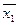 ; (
; (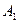 ,
, 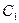 ) -
) - 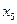 ; (
; ( ,
, 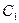 ) -
) - 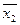 .
.
Довжина спільних компонентів однакова, тому в цьому разі можна вибрати один із можливих варіантів:
 .
.
Порівняння одержаної дужкової форми функції  з вихідною показує, що число входжень змінних в формулу зменшилось.
з вихідною показує, що число входжень змінних в формулу зменшилось.
На практиці зустрічаються автомати, що мають декілька виходів. Вони описуються системою функцій 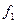 ,
, 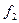 , ...,
, ..., 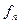 , де
, де 
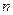 - число різних виходів. Виникає задача сумісної мінімізації даних функцій, котра може бути розв’язана за два етапи. Спочатку спрощується кожна функція окремо, а потім вилучається спільна частина всіх функцій, для реалізації котрої будується спеціальна схема. Сигнали з виходу останньої подаються на входи інших схем, що виробляють ту чи іншу функцію. Однак таке спрощення приводить до збільшення числа ступенів (ярусів) автомата, що зменшує його швидкодію.
- число різних виходів. Виникає задача сумісної мінімізації даних функцій, котра може бути розв’язана за два етапи. Спочатку спрощується кожна функція окремо, а потім вилучається спільна частина всіх функцій, для реалізації котрої будується спеціальна схема. Сигнали з виходу останньої подаються на входи інших схем, що виробляють ту чи іншу функцію. Однак таке спрощення приводить до збільшення числа ступенів (ярусів) автомата, що зменшує його швидкодію.
1. 4. 6. Мінімізація частково визначених функцій
У реальних системах можливі випадки, коли не всі набори змінних подаються на входи комбінаційної схеми, тобто існують заборонені вхідні комбінації змінних. На таких наборах перемикальна функція вважається невизначеною, що дає додаткові можливості для спрощення комбінаційної схеми.
У таблиці істинності невизначені значення функції позначаються довільним символом, відмінним від 0 і 1, наприклад – прочерком.
Мінімізацію частково визначених функцій можна здійснювати будь-яким з наведених вище методів мінімізації. Для забезпечення найефективнішої мінімізації доцільно провести до визначення перемикальної функції на заборонених наборах таким чином, щоб спростити функцію за рахунок більших можливостей склеювання.
Мінімізація частково визначених функцій методом Вейча
Під час використання метода Вейча прочерки розглядають як одиниці в тих випадках, коли це приводить до збільшення розміру прямокутника, що відповідає імпліканті. В протилежному випадку прочерки розглядаються як нулі.
Приклад. Виконати мінімізацію перемикальної функції, заданої діаграмою Вейча (рис. 2.6).
Для визначення мінімальної форми запису функції замінюємо певні прочерки одиницями для збільшення розміру прямокутників, тобто отримання імплікант з меншою кількістю букв. Значення функції на наборі 1101, який не увійшов в прямокутники, вважаємо рівним нулю.
Диз’юнкція визначених простих імплікант дає МДНФ до визначеної перемикальної функції
 .
.
Мінімізація частково визначених функцій аналітичними методами
Під час використання аналітичних методів, таких як методи Квайна та Квайна – Мак-Класкі, виконуються ті самі етапи мінімізації, що й для повністю визначених функцій.
Особливістю мінімізації частково визначених функцій в диз’юнктивних формах булевої алгебри складається з того, що перед початком мінімізації у ДДНФ перемикальної функції вводять усі конституенти заборонених наборів, тобто до визначають функцію на цих наборах одиничним значенням.
Далі виконують стандартні процедури мінімізації, але під час побудови таблиці покриття конституенти заборонених наборів не включають у заголовки стовпців таблиці покриття.
Приклад. Виконати мінімізацію частково визначеної перемикальної функції, що задана таблицею істинності (табл. ), методом Квайна.
Таблиця
Таблиця істинності
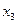  
| 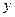
|
| 0 0 0
0 0 1
0 1 0
0 1 1
1 0 0
1 0 1
1 1 0
1 1 1
|
−
−
−
−
|
Без урахування наборів, на яких функція невизначена, маємо
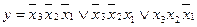 .
.
Після доповнення конституентами одиниці, що відповідають забороненим наборам (помічені зірочками), аналітичний запис функції приймає вигляд
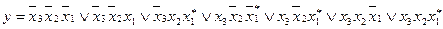 .
.
Для наглядності процесу мінімізації конституенти та імпліканти записуємо стовпцями. У дужках для конституент вказуємо їх номери, а для імплікант – номери конституент, що склеювалися. Терми, що поглинаються, викреслюємо.
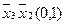
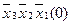
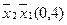
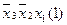
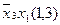
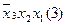
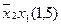
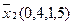
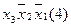
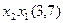
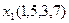
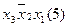
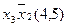
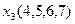
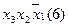
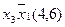
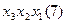

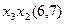
(закреслюються перші два стовпці)
Виконавши всі можливі склеювання та поглинання, одержуємо СДНФ заданої перемикальної функції, що довизначена на заборонених наборах:
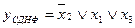 .
.
Але таке довизначення перемикальної функції на заборонених наборах можливо не є оптимальним. Для перевірки цього будуємо таблицю покриття (табл. 2. 15), в яку включаємо тільки ті конституенти одиниці. Котрі відповідають наперед визначеним одиничним значенням заданої перемикальної функції.
Таблиця 2. 15
Таблиця покриття
Виходячи з таблиці покриття знаходимо ТДНФ перемикальної функції, яка є її мінімальною МДНФ:
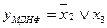 .
.
Мінімізація систем частково визначених функцій
Під час мінімізації систем частково визначених функцій використовується такий саме підхід, як і під час мінімізації окремих частково визначених функцій. На заборонених наборах значення функцій вважається одиничним, але на етапі вибору конституенти, що відповідають забороненим наборам, не включаються в таблицю покриття.
Приклад. Виконати мінімізацію системи частково визначених перемикальних функцій, заданих таблицею істинності (табл. ), методом Квайна – Мак-Класкі.
Таблиця
Параметри функцій
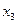  
| 
| 
| 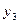
|
| 0 0 0
0 0 1
0 1 0
0 1 1
1 0 0
1 0 1
1 1 0
1 1 1
| −
−
|
−
−
| −
|
Виписуємо 0-куби, що відповідають забороненим наборам і наборам, на яких функції приймають одиничне значення. При цьому позначаємо належність конституент до заданих функцій. Виконуємо всі можливі склеювання і поглинання:
X00(1, 2, 3)
− − − − − − − X01(2)


 можна ще виділити прямокутник, що відповідає імпліканті
можна ще виділити прямокутник, що відповідає імпліканті 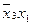 , але ця імпліканта є зайвою, бо всі одиниці зазначеного прямокутника вже належать іншим прямокутникам.
, але ця імпліканта є зайвою, бо всі одиниці зазначеного прямокутника вже належать іншим прямокутникам. трьох аргументів, заданих таблицею істинності за допомогою діаграм Вейча.
трьох аргументів, заданих таблицею істинності за допомогою діаграм Вейча.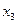



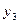

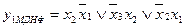 ;
;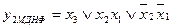 ;
;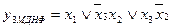 .
.
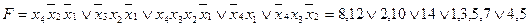 .
.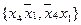 , бо покрити ці імпліканти іншими прямокутниками на чотири клітинки неможливо. Кожну з одиниць, що залишилися непокритими (одиниці в клітинках з номерами 2 і 4 позначені зірочками). Можна об’єднати з сусідніми клітинками двома різними способами, відміченими пунктиром. Таким чином, можна обрати як МДНФ одну з чотирьох наступних ТДНФ:
, бо покрити ці імпліканти іншими прямокутниками на чотири клітинки неможливо. Кожну з одиниць, що залишилися непокритими (одиниці в клітинках з номерами 2 і 4 позначені зірочками). Можна об’єднати з сусідніми клітинками двома різними способами, відміченими пунктиром. Таким чином, можна обрати як МДНФ одну з чотирьох наступних ТДНФ: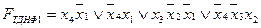 ;
;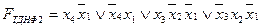 ;
;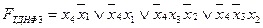 ;
;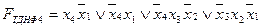 .
. . В його основу покладено задавання функцій діаграмами деякого спеціального вигляду, так званими діаграмами (картами) Вейча чи Карно. Для булевої функції двох змінних ці діаграми мають вигляд (рис. 1. 9, а):
. В його основу покладено задавання функцій діаграмами деякого спеціального вигляду, так званими діаграмами (картами) Вейча чи Карно. Для булевої функції двох змінних ці діаграми мають вигляд (рис. 1. 9, а):
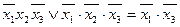
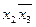 :
: 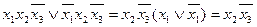 . Із розглянутих раніше методів мінімізації нам відомо, що можливе подальше склеювання одержуваних елементарних добутків. На діаграмах Вейча чи Карно вони також розташовуються поряд.
. Із розглянутих раніше методів мінімізації нам відомо, що можливе подальше склеювання одержуваних елементарних добутків. На діаграмах Вейча чи Карно вони також розташовуються поряд.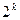 , де
, де 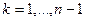 . Одержуваний новий елементарний добуток визначається як добуток змінних, що не змінюють свого значення на всіх склеюваних наборах.
. Одержуваний новий елементарний добуток визначається як добуток змінних, що не змінюють свого значення на всіх склеюваних наборах.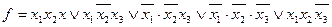 .
.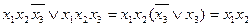 ;
;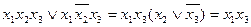 ;
;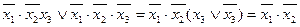 .
.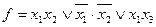 .
.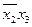 не потрібна для одержання МДНФ.
не потрібна для одержання МДНФ.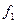 ,
, 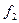 ,
, 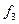 ,
, 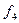 ,
, 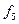 ,
, 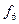 задані таблицею істиності (табл. 1. 17). Знайти їх мінімальні ДНФ.
задані таблицею істиності (табл. 1. 17). Знайти їх мінімальні ДНФ. 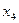
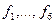 приймають значення 1. Діаграми Вейча булевих функцій зображені на рис. 1. 10, там же показані мінімальні
приймають значення 1. Діаграми Вейча булевих функцій зображені на рис. 1. 10, там же показані мінімальні і
і 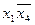 відповідно, а МДНФ функції має вигляд:
відповідно, а МДНФ функції має вигляд: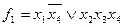 .
.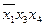 ,
,  ,
, 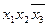 ,
,  ,
, 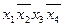 ,
,  .
.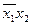 ,
, 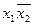 ;
; 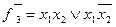 .
.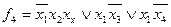 .
.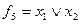 .
.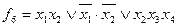 .
.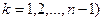 .
.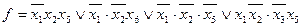 .
. ,
, 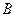 ,
, 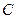 ,
,  відповідно:
відповідно: 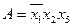 ;
; 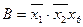 ;
; 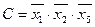 ;
; 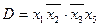 .
.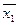 ; (
; (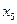 ; (
; (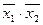 ; (
; (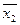 ;
;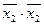 в парі кон’юнкцій (
в парі кон’юнкцій (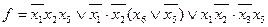 .
.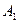 ,
,  ,
, 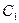 :
: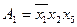 ;
;  ;
; 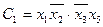 .
. .
.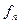 , де
, де 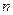 - число різних виходів. Виникає задача сумісної мінімізації даних функцій, котра може бути розв’язана за два етапи. Спочатку спрощується кожна функція окремо, а потім вилучається спільна частина всіх функцій, для реалізації котрої будується спеціальна схема. Сигнали з виходу останньої подаються на входи інших схем, що виробляють ту чи іншу функцію. Однак таке спрощення приводить до збільшення числа ступенів (ярусів) автомата, що зменшує його швидкодію.
- число різних виходів. Виникає задача сумісної мінімізації даних функцій, котра може бути розв’язана за два етапи. Спочатку спрощується кожна функція окремо, а потім вилучається спільна частина всіх функцій, для реалізації котрої будується спеціальна схема. Сигнали з виходу останньої подаються на входи інших схем, що виробляють ту чи іншу функцію. Однак таке спрощення приводить до збільшення числа ступенів (ярусів) автомата, що зменшує його швидкодію. .
.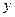
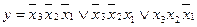 .
.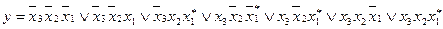 .
.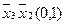
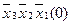
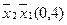
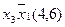
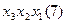

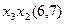
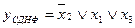 .
. .
.