Тема 1.1. Розклад визначників за елементами рядка або стовпця

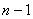Поняття визначника матриці будь-якого порядку ми введемо індукцією за порядком матриці. Це дозволяє, знаючи правило обчислення визначника матриці порядку ( ), одержати правило обчислення визначника матриці порядку 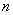. Для цього введемо поняття мінора і алгебраїчного доповнення будь-якого елемента матриці.

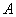Нехай – довільна квадратна матриця порядку .

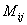Означення 1Мінором елемента 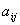матриці 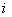порядку називається визначник матриці порядку , одержаної з матриці вилученням її -го рядка і 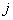-го стовпця.

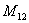Наприклад , мінором елемента 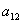матриці порядку 3 буде :

.

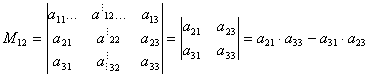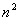Зауважимо , що матриця прядку має мінорів порядку ( ).

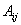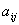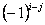
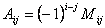
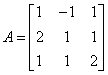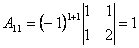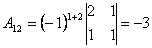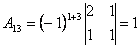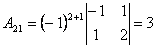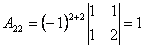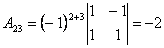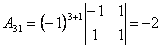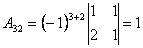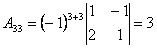Означення 2. Алгебраїчним доповненням елемента матриці порядку називається її мінор , взятий із знаком

Приклад . Обчислити алгебраїчні доповнення всіх елементів матриці

.

Розв’язання .

; ;

;

; ;

;

; ;

.

Має місце наступна основна теорема , яку подаємо без доведення .

Теорема. Визначник квадратної матриці дорівнює сумі добутків елементів будь-якого рядка чи стовпця на їх алгебраїчне доповнення

(1.15)

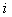(розклад за елементами -го рядка; );

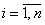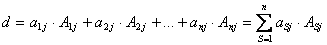(1.16)

(розклад за елементами -го стовпця; );