Розглянемо мінімізацію функції за методом Квайна на прикладі.
Приклад. Допустимо, що ДДНФ функції має вигляд:
 .
.
1 2 3 4 5 6
Для зручності викладок позначимо кожну конституанту одиниці із ДДНФ функції  яким-небудь десятковим номером.
яким-небудь десятковим номером.
Виконуємо попарне склеювання конституент одиниці відповідно до співвідношення неповного склеювання (1. 7):
1 – 2 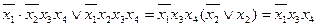 - по
- по  ;
;
1 – 5 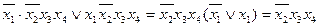 - по
- по  ;
;
2 – 6 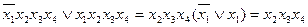 - по
- по  ;
;
3 – 4 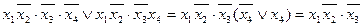 - по
- по 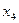 ;
;
4 – 5 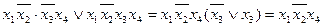 - по
- по 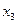 ;
;
5 – 6  - по
- по  .
. 
Зауважимо, що в результаті склеювання завжди утворюється елементарна кон’юнкція, яка є спільною частиною склеюваних конституент.
Одержали множину імплікант 2-го рангу:
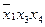 ,
, 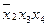 ,
,  ,
, 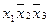 ,
, 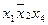 ,
, 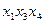 .
.
Задана перемикальна функція після склеювання приймає такий вигляд:
 .
.
1 2 3 4 5 6
Пронумеруємо ще раз одержані кон’юнкції і виконаємо ще одну операцію склеювання. В даній ДНФ можливі тільки два склеювання:
1 – 6  - по
- по  ;
;
2 – 3 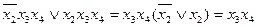 - по
- по  .
.
з утворенням однієї й тієї ж елементарної кон’юнкції 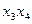 .
.
Подальше склеювання неможливе. Тоді задана перемикальна функція приймає такий вигляд
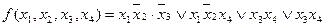 .
.
Виконавши поглинання, одержуємо скорочену ДНФ:
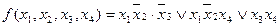 .
.
На наступному етапі мінімізації заданої перемикальної функції будуємо таблицю покриття (табл. 1. 13).
Таблиця 1. 13.
| Прості імпліканти
| Конституенти одиниці
|
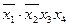
| 
| 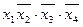
| 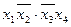
| 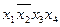
| 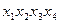
|
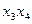
|
|
|
|
|
|
|
| +
| +
|
|
| +
| +
|

|
|
|
| +
| +
|
|
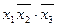
|
|
| +
| +
|
|
|
Знаходимо ядро функції – сукупність імплікант, що відповідають одноразово покритим конституентам (стовпці імплікантної матриці, що відповідають таким конституентам, мають тільки одну позначку „ + “). В даному прикладі ядро складають імпліканти 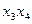 та
та 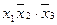 . Очевидно, що імпліканта
. Очевидно, що імпліканта  зайва, так як імпліканти
зайва, так як імпліканти 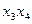 і
і 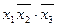 накривають всі стовпці імплікантної матриці.
накривають всі стовпці імплікантної матриці.
Задана функція  має єдину тупикову і мінімальну ДНФ
має єдину тупикову і мінімальну ДНФ
 .
.
Зауваження. Кількість  хрестиків в одному рядку завжди є степенем 2. Більш того, можна легко переконатися в тому, що
хрестиків в одному рядку завжди є степенем 2. Більш того, можна легко переконатися в тому, що  ,
,
де 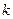 - число букв що містяться в простій імпліканті.
- число букв що містяться в простій імпліканті.
1. 6. 3. Метод мінімізації Квайна – Мак-Класкі.
Даний метод представляє собою формалізований на етапі пошуку простих імплікант метод Квайна. Суть формалізації полягає у наступному:
1. Всі конституенти одиниці із ДДНФ булевої функції  записуються їх двійковими номерами.
записуються їх двійковими номерами.
2. Всі номери розбиваються на групи, що не перетинаються. Ознакою утворення 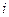 -ї групи являється наявність
-ї групи являється наявність 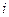 одиниць в кожному двійковому номері конституенти одиниці.
одиниць в кожному двійковому номері конституенти одиниці.


 .
. яким-небудь десятковим номером.
яким-небудь десятковим номером.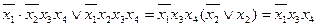 - по
- по  ;
;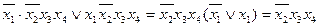 - по
- по  ;
;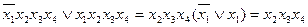 - по
- по 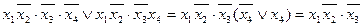 - по
- по 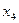 ;
;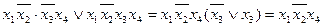 - по
- по 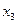 ;
; - по
- по 
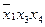 ,
, 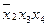 ,
,  ,
, 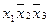 ,
, 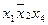 ,
, 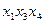 .
. .
. - по
- по 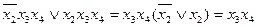 - по
- по 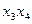 .
.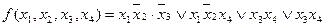 .
.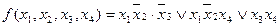 .
.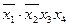

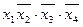
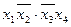
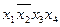
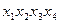

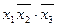
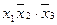 . Очевидно, що імпліканта
. Очевидно, що імпліканта  має єдину тупикову і мінімальну ДНФ
має єдину тупикову і мінімальну ДНФ .
. хрестиків в одному рядку завжди є степенем 2. Більш того, можна легко переконатися в тому, що
хрестиків в одному рядку завжди є степенем 2. Більш того, можна легко переконатися в тому, що  ,
,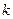 - число букв що містяться в простій імпліканті.
- число букв що містяться в простій імпліканті.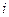 -ї групи являється наявність
-ї групи являється наявність