Procedure InputDate виконує введення даних в програму.
Procedure Vkazivka виконує вказівки для знаходження об'єму конуса. Procedure OutputDate виконує виведення даних на дисплей.
Всі змінні, які використовуються в процедурах без параметрів, описуються в основній програмі.
Задача. Скласти програму знаходження об'єму конуса.
ProgramVkonus;
Const P=3.14;
Var R,H,V:real;
procedureInputDate;
beginwrite('r=');
readln(R);
write('h=');
readln(H);
end;
procedureVkazivka;
begin
V:=P*Sqr(R)*H/3;
end;
procedureOutputDate;
begin
writeln('V=',V);
end;
begin{Основна програма}
InputDate;
Vkazivka;
OutputDate;
end.
Процедури з параметрами
У процедурі можна оголошувати константи, змінні, інші процедури і функції. Розділ опису в процедурах має таку саму структуру, як і в основній програмі.
Оголошені всередині процедури змінні називаються локальними по відношенню до даної процедури. Локальні змінні не доступні поза межами даної процедури. Зміни, які відбуваються з локальними змінними всередині процедури, не впливають на значення змінних з такими самими іменами, які описані поза даною процедурою.
Змінні, які використовуються в процедурі, але описані поза нею, називаються глобальнимипо відношенню до даної процедури. Будь-які зміни значень глобальних змінних всередині процедури змінюють значення цих змінних поза процедурою.
Приклад програми, в якій використовується принцип локалізації.
Program LOKALIZACIA;
Var A,B: integer;
procedure LOKAL;
var A,X:char;
begin
А:='!';
Х:='?';
В:=В+1;
end;
begin
А:=0;
В:=100;
LOKAL;
writeln('a=',A,' b=',B);
end.
Змінна X — локальна для процедури LOKAL, тому головна програма не може змінити її значення або звернутись до неї.
Змінна В — глобальна для процедури LOKAL, вона відома і в програмі, і в процедурі. Поскільки в процедурі немає іншого оголошення для змінної В, то всі зміни, які відбуваються зі значенням В в процедурі, зберігаються і після виходу з неї.
Змінна А в основній програмі належить до цілого типу, але в процедурі LOKAL є своя власна змінна А, яка належить до типу char. Змінна А з головної програми недоступна в процедурі LOKAL. Всі зміни, які відбуваються зі значенням А в процедурі, втрачають свій зміст при виході з неї.
Отже, в результаті виконання програми LOKAL на екран будуть виведені два числа: а=0 і b= 101.
В Турбо-Паскалі введено розширення мови, завдяки чому в процедурі можуть бути доступними як локальні відносно неї змінні, так і змінні з такими ж іменами, які описані в основній програмі. Для того, щоб реалізувати таку можливість, звернення до змінних в процедурі виконується таким чином. До локальних змінних звернення реалізується просто по їх імені (тобто як в стандартній мові). Для звернення до змінних, які однойменні з локальними, але введені в основній програмі, використовується така форма:
ім'я програми. ім'я змінної
ім'я програми — ім'я програми, яке вказано в заголовку програми "program ..."
ім'я змінної— ідентифікатор змінної, вказаний в розділі опису змінних — "var ...."
З врахуванням цього програму LOKALIZACIA можна перетворити так, щоб в процедурі LOKAL були доступні однойменні змінні, описані як в самій процедурі, так і в основній програмі.
Звернення до процедур і функцій
Program LOKALIZACIA 1;
Var A,B: integer;
procedure LOKAL;
var A,X: char;
begin
A:= '!';
X:= '?';
B:=B+1;
LOKALIZACIAl.A:=LOKALIZACIA1.A+12;
end;
begin
A:=0;
B:=100;
LOKAL;
writeln('a=‘,A,‘b=‘,b);
end.
В результаті виконання програми Lokalizacial на екрані появляться такі значення змінних: а=12 і b=101.
2. Параметри-значення і параметри-змінні у процедурах
1.Параметри-значення
Наведений вище формат опису процедури можна доповнити таким чином. Після заголовка процедури в круглих дужках можуть вказуватись змінні (з допомогою яких в процедуру передаються дані) і їх типи, які називаються параметрами-значеннями.Перед ними відсутнє службове слово VAR.
Формат запису процедури:
ім'я процедури (ім'я змінної:тип змінної);
тіло процедури;
Змінні, які описані в заголовку процедури, називаються формальними параметрами. Змінні або константи, які описані у вказівці процедури при її виклику, називаються
фактичними параметрами.
При зверненні до процедури з параметрами всі формальні параметри замінюються фактичними в порядку їх перелічення.
Program PARAMETR;
Var C,D:integer;
procedure PARAM(A,B: integer);
var S: integer;
begin
S:=0;
S:=A+B;
writeln('s=',S)
end;
begin
С:=10;
D:=100;
param(C,D); { 1-ий спосіб }
param( 10,100) { 2-ий спосіб }
end.
Змінні А і В — це формальні параметри. Змінні С і D — фактичні параметри. Значення фактичних параметрів С=10 і D=100 передаються формальним параметрам А і В.
Зверніть увагу на те, як двома способами можна викликати процедуру і передати значення змінним.
Такий спосіб передачі параметрів процедурі називається передачею за значенням. При цьому значення фактичного параметра робиться доступним для процедури. Його можна використовувати в роботі, змінювати довільним чином. Але ці зміни проявляються тільки в межах процедури, тобто є локальними. Вони не впливають на фактичні параметри поза процедурою.
2. Параметри-змінні
Для того, щоб процедура змогла змінювати значення фактичних параметрів, потрібно змінити спосіб передачі параметрів в процедуру. Новий спосіб називається передачею по імені.
При використанні цього способу заголовок процедури змінюється таким чином: перед ідентифікатором формального параметра в заголовку процедури вказується службове слово Var.
Змінні, перед якими записане службове слово Var, називаються параметрами-змінпими.
При виконанні процедури формальні параметри-змінні замінюються фактичними параметрами. Будь-які зміни значення формального параметру-змінної приводять до зміни значення фактичного параметру-змінної. За допомогою параметрів-змінних в основну програму передаються результати дії вказівок над даними.
Задача. Дано дві трійки чисел: А1, В1, СІ і А2, В2, С2.
Знайти значення сум:
S1 = min(Al, В1, СІ) + min(A2, В2, С2),
S2 = max(Al, В1, СІ) + max(А2, В2, С2).
Звернення до процедур і функцій
Для знаходження тіп і max з трьох чисел використаємо процедуру МіnМах.
Program PRIKLAD;
Var Al,Bl,Cl,A2,B2,C2,MІNl,MIN2,MAXl,MAX2,Sl,S2:real;
procedure MinMax(A,B,C:real; var MIN,MAX:real);
begin
MAX:=A;
if MAX<B then MAX:=B;
if MAX<C then MAX:=C;
MIN:=A;
if MIN>B then min:=B;
if МIN>С then MIN:=C; end;
begin
write('Al=');
readln(Al);
write('Bl=');
readln(Bl);
write('Cl=');
readln(Cl);
write('A2=');
readln(A2);
write('B2=');
readln(B2);
write('C2=');
readln(C2);
MinMax(A 1 ,B 1 ,C 1 ,MIN 1 ,MAX 1);
MinMax(A2,B2,C2,MIN2,MAX2);
S1:=MIN1+MIN2;
S2:=MAX1+MAX2;
Writeln('Sl=',Sl);
Writeln('S2=',S2);
end.
3. Функції
Якщо результатом виконання деякої процедури є одне скалярне значення, то цю процедуру бажано оформити як функцію. Формат опису функції:
function <ім'я функції>(список формальних параметрів):<тип результату>;
Звернення до функції (обов'язково повинно бути включене у вираз як операнд) має такий вигляд :
<ім'я функції> (список фактичних параметрів).
Задача. Знайти значення числа комбінацій n!
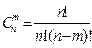
Знаходження значення факторіалу числа оформимо у вигляді функції. Тоді програма розв'язання даної задачі матиме вигляд:
Program KOMBINACIJ;
var N,M,C:integer;
function FACT(K:integer):integer;
var i,F:integer;
begin
F:=l;
for i:=l to K do F:=F*i;
FACT:=F;
end;
begin
write('n=');
readln(N);
write('m=');
readln(M);
C:=FACT(N)Div(FACT(M)*FACT(N-M));
Writeln ('Кількість комбінацій з ',n,' no ',m,' = ',C);
end.
Зверніть увагу на те, що в самому тілі функції FACT необхідно змінній, ім'я якої співпадає з ім'ям самої функції, присвоїти значення результату виконання функції: FACT:=F.
Задача 1. Знайти площу п’ятикутника, у якого сторони дорівнють:
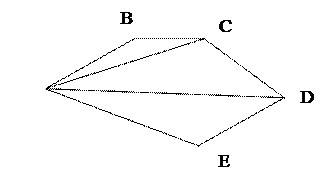 AB = 2м, BC =a м, CD = b м, DE = cм, AE = d м, AC =4 м, AD = 5 м.
AB = 2м, BC =a м, CD = b м, DE = cм, AE = d м, AC =4 м, AD = 5 м.
Program Pyatukytnuk;
Var
a,b,c,d,f,g,h: integer;
S,S1,S2,S3 : real;
Function ploscha(x,y,z:integer):real;
Var
p,S:real;
begin
If (x+y>z) and (x+z>y) and (y+z>x) Then
begin
P:=(x+y+z)/2;
S:=sqrt(p*(p-x)*(p-y)*(p-z));
end
Else
begin
Writeln(‘Такий трикутник не існує’);
S:=0
end;
ploscha:=S
End;
Begin
Write (‘Введіть сторону=BC> ‘);
ReadLn(a);
Write (‘Введіть сторону=CD> ‘);
ReadLn(b);
Write (‘Введіть сторону=DE> ‘);
ReadLn(c);
Write (‘Введіть сторону=AE> ‘);
ReadLn(d);
f:=2;
g:=4;
h:=5;
S1:=ploscha(f,a,g);
S2:=ploscha(g,b,h);
S3:=ploscha(h,c,d);
if (S1<>0) and (S2<>0) and (S3<>0) then
begin
S:=S1+S2+S3;
Writeln(‘S=’,s:5:2)
end
else
begin
Writeln(‘Пятикутника не існує’);
Writeln(‘уведіть іншу величину сторін)’;
end;
ReadLn;
End.
Задача. За допомогою функції, що визначає, яке з двох чисел більше, визначити яке з чотирьох чисел більше.
Program max_4chucla;
Uses crt;
Var
a,b,c,d,max:real;
Function maximym(a,b,max:real):real;
begin
Max:=a;
If max<b then max:=b;
Maximym:=max;
end;
Begin
clrscr;
write('a=>');
readln(a);
write('b=>');
readln(b);
write('c=>');
readln(c);
write('d=>');
readln(d);
max:=maximym(maximym(maximym(a,b,max),c,max),d,max);
writeln('max=',max:4:2);
readln;
End.
Запитання для самоконтролю:
- Для чого призначені процедури ?
- Як описується заголовок процедури ?
- Чим відрізняються формальні і фактичні параметри ?
- Чим відрізняються локальні і формальні змінні ?
- Для чого призначені функції ?
- Як описується заголовок функції ?
- Яка різниця між процедурою і функцією ?
- Як викликаються процедури і функції ?
Завдання
Знайти довжину сторін трикутника АВС, якщо відомі координати його вершин А(х1,y1,z1), B(х2,y2,z2), C(х3,y3,z3). Необхідно скористатись формулою:
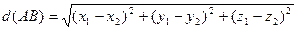
нормальні форми
Крім канонічних форм (ДДНФ і ДКНФ) існують і нормальні форми перемикальних функцій: диз’юнктивна нормальна форма (ДНФ) і кон’юнктивна нормальна форма (КНФ). Довершені нормальні форми (ДДНФ і ДКНФ) відрізняються від нормальних форм тим, що завжди містять терми тільки максимального рангу і дають однозначне представлення функції.
Довільну диз’юнктивну нормальну форму можна перетворити наступним чином.
Допустимо, що в терм  нормальної форми ДНФ перемикальної функції
нормальної форми ДНФ перемикальної функції  не входить змінна
не входить змінна 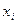 . Тоді одержати терм максимального рангу можна із виразу
. Тоді одержати терм максимального рангу можна із виразу
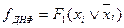 . (1. 5)
. (1. 5)
Приклад. Перемикальну функцію, задану в ДНФ
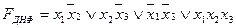 , перетворити в ДДНФ.
, перетворити в ДДНФ.
Для отримання ДДНФ заданої функції перетворимо кожний її терм згідно з виразом (1. 5).
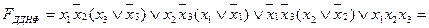
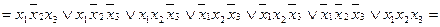
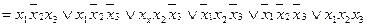 .
.
Довільна кон’юнктивна нормальна форма може бути перетворена в ДКНФ так.
Допустимо, що в диз’юнктивний терм  нормальної кон’юнктивної форми перемикальної функції
нормальної кон’юнктивної форми перемикальної функції 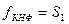 не входить змінна
не входить змінна 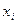 . Тоді одержати терм максимального рангу можна наступним перетворенням
. Тоді одержати терм максимального рангу можна наступним перетворенням
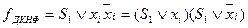 . (1. 6)
. (1. 6)
Приклад. Перетворити в ДКНФ перемикальну функцію
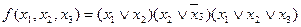 .
.
Застосувавши правило перетворення (1. 6) до першого і другого термів функції, після спрощень одержимо
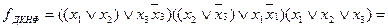
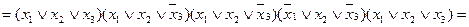
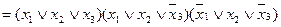 .
.
1.4.2. Алгебра Шефера
Алгебра Шефера визначена на 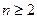 елементах і містить тільки одну функцію І-НЕ (функцію Шефера), яку для
елементах і містить тільки одну функцію І-НЕ (функцію Шефера), яку для 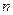 аргументів можна записати у вигляді
аргументів можна записати у вигляді
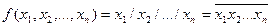 .
.
Аксіоми алгебри Шефера:
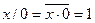 ;
; 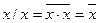 ;
;
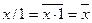 ;
;  .
.
У алгебрі Шефера виконується тільки закон (властивість) комутативності (переставний закон)
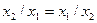 .
.
Через те, що закон асоціативності (сполучний закон) не виконується, тобто
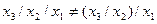 ,
,
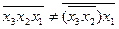 ,
,
ускладнюється порівняно із функцією І каскадування елементів для одержання функції І-НЕ з більшою кількістю аргументів на базі логічних елементів І-НЕ із кількістю входів, меншою необхідної. Наприклад, якщо елементи мають два входи , а необхідно одержати функцію трьох аргументів, то еквівалентну форму в алгебрі Шефера можна одержати так:
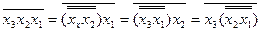 .
.
Таким чином, схема, що реалізує праву частину співвідношення, повинна мати три рівні.
Канонічна нормальна форма в алгебрі Шефера містить терми Шефера 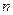 -го рангу і забезпечує дворівневу схему. Змінні в термах і самі терми об’єднуються операцією І-НЕ.
-го рангу і забезпечує дворівневу схему. Змінні в термах і самі терми об’єднуються операцією І-НЕ.
Для одержання канонічної форми виписують терми Шефера для наборів, на яких функція приймає одиничні значення. Наприклад, якщо перемикальна функція на наборах з номерами 0, 4 і 6 приймає одиничні значення, то канонічна нормальна форма в алгебрі Шефера складатиметься із термів Шефера для відповідних наборів функції і матиме такий вигляд:
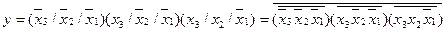 .
.
Враховуючи, що в алгебрі Шефера нема функції НЕ, заперечення над буквами означає, що змінні можуть поступати на входи логічних елементів із запереченнями. Якщо це неможливо, то у формі виконується заміна згідно з аксіомою 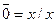 . В цьому випадку одержана нормальна форма матиме вигляд
. В цьому випадку одержана нормальна форма матиме вигляд
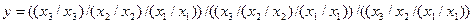 .
.
Канонічну нормальну форму в алгебрі Шефера можна також одержати із ДДНФ за допомогою правила де Моргана.
Для функції, що розглядається, можна записати

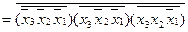 .
.
Приклад. Одержати канонічну нормальну форму алгебри Шефера для функції, що задана у ДДНФ:
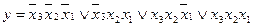 .
.
Побудувати комбінаційну схему реалізації функції на елементах І-НЕ, вважаючи, що на входи логічних елементів можуть подаватися аргументи та їх заперечення.
Застосовуючи правило де Моргана, отримаємо:
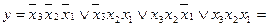
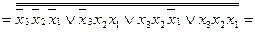

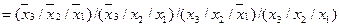 .
.
Комбінаційна схема, що реалізує задану функцію зображена на
рис. 1. 5.
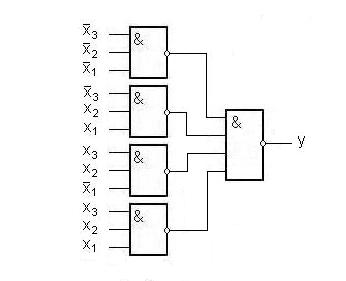
Рис. 1. 5. Схема функції  в елементному базисі алгебри Шефера
в елементному базисі алгебри Шефера
1.4.3. Алгебра Пірса
Алгебра Пірса визначена на  елементах і містить тільки одну функцію АБО-НЕ (функцію Пірса або Веба), яку для
елементах і містить тільки одну функцію АБО-НЕ (функцію Пірса або Веба), яку для  аргументів можна записати у вигляді
аргументів можна записати у вигляді
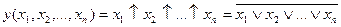 .
.
Основні аксіоми алгебри Пірса:
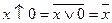 ;
;  ;
;
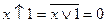 ;
; 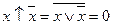 .
.
Властивості алгебри Пірса і Шефера однакові. В алгебрі Пірса, як і в алгебрі Шефера, виконується тільки закон (властивість) комутативності
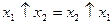 .
.
У алгебрі Пірса, як і у алгебрі Шефера, закон (властивість) асоціативності не виконується, тобто
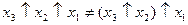 ,
,
 .
.
У наслідок цього ускладнюється порівняно із функцією АБО каскадування елементів для одержання функції АБО-НЕ із меншою від необхідної кількістю входів. Наприклад, якщо елементи мають два входи, а необхідно одержати функцію трьох аргументів, то форму у алгебрі Пірса можна одержати так:
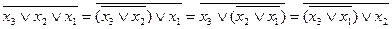 .
.
Канонічна нормальна форма в алгебрі Пірса забезпечує дворівневу комбінаційну схему і складається із термів Пірса. Змінні в термах і самі терми об’єднуються операцією АБО-НЕ.
Для одержання канонічної нормальної форми виписують терми Пірса для наборів, на яких функція приймає нульові значення. Наприклад, якщо перемикальна функція на наборах з номерами 0, 4 і 6 приймає нульові значення, то канонічна нормальна форма в алгебрі Пірса складатиметься із термів Пірса для відповідних наборів функції і матиме такий вигляд:
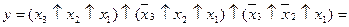
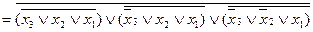 .
.
Канонічну нормальну форму в алгебрі Пірса можна також одержати із ДКНФ за допомогою правила де Моргана. Для функції, що розглядається, можна записати

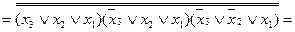
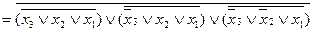 .
.
Приклад. Одержати канонічну нормальну форму алгебри Пірса для функції, що задана у ДКНФ:
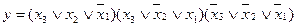 .
.
Побудувати комбінаційну схему реалізації функції на елементах АБО-НЕ з будь-якою кількістю входів за умови, що на входи логічних елементів можуть подаватися тільки прямі значення аргументів.
Із застосуванням правила де Моргана та аксіоми 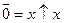 , отримаємо:
, отримаємо:

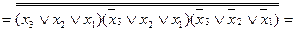
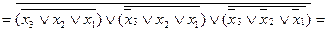

 .
.
Комбінаційна схема, що реалізує задану перемикальну функцію, зображена на рис. 1. 6.
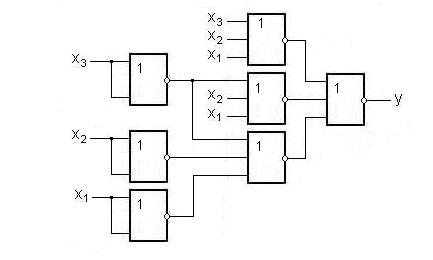
Рис. 1. 6. Схема функції 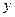 на елементах АБО-НЕ
на елементах АБО-НЕ
1.4.4. Алгебра Жегалкіна
В деяких випадках перетворення над формулами перемикальних функцій зручно здійснювати в алгебрі Жегалкіна.
Алгебра Жегалкіна включає дві двомісні операції: кон’юнкцію і додавання за модулем 2, а також константу 1, тобто система функцій алгебри Жегалкіна містить двомісні функції І та ВИКЛЮЧНЕ АБО (сума за модулем 2), а також константу 1:
 ;
;
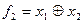 ;
;
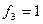 .
.
Місткість функцій І та ВИКЛЮЧНОГО АБО може бути збільшена, але за непарного числа аргументів вводиться додатково константа 0. Це пояснюється необхідністю мати в системі функцію, що не зберігає 1, для забезпечення функціональної повноти системи функцій цієї алгебри (див. параграф 1.5).
Аксіоми алгебри Жегалкіна:
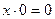 ;
; 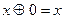 ;
;
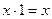 ;
; 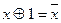 ;
;
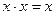 ;
; 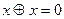 ;
;
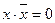 ;
;  .
.
Основні закони (властивості) алгебри Жегалкіна:


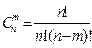
 AB = 2м, BC =a м, CD = b м, DE = cм, AE = d м, AC =4 м, AD = 5 м.
AB = 2м, BC =a м, CD = b м, DE = cм, AE = d м, AC =4 м, AD = 5 м.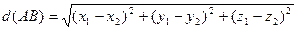
 нормальної форми ДНФ перемикальної функції
нормальної форми ДНФ перемикальної функції 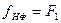 не входить змінна
не входить змінна 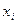 . Тоді одержати терм максимального рангу можна із виразу
. Тоді одержати терм максимального рангу можна із виразу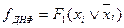 . (1. 5)
. (1. 5)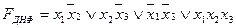 , перетворити в ДДНФ.
, перетворити в ДДНФ.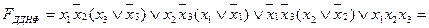
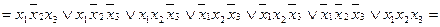
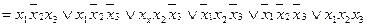 .
. нормальної кон’юнктивної форми перемикальної функції
нормальної кон’юнктивної форми перемикальної функції 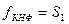 не входить змінна
не входить змінна 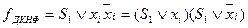 . (1. 6)
. (1. 6)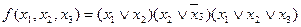 .
.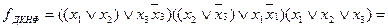
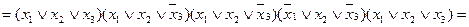
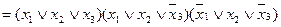 .
.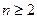 елементах і містить тільки одну функцію І-НЕ (функцію Шефера), яку для
елементах і містить тільки одну функцію І-НЕ (функцію Шефера), яку для 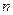 аргументів можна записати у вигляді
аргументів можна записати у вигляді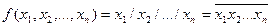 .
.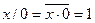 ;
; 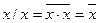 ;
;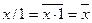 ;
;  .
.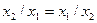 .
.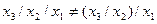 ,
,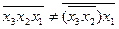 ,
,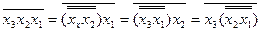 .
.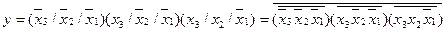 .
.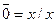 . В цьому випадку одержана нормальна форма матиме вигляд
. В цьому випадку одержана нормальна форма матиме вигляд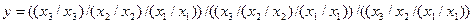 .
.
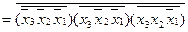 .
.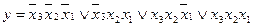 .
.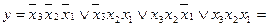
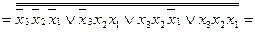

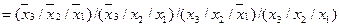 .
.
 в елементному базисі алгебри Шефера
в елементному базисі алгебри Шефера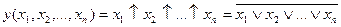 .
.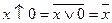 ;
;  ;
;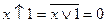 ;
; 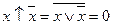 .
.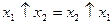 .
.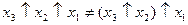 ,
, .
.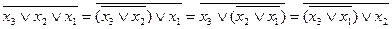 .
.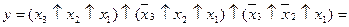
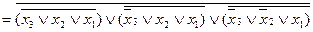 .
.
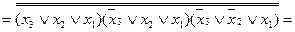
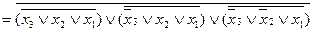 .
.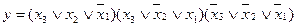 .
.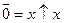 , отримаємо:
, отримаємо: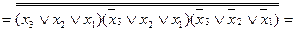
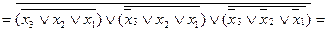

 .
.
 ;
;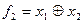 ;
;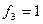 .
.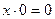 ;
; 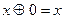 ;
;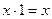 ;
; 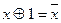 ;
;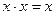 ;
; 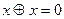 ;
;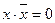 ;
;  .
.