Модель шифрування-дешифрування
Прийняті позначення
М - алфавіт джерела повідомлення, 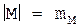 - об’єм алфавіта джерела,
- об’єм алфавіта джерела, 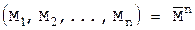 - послідовність довжини n із символів алфавіта джерела повідомлення,
- послідовність довжини n із символів алфавіта джерела повідомлення,
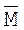 - послідовність із символів алфавіта джерела повідомлення,
- послідовність із символів алфавіта джерела повідомлення,
М - символи алфавіта джерела повідомлення,
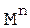 - численність усіх можливих послідовностей довжини n,
- численність усіх можливих послідовностей довжини n,
К - алфавіт ключів (ключових даних), 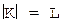 - об’єм алфавіта ключа,
- об’єм алфавіта ключа,
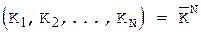 - послідовність довжини N із символів алфавіта ключа,
- послідовність довжини N із символів алфавіта ключа,
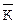 - послідовність із символів алфавіта ключа,
- послідовність із символів алфавіта ключа,
К - символ алфавіта ключа,
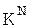 - численність усіх можливих послідовностей ключа довжиной N,
- численність усіх можливих послідовностей ключа довжиной N,
 - об’єм численності усіх можливих послідовностей ключів довжини N,
- об’єм численності усіх можливих послідовностей ключів довжини N,
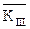 - ключова послідовність, яку використовують для шифрування,
- ключова послідовність, яку використовують для шифрування,
 - ключова послідовність, яку використовують для дешифрування,
- ключова послідовність, яку використовують для дешифрування,
Е - алфавіт джерела кріптограми, 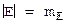 - об’єм алфавіта кріптограми,
- об’єм алфавіта кріптограми,
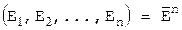 - послідовність довжини n із символів алфавіта Е,
- послідовність довжини n із символів алфавіта Е,
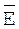 - послідовність із символів алфавіта кріптограми,
- послідовність із символів алфавіта кріптограми,
Е - символ алфавіта кріптограми,
 - численність усіх можливих послідовностей кріптограми довжиной n,
- численність усіх можливих послідовностей кріптограми довжиной n,
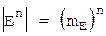 - об’єм численності усіх можливих послідовностей довжини n,
- об’єм численності усіх можливих послідовностей довжини n,
Å - додавання по модулю 2 (mod2).
Будемо далі, як правило, розглядати шифрування-дешифрування так званих діскретних повідомлень, які можуть бути представлені сигналами, які мають кінцеве число станів. Це дані, печатні тексти, а також речові сигнали та зображення, якщо вони попередньо перетворені у діскретні (цифрові) сигнали. У випадку аналогового сигнала (як правило) використовують інші методи, які будуть розглядатися далі.
Математичною моделлю системи шифрування-дешифрування називають пару функцій
 (2.1)
(2.1)
які перетворюють повідомлення 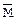 у кріптограму
у кріптограму 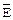 за допомогою ключа шифрування
за допомогою ключа шифрування  та навпаки, кріптограму
та навпаки, кріптограму 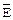 у повідомлення
у повідомлення 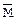 за допомогою ключа дешифрування
за допомогою ключа дешифрування  . Обидві функції, які задають кріптосистему, повинні задовольнити таким вимогам:
. Обидві функції, які задають кріптосистему, повинні задовольнити таким вимогам:
1. функція f(,) та g(,)при відомих аргементах розраховуються просто.
2. функція g(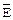 ,?) при невідомому ключі
,?) при невідомому ключі  розраховується складно.
розраховується складно.
Передбачається, що ключ дешифрування 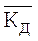 невідомий нелегальним користувачам, хоч вони і можуть знати функції f(,) та g(,), а також ключ шифрування
невідомий нелегальним користувачам, хоч вони і можуть знати функції f(,) та g(,), а також ключ шифрування 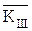 . (Остання умова складає так званий принцип Казиски).
. (Остання умова складає так званий принцип Казиски).
Слід розрізняти три основних вида нападу (атаки) опонентів на кріптограму:
1. Напад при відомій кріптограмі 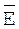 .
.
2. Напад при відомій частині кріптограми 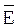 та повідомлення
та повідомлення 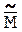 , яка відповідає певній частині криптограми, яку отримали при використанні того ж самого ключа (атака при частково відомому відкритому повідомлені).
, яка відповідає певній частині криптограми, яку отримали при використанні того ж самого ключа (атака при частково відомому відкритому повідомлені).
3. Напад при відомій криптограмі та спеціально вибраній частині повідомлення, яка відповідає цій частині кріптограми, яку отримали на тому ж ключі (атака з частково вибраними відкритими повідомленнями).
Сучасні кріптосистеми важаються стійкими, якщо вони стійки до всіх трьох атак.
Для кріптосистем, які шифрують повідомлення з невисокими вимогами до ймовірності помилки при передачі (цифрова реч, цифрове зображення), необхідно дати четверту, додаткову вимогу.
4. Дешифрування після передачі кріптограми по каналам зі спотвореннями не повинно збільшувати число помилок у порівнянні з тим числом помилок, які виникли у каналі зв’язку внаслідок спотворень, іншими словами не повинно відбуватися розмноження помилок.
Пояснемо суть поняття розмноження помилок. Нехай при передачі кріптограми  по каналу зв’язку виникли помилки (див. мал. 2.1).
по каналу зв’язку виникли помилки (див. мал. 2.1).
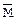
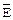
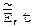
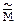 ,t
,t



Мал. 2.1. Система шифрування-дешифрування
Місцезнаходження та величина помилок виначаються вектором помилок 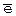 . При двоїчній системі передачі прийнята криптограма буде мати вигляд
. При двоїчній системі передачі прийнята криптограма буде мати вигляд 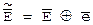 , де знак Å означає побітне додавання по модуля два, а загальне число помилок t дорвінює нормі векторів помилок
, де знак Å означає побітне додавання по модуля два, а загальне число помилок t дорвінює нормі векторів помилок 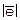 , тобто t=
, тобто t=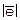 . Число помилок t’ у розшифрованому повідомлені
. Число помилок t’ у розшифрованому повідомлені 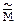 підраховується як
підраховується як
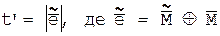 (2.2)
(2.2)
Помилки не розмножуються при умові, що t’=t.
Якщо ключ шифрування дорівнює ключу дешифрування, тобто
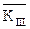 =
=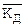 =
=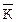 , (2.3)
, (2.3)
то система називається сіметрічною (одноключовою). Тоді у пункти шифрування та дешифрування повинні бути доставлені однакові ключі. Якщо  ¹
¹ , то система шифрування називається несіметрічною (двоключовою). У цьому випадку ключ
, то система шифрування називається несіметрічною (двоключовою). У цьому випадку ключ  доставляється у пункт шифрування, а
доставляється у пункт шифрування, а  - у пункт дешифрування. Оба ключа повинні бути зв’язані функціональною залежністю
- у пункт дешифрування. Оба ключа повинні бути зв’язані функціональною залежністю  =j(
=j( ), але такою, щоб відомому ключу шифрування неможливо було б відтворити ключ дешифрування. Для несіметрічних систем шифрування j() повинна бути складно розрахуємою функцією. У такій системі є можливість секретним чином розподіляти серед законних користувачів тільки їх ключі дешифрування, а ключі шифрування зробити відкритими та оприлюднити, наприклад у загальнодоступному довіднику. Розглядаєма система тому називається системою з відкритим (загальнодоступним) ключом
), але такою, щоб відомому ключу шифрування неможливо було б відтворити ключ дешифрування. Для несіметрічних систем шифрування j() повинна бути складно розрахуємою функцією. У такій системі є можливість секретним чином розподіляти серед законних користувачів тільки їх ключі дешифрування, а ключі шифрування зробити відкритими та оприлюднити, наприклад у загальнодоступному довіднику. Розглядаєма система тому називається системою з відкритим (загальнодоступним) ключом  . Кріптосистема з загальнодоступним ключом (Public key criptosystem) була вперше запропанована Діффі та Хелманом у 1978р.
. Кріптосистема з загальнодоступним ключом (Public key criptosystem) була вперше запропанована Діффі та Хелманом у 1978р.
У цій частині курсу будуть розглядатися тільки одноключові системи.


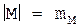 - об’єм алфавіта джерела,
- об’єм алфавіта джерела, 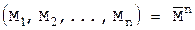 - послідовність довжини n із символів алфавіта джерела повідомлення,
- послідовність довжини n із символів алфавіта джерела повідомлення,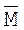 - послідовність із символів алфавіта джерела повідомлення,
- послідовність із символів алфавіта джерела повідомлення,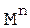 - численність усіх можливих послідовностей довжини n,
- численність усіх можливих послідовностей довжини n,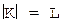 - об’єм алфавіта ключа,
- об’єм алфавіта ключа,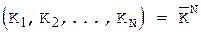 - послідовність довжини N із символів алфавіта ключа,
- послідовність довжини N із символів алфавіта ключа,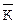 - послідовність із символів алфавіта ключа,
- послідовність із символів алфавіта ключа,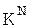 - численність усіх можливих послідовностей ключа довжиной N,
- численність усіх можливих послідовностей ключа довжиной N, - об’єм численності усіх можливих послідовностей ключів довжини N,
- об’єм численності усіх можливих послідовностей ключів довжини N,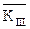 - ключова послідовність, яку використовують для шифрування,
- ключова послідовність, яку використовують для шифрування, - ключова послідовність, яку використовують для дешифрування,
- ключова послідовність, яку використовують для дешифрування,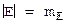 - об’єм алфавіта кріптограми,
- об’єм алфавіта кріптограми,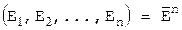 - послідовність довжини n із символів алфавіта Е,
- послідовність довжини n із символів алфавіта Е,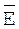 - послідовність із символів алфавіта кріптограми,
- послідовність із символів алфавіта кріптограми, - численність усіх можливих послідовностей кріптограми довжиной n,
- численність усіх можливих послідовностей кріптограми довжиной n,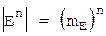 - об’єм численності усіх можливих послідовностей довжини n,
- об’єм численності усіх можливих послідовностей довжини n, (2.1)
(2.1)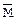 у кріптограму
у кріптограму 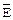 за допомогою ключа шифрування
за допомогою ключа шифрування  та навпаки, кріптограму
та навпаки, кріптограму 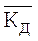 невідомий нелегальним користувачам, хоч вони і можуть знати функції f(,) та g(,), а також ключ шифрування
невідомий нелегальним користувачам, хоч вони і можуть знати функції f(,) та g(,), а також ключ шифрування 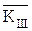 . (Остання умова складає так званий принцип Казиски).
. (Остання умова складає так званий принцип Казиски).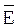 та повідомлення
та повідомлення 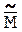 , яка відповідає певній частині криптограми, яку отримали при використанні того ж самого ключа (атака при частково відомому відкритому повідомлені).
, яка відповідає певній частині криптограми, яку отримали при використанні того ж самого ключа (атака при частково відомому відкритому повідомлені). по каналу зв’язку виникли помилки (див. мал. 2.1).
по каналу зв’язку виникли помилки (див. мал. 2.1).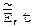
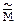 ,t
,t
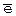 . При двоїчній системі передачі прийнята криптограма буде мати вигляд
. При двоїчній системі передачі прийнята криптограма буде мати вигляд 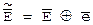 , де знак Å означає побітне додавання по модуля два, а загальне число помилок t дорвінює нормі векторів помилок
, де знак Å означає побітне додавання по модуля два, а загальне число помилок t дорвінює нормі векторів помилок 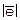 , тобто t=
, тобто t=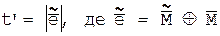 (2.2)
(2.2)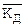 =
=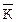 , (2.3)
, (2.3)