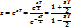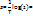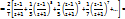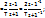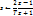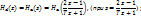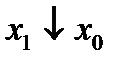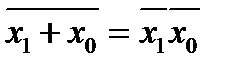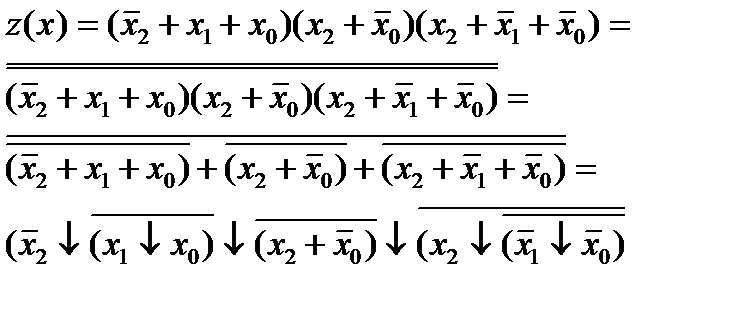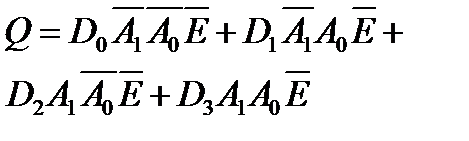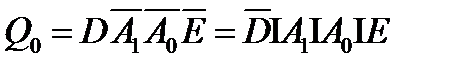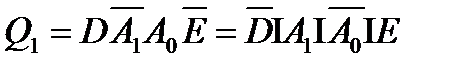Реальные сигналы могут быть описаны выборками как в спектральной, так и во временной области. Дискретный спектр, и дискретный сигнал полностью описывают исходный непрерывный сигнал. Непосредственный переход от дискретного сигнала к дискретному спектру и наоборот возможен с использованием дискретного преобразования Фурье. оно не всегда точно описывает спектр исходного непрерывного сигнала, подобно тому, как дискретизированный сигнал не всегда точно описывает исходный непрерывный сигнал. Связь между дискретным сигналом и его дискретным преобразованием Фурье всегда носит взаимно однозначный характер и формулы прямого и обратного преобразований Фурье являются строгими при любом числе дискретных значений. Формулу дискретного преобразования Фурье записывают в виде
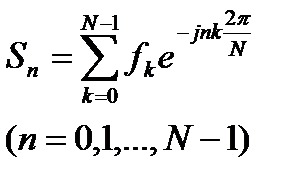 (1)
(1)
 При этом обратное дискретное преобразование Фурье имеет вид
При этом обратное дискретное преобразование Фурье имеет вид  Для определения выборочных значений Sf(nQ) надо значения Sn, умножить на величину интервала дискретизации по времени Т:
Для определения выборочных значений Sf(nQ) надо значения Sn, умножить на величину интервала дискретизации по времени Т:  преобразования являются взаимно обратными. При последовательном применении к любой числовой последовательности прямого и обратного дискретного преобразования Фурье получают в результате ту же последовательность. Одно из основных применений дискретного преобразования Фурье - это вычисление спектров функций, заданных графически или таблично. Преобразование Фурье можно применять при обработке экспериментальных данных когда надо найти энергетический спектр по корреляционной функции сигнала. Другое важное применение дискретного преобразования Фурье — вычисление сигнала на выходе фильтра с заданной частотной характеристикой. если задан входной сигнал
преобразования являются взаимно обратными. При последовательном применении к любой числовой последовательности прямого и обратного дискретного преобразования Фурье получают в результате ту же последовательность. Одно из основных применений дискретного преобразования Фурье - это вычисление спектров функций, заданных графически или таблично. Преобразование Фурье можно применять при обработке экспериментальных данных когда надо найти энергетический спектр по корреляционной функции сигнала. Другое важное применение дискретного преобразования Фурье — вычисление сигнала на выходе фильтра с заданной частотной характеристикой. если задан входной сигнал  , то для него можно вычислить дискретное преобразование Фурье
, то для него можно вычислить дискретное преобразование Фурье  . Если теперь умножим Si(nQ) на частотную характеристику фильтра, то получим дискретное преобразование Фурье выходного сигнала:
. Если теперь умножим Si(nQ) на частотную характеристику фильтра, то получим дискретное преобразование Фурье выходного сигнала:  . После этого с помощью обратного дискретного преобразования Фурье можно найти сигнал на выходе фильтра. Для повышения точности обработки сигнала обрабатываемые серии отсчетов могут частично перекрываться. Обработку сигналов с помощью дискретного преобразования Фурье нельзя назвать цифровой фильтрацией. Обычные цифровые фильтры, работающие в реальном масштабе времени, производят обработку сигнала непрерывно по мере его поступления, а вычисление выходного сигнала с помощью дискретного преобразования Фурье может быть произведено лишь после того, как станет известным полностью входной сигнал или хотя бы первая серия из N его отсчетов. Поэтому при использовании дискретного преобразования Фурье выходной сигнал может быть получен только с некоторым запаздыванием по отношению к входному сигналу. В ряде практических применений такое запаздывание выходного сигнала не играет существенной роли, и тогда обработка сигналов с использованием дискретного преобразования Фурье оказывается целесообразной.
. После этого с помощью обратного дискретного преобразования Фурье можно найти сигнал на выходе фильтра. Для повышения точности обработки сигнала обрабатываемые серии отсчетов могут частично перекрываться. Обработку сигналов с помощью дискретного преобразования Фурье нельзя назвать цифровой фильтрацией. Обычные цифровые фильтры, работающие в реальном масштабе времени, производят обработку сигнала непрерывно по мере его поступления, а вычисление выходного сигнала с помощью дискретного преобразования Фурье может быть произведено лишь после того, как станет известным полностью входной сигнал или хотя бы первая серия из N его отсчетов. Поэтому при использовании дискретного преобразования Фурье выходной сигнал может быть получен только с некоторым запаздыванием по отношению к входному сигналу. В ряде практических применений такое запаздывание выходного сигнала не играет существенной роли, и тогда обработка сигналов с использованием дискретного преобразования Фурье оказывается целесообразной.
7.19. Алгоритми швидкого перетворення Фур’є.
Одно из основных применений дискретного преобразования Фурье — это вычисление спектров функций, заданных графически или таблично. Дискретное преобразование Фурье можно применять при обработке экспериментальных данных, например в тех случаях, когда надо найти энергетический спектр по корреляционной функции сигнала.
Другое важное применение дискретного преобразования Фурье— вычисление сигнала на выходе фильтра с заданной частотной характеристикой.
Если входной сигнал имеет большую длительность, его обработку с помощью дискретного преобразования Фурье можно производить по частям. Для этого берут первые N отсчетов входного сигнала, вычисляют их дискретное преобразование Фурье и после умножения на частотную характеристику фильтра с помощью обратного дискретного преобразования Фурье вычисляют первые N отсчетов выходного сигнала. После этого аналогичным путем обрабатывают следующие N отсчетов входного сигнала и т. д. Для повышения точности обработки сигнала обрабатываемые серии отсчетов могут частично перекрываться.
Преимуществом такого метода обработки сигналов является отсутствие каких-либо ограничений на вид частотной характеристики фильтра.
Быстрое преобразование Фурье
Недостатком дискретного преобразования Фурье является большое количество математических операций. Если число степеней свободы сигнала равно N, то для расчета по формулам дискретного преобразования Фурье необходимо выполнить N* умножений и N* сложений комплексных чисел — всего 2Nг арифметических операций.
Для облегчения вычисления дискретного преобразования Фурье применяют специальные алгоритмы, которые позволяют во много раз сократить объем необходимых вычислений. Такие алгоритмы называют быстрым преобразованием Фурье.
Существует несколько различных алгоритмов быстрого преобразования Фурье. Каждый из них применяют в определенной ситуации, в зависимости оттого, на какие множители может быть разложено число степеней свободы N. Наиболее простые алгоритмы получаются, если N является степенью числа 2.
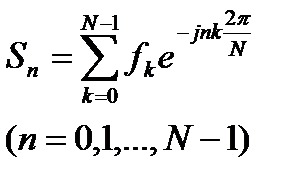
Вид формулы дискретного преобразованя Фурье.
7.22 Методи синтезу цифрових фільтрів з нескінченною імпульсною характеристикою. Метод білінійного Z-перетворення.
Билинейное преобразование представляет собой функцию, аппроксимирующую натуральный логарифм, который является точным отображением z-плоскости на s-плоскость. При взятии преобразования Лапласа над дискретным сигналом (представляющего последовательность отсчётов), результатом является Z-преобразование с точностью до замены переменных:
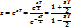
где T — период квантования (обратная к частоте дискретизации величина). Аппроксимация, приведённая выше и является билинейным преобразованием.
Обратное преобразование из s-плоскости в z-плоскость и его билинейная аппроксимация записываются следующим образом:
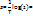
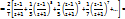
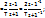
Билинейное преобразование использует это соотношения для замены передаточной функции Ha(s) на её дискретный аналог:
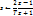
то есть:
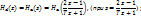
7.23 Методи синтезу цифрових фільтрів з кінцевою імпульсною характеристикою.
Фильтры с конечной импульсной характеристикой реализуются, как правило, по нерекурсивной схеме и обладают рядом положительных качеств, основное из которых состоит в том, что благодаря отсутствию обратных связей КИХ-фильтры всегда устойчивы. ; Фильтры с конечной импульсной характеристикой не имеют непосредственных аналогов среди пассивных электрических фильтров, поэтому методы их синтеза относятся к прямым методам. Одним из наиболее употребительных методов синтеза КИХ-фильтров является метод частотной в ы б о р к и.
Идея метода очень проста. Частотную характеристику цифрового фильтра подвергают дискретизации как периодическую функцию, разбивая интервал (—π/Т<ω< π/Т) , на N равных частей. Интервал дискретизации Ω должен быть таким, чтобы передать характерные подробности частотной характеристики. К образовавшейся последовательности значений К(nΩ) применяют дискретное преобразование Фурье или быстрое преобразование Фурье и ' находят импульсную характеристику g(kT).' Значения g(kT) являются коэффициентами нерекурсивного фильтра. Иногда получающаяся в процессе синтеза импульсная характеристика цифрового фильтра оказывается физически нереализуемой, так как отличны от нуля ее значения g(kT) при отрицательных kТ. Фильтр можно сделать физически реализуемым, если его импульсную характеристику сместить вправо так, чтобы для моментов времени kT<0 она тождественно равнялась нулю. При таком смещении изменяется фазочастотная характеристика цифрового фильтра, а его амплитудно-частотная характеристика остается неизменной. Поэтому метод частотной выборки позволяет синтезировать фильтры с заданной амплитудночастотной характеристикой при неконтролируемой фазочастотной характеристике.
Метод частотной выборки хорошо работает при плавных частотных характеристиках.
7.12 Комбинационные логические устройства. Типовые функциональные узлы цифровых комбинационных логических устройств.
При построении лог. устр-в обычно не пользуются функциональноно полной системой лог. элементов («и», «или», «не»), а пользуются, например, ф-но полной системой элементов включающей «и-не» (или/и «или-не»)число входов этих элементов задаётся.
Поэтому вопрос синтеза ЛУ в заданом базисе имеет большое практическое значение.



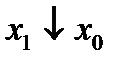

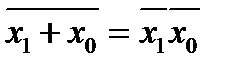
Если требуется привести ФАЛ к базису лог-го элемента «и-не» , то ф-я преобразуется к виду содержащему только операции лог. умножения и инверсии. Далее переписываем через условные обозначения операции «и-не». Аналогично поступают с ФАЛ при приведении к базису от элемента «или-не»
Особенности построения лог. устройств на реальной элементной базе:
Например 1-е: число вх. лог. элемента м. б. больше или меньше числа переменных. Приемы решения этих противо-речий: 1-е число вх. ЛЭ > числа переменных. Тут можно исполь-зовать понятия активного и пас-сивного лог. уровней, а именно при подачи на лишние входы пассивных лог. уровней результат никак не изменится.
Второй способ – это способ базирущийся на теоремах алгебры логики:
 ,
, 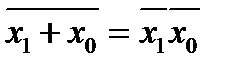 При подаче на несколько входов одной и той-же переменной результат не изменится.
При подаче на несколько входов одной и той-же переменной результат не изменится.
Например 2-е: Число вх. лог. Элемента < требуемого числа.
Активные и пассивные логические уровни.
Активным лог. уровнем называют такое значение вх переменной, кото-рое однозначно определяет выход-ной сигнал лог. элемента.
Для определения акт. лог. уровней элементов «и», «или», «и-не» и «или-не» нарисуем таблицу истинности для этих элементов:
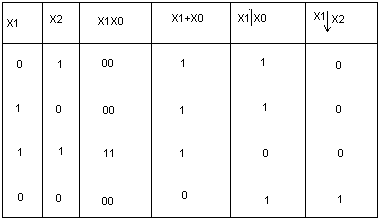
Из табл видно, что для «и-не» акт. лог. уровнем явл. сигнал лог. «0». т.к. наличие этого сигнала хотябы на одном из входов этого элемента однозначно определяет вых. «1». Сигнал лог. «1» для этого элемента определяется как пассивный.
Преобразовать ФАЛ к базису «2ИЛИ-НЕ»
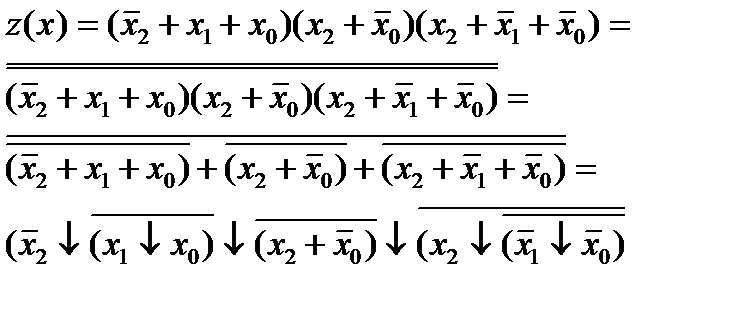
Типовые функциональные узлы комбинационных лог. устройств.
Мультиплексоры.
Мультиплексором называется комбинационное лог. устройство, предназначенное для управляемой передачи данных от нескольких источников информации в один выходной канал.
Мультиплексор осуществляет подключение различных источников инф-и к одному приёмнику по заданной команде т.е. информация разделённая в пространстве преобразуется к виду с разделением по времени.
Схема имеет один выход и две группы входов: информационные и адресные. Код на адресном входе определяет какой из инфо входов в данный момент подключён к выходу. Если число адресных входов n, то число инфо 2n . Также часто имеется ещё и разрешающий вход.
Запишем ФАЛ данного устройства и реализуем его. 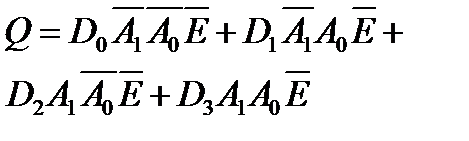
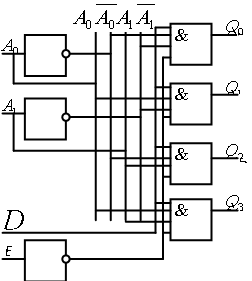
В соответствии с ФАЛ стр-ра лог. устр-ва имеет следующий вид:
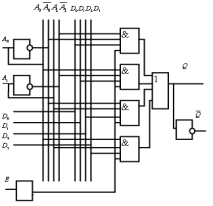
Демультиплексор – комбинационное логическое уср-во предназначенное для управляемой передачи данных от одного источника информации в несколько выходных каналов.
Имеют один инф. вход, n адресных входов и 2n выходов.
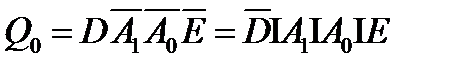
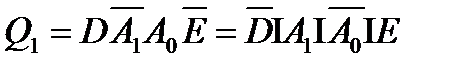


Условное графическое обозначение:
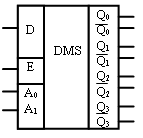
При необходимости увеличения числа выходов можно построить структуру демультиплексорного дерева.



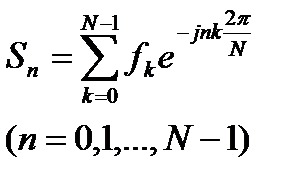 (1)
(1) Для определения выборочных значений Sf(nQ) надо значения Sn, умножить на величину интервала дискретизации по времени Т:
Для определения выборочных значений Sf(nQ) надо значения Sn, умножить на величину интервала дискретизации по времени Т:  преобразования являются взаимно обратными. При последовательном применении к любой числовой последовательности прямого и обратного дискретного преобразования Фурье получают в результате ту же последовательность. Одно из основных применений дискретного преобразования Фурье - это вычисление спектров функций, заданных графически или таблично. Преобразование Фурье можно применять при обработке экспериментальных данных когда надо найти энергетический спектр по корреляционной функции сигнала. Другое важное применение дискретного преобразования Фурье — вычисление сигнала на выходе фильтра с заданной частотной характеристикой. если задан входной сигнал
преобразования являются взаимно обратными. При последовательном применении к любой числовой последовательности прямого и обратного дискретного преобразования Фурье получают в результате ту же последовательность. Одно из основных применений дискретного преобразования Фурье - это вычисление спектров функций, заданных графически или таблично. Преобразование Фурье можно применять при обработке экспериментальных данных когда надо найти энергетический спектр по корреляционной функции сигнала. Другое важное применение дискретного преобразования Фурье — вычисление сигнала на выходе фильтра с заданной частотной характеристикой. если задан входной сигнал  , то для него можно вычислить дискретное преобразование Фурье
, то для него можно вычислить дискретное преобразование Фурье  . Если теперь умножим Si(nQ) на частотную характеристику фильтра, то получим дискретное преобразование Фурье выходного сигнала:
. Если теперь умножим Si(nQ) на частотную характеристику фильтра, то получим дискретное преобразование Фурье выходного сигнала:  . После этого с помощью обратного дискретного преобразования Фурье можно найти сигнал на выходе фильтра. Для повышения точности обработки сигнала обрабатываемые серии отсчетов могут частично перекрываться. Обработку сигналов с помощью дискретного преобразования Фурье нельзя назвать цифровой фильтрацией. Обычные цифровые фильтры, работающие в реальном масштабе времени, производят обработку сигнала непрерывно по мере его поступления, а вычисление выходного сигнала с помощью дискретного преобразования Фурье может быть произведено лишь после того, как станет известным полностью входной сигнал или хотя бы первая серия из N его отсчетов. Поэтому при использовании дискретного преобразования Фурье выходной сигнал может быть получен только с некоторым запаздыванием по отношению к входному сигналу. В ряде практических применений такое запаздывание выходного сигнала не играет существенной роли, и тогда обработка сигналов с использованием дискретного преобразования Фурье оказывается целесообразной.
. После этого с помощью обратного дискретного преобразования Фурье можно найти сигнал на выходе фильтра. Для повышения точности обработки сигнала обрабатываемые серии отсчетов могут частично перекрываться. Обработку сигналов с помощью дискретного преобразования Фурье нельзя назвать цифровой фильтрацией. Обычные цифровые фильтры, работающие в реальном масштабе времени, производят обработку сигнала непрерывно по мере его поступления, а вычисление выходного сигнала с помощью дискретного преобразования Фурье может быть произведено лишь после того, как станет известным полностью входной сигнал или хотя бы первая серия из N его отсчетов. Поэтому при использовании дискретного преобразования Фурье выходной сигнал может быть получен только с некоторым запаздыванием по отношению к входному сигналу. В ряде практических применений такое запаздывание выходного сигнала не играет существенной роли, и тогда обработка сигналов с использованием дискретного преобразования Фурье оказывается целесообразной.