3. Подаємо перелік управлінських рішень  для кожного кроку і відповідні обмеження щодо них.
для кожного кроку і відповідні обмеження щодо них.
4. Визначаємо ефект, що його забезпечує управлінське рішення 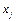 , на j- му кроці, якщо перед тим система була у стані S, як функцію ефективності:
, на j- му кроці, якщо перед тим система була у стані S, як функцію ефективності:
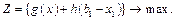
5. Досліджуємо, як змінюється стан S системи під впливом управлінського 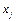 на j- му кроці, переходячи до нового стану:
на j- му кроці, переходячи до нового стану:
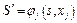 .
.
6. Будуємо для розглядуваної задачі рекурентну залежність, що визначає умовний оптимальний ефект 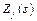 , починаючи з j- го кроку і до останнього, через вже відому функцію
, починаючи з j- го кроку і до останнього, через вже відому функцію 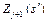 :
:
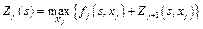
Цьому ефекту відповідає умовне оптимальне управління на j- му кроці  . Зауважимо, що за аргумент функції
. Зауважимо, що за аргумент функції 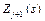 беремо не s, а змінений стан системи, тобто
беремо не s, а змінений стан системи, тобто 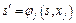 .
.
7.Здійснюємо умовну оптимізацію останнього n-го кроку, розглядаючи множину станів s, що на один крок віддалені від кінцевого стану, і визначаємо умовний оптимальний ефект на n-му кроці:
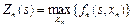
Далі знаходимо умовне оптимальне управлінське рішення 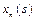 , завдяки якому цей максимум досягається.
, завдяки якому цей максимум досягається.
8. Виконуємо умовну оптимізацію 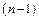 - го,
- го, 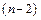 - го і т. д., тобто всіх попередніх кроків за рекурентними залежностями п.6, і для кожного кроку знаходимо умовне оптимальне управління:
- го і т. д., тобто всіх попередніх кроків за рекурентними залежностями п.6, і для кожного кроку знаходимо умовне оптимальне управління:
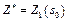
9. Здійснюємо безумовну оптимізацію управління у «зворотному» напрямі — від початкового стану 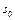 до кінцевого. Для цього з урахуванням визначеного оптимального управління на першому кроці
до кінцевого. Для цього з урахуванням визначеного оптимального управління на першому кроці 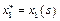 змінюємо стан системи згідно з п. 5. Далі для цього нового стану знаходимо оптимальне управління на другому кроці
змінюємо стан системи згідно з п. 5. Далі для цього нового стану знаходимо оптимальне управління на другому кроці 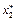 і діємо так до останнього кроку.
і діємо так до останнього кроку.
9.3. Метод рекурентних співвідношень. Використання принципу Беллмана і алгоритму Джонсона.
Фірма планує нарощувати виробничі потужності на чотирьох підприємствах, маючи для цього 4 млн грн. Для кожного з підприємств розроблено інвестиційні проекти, які відбивають прогнозовані сумарні витрати С та доходи D, пов'язані з реалізацією кожного проекту. Зміст цих проектів ілюструє таблиця:
Перший проект передбачає відмовитися від розширення підприємства, а тому має нульові витрати і доходи. Розробити план І інвестування виділених коштів у зазначені підприємства так, щоб одержати максимальний прибуток.
Розв'язування. Спрощеним і найменш ефективним способом розв'язування таких задач є перебір усіх можливих варіантів. Проте на практиці їх так багато, що проаналізувати всі і вибрати серед них найефективніший неможливо. Головними недоліками такого способу розв'язування є великий обсяг обчислень, відсутність апріорної інформації про неприпустимі розв'язки, а також немо жливість скористатися проміжними результатами аналізу для відкидання неоптимальних комбінацій проектів.
Розв'яжемо цю задачу за алгоритмом (методом) зворотного прогону. Кроками задачі вважатимемо кожне з чотирьох підпри ємств, оскільки для кожного з них маємо вибрати оптимальний інвестиційний проект за обмежених грошових ресурсів.
Зауважимо, що в цьому разі нединамічний процес розглядаємо як динамічний, аби скористатися методами динамічного програ мування для знаходження оптимального розв'язку. Зв'язок між зазначеними кроками забезпечується обмеженнями на загальний обсяг виділених коштів — 4 млн грн.
Змінні задачі візьмемо так, щоб послідовно керувати процесом розподілу коштів:
 — обсяг капіталовкладень, виділених на кроках 1—4;
— обсяг капіталовкладень, виділених на кроках 1—4;
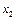 — те саме на кроках 2—4;
— те саме на кроках 2—4;
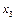 — те саме на кроках 3 і 4;
— те саме на кроках 3 і 4;
 — те саме на кроці 4.
— те саме на кроці 4.
 — обсяги інвестицій на г'-му підприємстві
— обсяги інвестицій на г'-му підприємстві  .
.
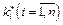 — оптимальні обсяги інвестицій на і- му підприємстві.
— оптимальні обсяги інвестицій на і- му підприємстві.
Рекурентне співвідношення для зворотного прогону від кроку 4-го до 1-го (від четвертого підприємства до першого) подається у вигляді:
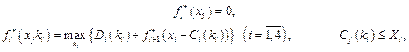
де 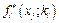 — сумарна ефективність інвестицій з і- го кроку до останнього.
— сумарна ефективність інвестицій з і- го кроку до останнього.
Тут  , оскільки п'ятого підприємства не існує. Виконаємо поетапні розрахунки за цією моделлю.
, оскільки п'ятого підприємства не існує. Виконаємо поетапні розрахунки за цією моделлю.
Етап 4.
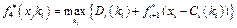
Результати розрахунків подамо табицею:

| Дохід 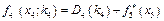
| Оптимальний розв’язок
|
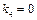
| 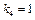
| 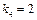
| 
| 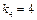
| 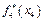
| 
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Етап 3.
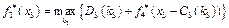
за умов

Результати розрахунків відбиває таблиця:
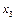
| Дохід 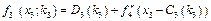
| Оптимальний розв’язок
|
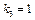
| 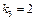
| 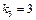
| 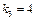
| 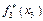
| 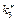
|
|
| 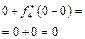
|
|
|
|
|
|
|
| 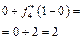
|
|
|
|
|
|
|
| 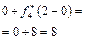
| 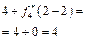
|
|
|
|
|
|
| 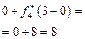
| 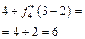
| 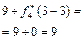
|
|
|
|
|
| 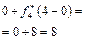
| 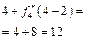
| 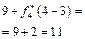
| 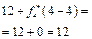
|
| 2 або 4
|
| | | | | | | | |
Розрахунки виконуються так. Нехай потрібно знайти 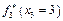 .
.
Обчислюємо
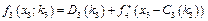 .
.
Отже,
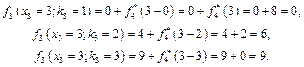
Запишемо, що 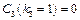 , оскільки для третього підприємства не існує проекту з інвестиціями в 1 млн грн. Значення
, оскільки для третього підприємства не існує проекту з інвестиціями в 1 млн грн. Значення 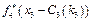 беремо з попередньої таблиці. Далі маємо:
беремо з попередньої таблиці. Далі маємо:
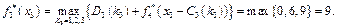
Етап 2.
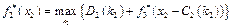
за умов

Результати розрахунків подаємо таблицею:
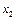
| Дохід 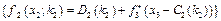
| Оптимальний розв’язок
|
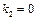
| 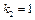
| 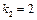
| 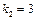
| 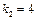
| 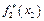
| 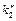
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Етап 1.
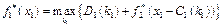
за умов

Виконуємо розрахунки лише для  , подаючи їх у вигляді таблиці:
, подаючи їх у вигляді таблиці:

| Дохід 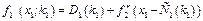
| Оптимальний розв’язок
|
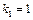
| 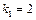
| 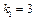
| 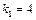
| 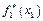
| 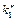
|
|
| 
| 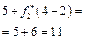
| 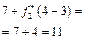
|
|
|
|
Знайдемо оптимальний план. Із таблиці першого кроку випливає, що  , тобто для першого підприємства реалізується другий проект, який використовує 1 млн грн. інвестицій з ефективністю 3 млн грн. Отже,
, тобто для першого підприємства реалізується другий проект, який використовує 1 млн грн. інвестицій з ефективністю 3 млн грн. Отже, 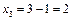 для другого, третього і четвертого підприємств залишається 4-1=3 млн грн. інвестицій. Із таблиці другого кроку маємо, що за умов
для другого, третього і четвертого підприємств залишається 4-1=3 млн грн. інвестицій. Із таблиці другого кроку маємо, що за умов 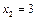 максимальний ефект настає в разі реалізації для другого підприємства першого проекту
максимальний ефект настає в разі реалізації для другого підприємства першого проекту 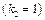 ефективність становить 4 млн грн. Отже,
ефективність становить 4 млн грн. Отже, 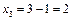 , тобто для третього і чет вертого підприємств слід використати 2 млн грн. інвестицій. Із таблиці третього кроку за умов
, тобто для третього і чет вертого підприємств слід використати 2 млн грн. інвестицій. Із таблиці третього кроку за умов 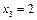 маємо, що
маємо, що 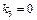 . Отже,
. Отже, 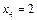 , а йому відповідають капітальні вкладення
, а йому відповідають капітальні вкладення 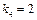 , ефективність яких 8 млн грн. Остаточно маємо: ефективність 4 млн грн. інвестицій становить 3+4 + 8=15 (млн грн.).
, ефективність яких 8 млн грн. Остаточно маємо: ефективність 4 млн грн. інвестицій становить 3+4 + 8=15 (млн грн.).
Від'ємні обернені зв'язки.


 для кожного кроку і відповідні обмеження щодо них.
для кожного кроку і відповідні обмеження щодо них.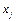 , на j- му кроці, якщо перед тим система була у стані S, як функцію ефективності:
, на j- му кроці, якщо перед тим система була у стані S, як функцію ефективності: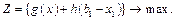
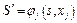 .
.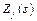 , починаючи з j- го кроку і до останнього, через вже відому функцію
, починаючи з j- го кроку і до останнього, через вже відому функцію 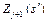 :
: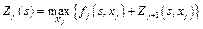
 . Зауважимо, що за аргумент функції
. Зауважимо, що за аргумент функції 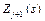 беремо не s, а змінений стан системи, тобто
беремо не s, а змінений стан системи, тобто 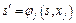 .
.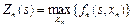
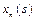 , завдяки якому цей максимум досягається.
, завдяки якому цей максимум досягається.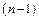 - го,
- го, 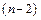 - го і т. д., тобто всіх попередніх кроків за рекурентними залежностями п.6, і для кожного кроку знаходимо умовне оптимальне управління:
- го і т. д., тобто всіх попередніх кроків за рекурентними залежностями п.6, і для кожного кроку знаходимо умовне оптимальне управління: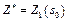
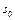 до кінцевого. Для цього з урахуванням визначеного оптимального управління на першому кроці
до кінцевого. Для цього з урахуванням визначеного оптимального управління на першому кроці 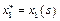 змінюємо стан системи згідно з п. 5. Далі для цього нового стану знаходимо оптимальне управління на другому кроці
змінюємо стан системи згідно з п. 5. Далі для цього нового стану знаходимо оптимальне управління на другому кроці 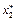 і діємо так до останнього кроку.
і діємо так до останнього кроку.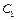
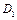


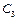
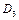
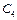
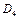
 — обсяг капіталовкладень, виділених на кроках 1—4;
— обсяг капіталовкладень, виділених на кроках 1—4;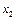 — те саме на кроках 2—4;
— те саме на кроках 2—4;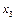 — те саме на кроках 3 і 4;
— те саме на кроках 3 і 4; — те саме на кроці 4.
— те саме на кроці 4. — обсяги інвестицій на г'-му підприємстві
— обсяги інвестицій на г'-му підприємстві  .
.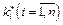 — оптимальні обсяги інвестицій на і- му підприємстві.
— оптимальні обсяги інвестицій на і- му підприємстві.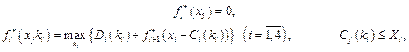
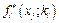 — сумарна ефективність інвестицій з і- го кроку до останнього.
— сумарна ефективність інвестицій з і- го кроку до останнього. , оскільки п'ятого підприємства не існує. Виконаємо поетапні розрахунки за цією моделлю.
, оскільки п'ятого підприємства не існує. Виконаємо поетапні розрахунки за цією моделлю.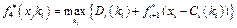
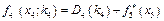
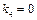
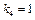
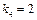

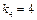
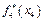

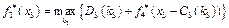

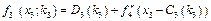
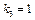
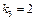
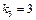
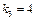
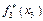
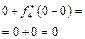
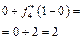
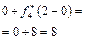
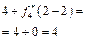
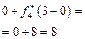
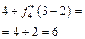
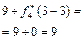
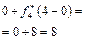
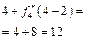
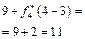
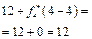
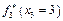 .
.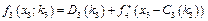 .
.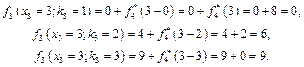
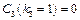 , оскільки для третього підприємства не існує проекту з інвестиціями в 1 млн грн. Значення
, оскільки для третього підприємства не існує проекту з інвестиціями в 1 млн грн. Значення 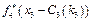 беремо з попередньої таблиці. Далі маємо:
беремо з попередньої таблиці. Далі маємо: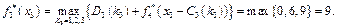
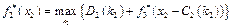

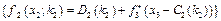
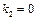
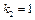
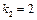
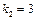
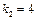
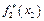
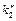
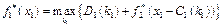

 , подаючи їх у вигляді таблиці:
, подаючи їх у вигляді таблиці: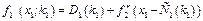
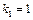
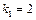
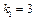
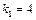
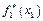
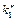

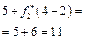
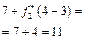
 , тобто для першого підприємства реалізується другий проект, який використовує 1 млн грн. інвестицій з ефективністю 3 млн грн. Отже,
, тобто для першого підприємства реалізується другий проект, який використовує 1 млн грн. інвестицій з ефективністю 3 млн грн. Отже, 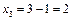 для другого, третього і четвертого підприємств залишається 4-1=3 млн грн. інвестицій. Із таблиці другого кроку маємо, що за умов
для другого, третього і четвертого підприємств залишається 4-1=3 млн грн. інвестицій. Із таблиці другого кроку маємо, що за умов 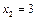 максимальний ефект настає в разі реалізації для другого підприємства першого проекту
максимальний ефект настає в разі реалізації для другого підприємства першого проекту 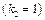 ефективність становить 4 млн грн. Отже,
ефективність становить 4 млн грн. Отже, 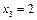 маємо, що
маємо, що 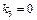 . Отже,
. Отже, 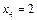 , а йому відповідають капітальні вкладення
, а йому відповідають капітальні вкладення