У цій главі ми вивчимо найпростіші статистичні алгоритми, головний з яких – визначення максимального й мінімального значення на безлічі даних.
Розглянемо алгоритм у загальному виді:
- описати для кожного максимуму й мінімуму по одній змінної того ж типу, що аналізовані дані;
- до циклу максимуму привласнюється або свідомо мале для аналізованих даних значення, або перший елемент даних; мінімуму привласнюється або свідомо велике для аналізованих даних значення, або перший елемент даних;
- у тілі циклу кожний підходящий для пошуку елемент даних t обробляється операторами виду:
if t>max then max:=t; - для максимуму;
if t<min then min:=t; - для мінімуму,
де max і min – змінні для максимуму й мінімуму відповідно.
Крок 2 цього алгоритму вимагає коментарів, які ми зробимо на прикладі пошуку максимуму. Очевидно, що сам алгоритм нескладний – кожний елемент даних t послідовно рівняється з коміркою пам'яті max і, якщо виявлене значення t, більше поточного значення max, воно заноситься в max оператором max:=t;. Як ми пам'ятаємо, після опису на кроці 1 змінної max, її значення ще не визначене, і може виявитися кожним – звідки випливає необхідність завдання початкового значення. Представимо, що після вибору початкового значення max, рівного нулю, при аналізі зустрілися тільки негативні значення елементів t. У цьому випадку умова t>max не виконається жодного разу й відповіддю буде max, рівне нулю, що неправильно! Вибір свідомо малого початкового значення max (наприклад, значення -1E30, тобто -1030, чи навряд зустрінеться в будь-яких реальних даних) гарантує, що умова t>max виконається хоча б раз і максимум буде знайдений. Альтернативний спосіб – привласнити max значення окремо обчисленого першого елемента послідовності даних. У цьому випадку відповідь або вже знайдений, якщо перший елемент і є максимальний, або буде знайдений у циклі.
Аналогічні міркування допомагають зрозуміти, чому мінімуму слід привласнювати в якості початкового значення свідомо велике число.
Перейдемо до прикладів.
Пр. Для функції y(x)=sin2(x), 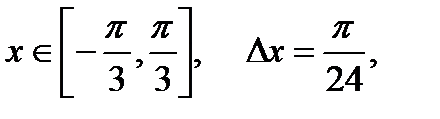 знайти мінімальне серед позитивних і максимальне значення.
знайти мінімальне серед позитивних і максимальне значення.
Позначивши шукані значення min і max відповідно, складемо наступну програму:
var x,y,max,min:real;
begin
x:=-pi/3;
max:=-2;
min:=2; {ці початкові значення - свідомо мале й велике для синуса}
while x<=pi/3+1e-6 do begin
y:=sqr(sin(x));
if y>0 then {шукаємо min тільки серед позитивних!}
if y<min then min:=y;
if y>max then max:=y;
x:=x+pi/24;
end;
writeln ('Мінімум =',min:8:2);
writeln ('Максимум=',max:8:2);
reset (input); readln;
end.
У наступному прикладі додатково збережемо значення аргументів функції, для яких знайдені мінімум і максимум.
Пр. Послідовність T(k) задана співвідношеннями T(k)=max(sin k, cos k), k=1,2,…,31. Знайти номери максимального й мінімального елементів послідовності.
Пошук номерів не позбавить нас від необхідності пошуку значень. Тому, крім змінних min і max, нам знадобляться дві Цілочисельні змінні для зберігання номерів мінімального й максимального значень, позначимо їх kmin і kmax відповідно. Звернете також увагу, що на кожному кроці циклу додатково буде потрібно знаходити максимальне зі значень sin(k) і cos(k), для занесення його в t.
var t,max,min:real;
k,kmin,kmax:integer;
begin
min:=1e30; {не визначаючи свідомо великого й малого для цих даних значень,}
max:=-1e30;{задаємо "надійні" значення, близькі до плюс і мінус нескінченності}
for k:=1 to 31 do begin
if sin(k)>cos(k) then t:=sin(k)
else t:=cos(k);
if t<min then begin
{ за умовою потрібні 2 оператора - збереження нового хв. значення}
{і збереження номера елемента, звідси операторные дужки!}
min:=t; kmin:=k;
end;
if t>max then begin
max:=t; kmax:=k;
end;
end;
writeln ('Номер хв. елемента =',kmin);
writeln ('Номер макс. елемента=',kmax);
reset (input); readln;
end.


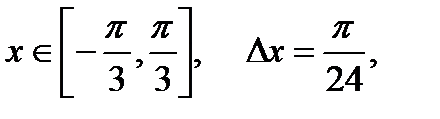 знайти мінімальне серед позитивних і максимальне значення.
знайти мінімальне серед позитивних і максимальне значення.