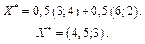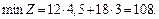Економічний зміст цього обмеження такий: фактичний час, витрачений на упакування продуктів А та В, не повинен перевищувати 10 год на день:
| Кількість сировини для продукту А –
- Витрати сировини під час обробки, тис. кг
| +
|
| Маса упаковки продукту А, тис. кг ×
×Продуктивність під час упакування продукту А, шт./год
|
| +
| Кількість сировини для продукту В, -
- Витрати сировини під час обробки, тис. кг
| £ 10 год
|
| Маса упаковки продукту В, тис. кг ×
× Продуктивність під час упакування продукту В, шт./год
|
Математично це запишеться так:
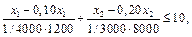
або
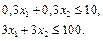
Побудуємо цільову функцію задачі. Прибуток фірми складається з різниці між доходом від реалізації виготовленої продукції та витратами на її виробництво.
1. Дохід, дол., від виробництва продуктів А та В визначається так:
| Кількість сировини, що надходить на упакування, тис. кг
| ×
| Ціна упаковки, дол.,
|
| Маса упаковки продукту, тис. кг
|
або
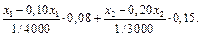
Загальний дохід дорівнює  .
.
2. Витрати, дол., на сировину визначаємо як загальну кількість сировини, тис. кг, використовуваної для виробництва продуктів А та В, помножену на вартість одиниці сировини, дол.:

3. Витрати, дол., пов'язані з використанням верстатів 1 і 2, визначаємо як фактичний час роботи верстата з обробки сировини, помножений на вартість 1 год роботи відповідного верстата:
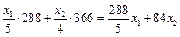
4. Витрати, дол., пов'язані з упакуванням продуктів А та В, складаються з фактичного часу роботи фабрики 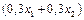 , помноженого на вартісний еквівалент 1 год роботи фабрики, який становить 360 дол.:
, помноженого на вартісний еквівалент 1 год роботи фабрики, який становить 360 дол.:

Узагальнюючи всі складові частини цільової функції, можемо записати математичний вираз прибутку фірми за день:

Отже, маємо остаточний запис економіко-математичної моделі:
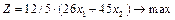
за обмежень
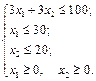
Незважаючи на порівняно складний процес моделювання, математично поставлена задача дуже проста й легко розв'язується графічно.
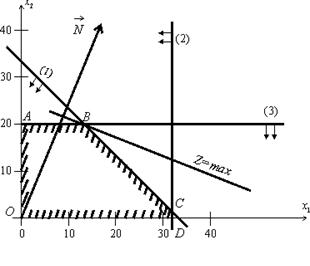
Розв'язування. Графічне розв'язування задачі ілюструє рис. 2.12. Областю допустимих планів, що утворюється системою обмежень задачі, є многокутник OABCD. Найбільшого значення цільова функція досягає у вершині В. Координати цієї точки визначаються із системи рівнянь:
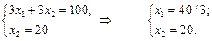
Оптимальний план задачі 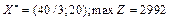 .
.
Отже, для того, щоб отримати найбільший денний прибуток 2992 дол., фірма має обробляти 40/3 тис. кг сировини, виробляючи продукт А, і 20 тис. кг — виробляючи продукт В. За такого оптимального плану випуску продукції верстат 2 працюватиме 20/4=5 год на день, тобто з повним навантаженням, а верстат 1 працюватиме лише 40/15 = 2 год 20 хв на день.
Задача 2.4.На меблевій фабриці зі стандартних листів фанери потрібно вирізати 24, 28 і 18 заготовок трьох розмірів. Лист фанери можна розрізати двома способами. Кількість отриманих заготовок та площу відходів за кожного способу розрізування одного листа фанери наведено в таблиці:
| Заготовка
| Кількість отриманих заготовок, шт., за способами
|
| першим
| другим
|
|
|
|
|
| Площа відходів, см2
|
|
|
Скільки листів фанери та за яким способом слід розрізати, щоб отримати потрібну кількість заготовок з мінімальними відходами.
Побудова математичної моделі. Нехай  — кількість листів фанери, які необхідно розрізати відповідно першим і другим способом.
— кількість листів фанери, які необхідно розрізати відповідно першим і другим способом.
Цільова функція — мінімізація відходів під час розрізування листа фанери. Математично це записується так:

Обмеження математичної моделі враховують кількість заготовок кожного виду, які потрібно отримати:
| для заготовки 1
для заготовки 2
для заготовки 3
| 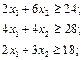
|
Отже, економіко-математична модель задачі має вигляд

за обмежень

Розв'язування. Графічне розв'язування задачі оптимального розрізування ілюструє рис. 2.13. Область допустимих розв'язків цієї задачі необмежена. Вектор  = (12; 18) можна змінити згідно з масштабом графіка, наприклад
= (12; 18) можна змінити згідно з масштабом графіка, наприклад  = (6; 9).
= (6; 9).
Із рис. 2.13 бачимо, що пряма 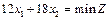 збігається зі стороною ВС многокутника розв'язків. Це означає, що задача має альтернативні оптимальні плани: координати будь-якої точки відрізка ВС є оптимальним планом, причому для цих координат цільова функція Z досягає свого найменшого значення. Визначимо лише два оптимальних плани, що відповідають кінцям відрізка ВС.
збігається зі стороною ВС многокутника розв'язків. Це означає, що задача має альтернативні оптимальні плани: координати будь-якої точки відрізка ВС є оптимальним планом, причому для цих координат цільова функція Z досягає свого найменшого значення. Визначимо лише два оптимальних плани, що відповідають кінцям відрізка ВС.

Точка В утворюється перетином прямих (2.29) і (2.30); її координати визначаємо із системи рівнянь

звідки  .
.
Точка С лежить на перетині прямих (2.28) і (2.30); її координати визначаємо із системи рівнянь
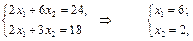
отже, 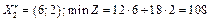 .
.
Повертаючись до економічного змісту розв'язаної задачі, маємо такі результати. Якщо розрізати 7 листів фанери, з яких 3 листи — першим способом, а 4 — другим, то матимемо найменшу площу відходів — 108 см. Але такі самі мінімальні втрати будуть і в разі розрізування шести листів першим способом і двох — другим.
Будь-який інший альтернативний оптимальний план задачі можна записати як опуклу лінійну комбінацію отриманих двох крайніх розв'язків:
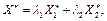
де 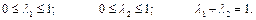 .
.
Наприклад, нехай 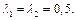 Тоді ще один оптимальний план задачі визначається так:
Тоді ще один оптимальний план задачі визначається так:
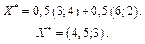
Цільова функція Z має таке саме мінімальне значення: 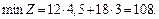
2.6. Симплексний метод розв'язування задач ЛП. Інші методи.


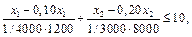
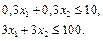
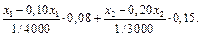
 .
.
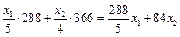
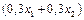 , помноженого на вартісний еквівалент 1 год роботи фабрики, який становить 360 дол.:
, помноженого на вартісний еквівалент 1 год роботи фабрики, який становить 360 дол.:

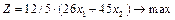
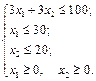
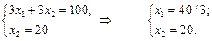

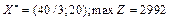 .
. — кількість листів фанери, які необхідно розрізати відповідно першим і другим способом.
— кількість листів фанери, які необхідно розрізати відповідно першим і другим способом.
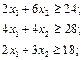


 = (12; 18) можна змінити згідно з масштабом графіка, наприклад
= (12; 18) можна змінити згідно з масштабом графіка, наприклад 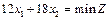 збігається зі стороною ВС многокутника розв'язків. Це означає, що задача має альтернативні оптимальні плани: координати будь-якої точки відрізка ВС є оптимальним планом, причому для цих координат цільова функція Z досягає свого найменшого значення. Визначимо лише два оптимальних плани, що відповідають кінцям відрізка ВС.
збігається зі стороною ВС многокутника розв'язків. Це означає, що задача має альтернативні оптимальні плани: координати будь-якої точки відрізка ВС є оптимальним планом, причому для цих координат цільова функція Z досягає свого найменшого значення. Визначимо лише два оптимальних плани, що відповідають кінцям відрізка ВС.

 .
.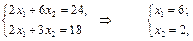
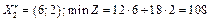 .
.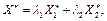
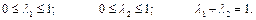 .
.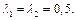 Тоді ще один оптимальний план задачі визначається так:
Тоді ще один оптимальний план задачі визначається так: