 Нехай маємо деяку цілочислову задачу лінійного програмування на максимум з двома змінними: x1 та x2..
Нехай маємо деяку цілочислову задачу лінійного програмування на максимум з двома змінними: x1 та x2..
Розглянемо спочатку геометричну інтерпретацію цієї задачі без врахування умови цілочисельності цих змінних. Тоді область допустимих розв’язків такої задачі буде представляти собою, як відомо, деякий опуклий багатокутник, наприклад, багатокутник ABCO (рис. 5.1). Цільова функція, як і раніше, буде представляти собою множину ліній рівня, кожна з яких відповідає деякому числовому значенню цільової функції. Тоді переміщуючи деяку початкову лінію рівня у напрямку зростання значення цільовою функції, тобто у напрямку вектору 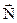 , отримаємо максимальне значення цільової функції у кутовій точці B.Координати цієї точки і є оптимальним планом задачі лінійного програмування без врахування умови цілочисельності. Нехай, при цьому,
, отримаємо максимальне значення цільової функції у кутовій точці B.Координати цієї точки і є оптимальним планом задачі лінійного програмування без врахування умови цілочисельності. Нехай, при цьому, 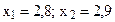 , тобто оптимальним планом задачі є вектор
, тобто оптимальним планом задачі є вектор 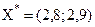 .
.
Тепер врахуємо додаткові умови цілочисельності, що накладаються на змінні задачі. Умова цілочисельності, призводить до того, що геометрично область допустимих розв’язків лінійної цілочислової задачі тепер буде представляти собою множину (систему) точок з цілочисловими координатами, що знаходяться всередині опуклого багатокутника допустимих розв’язків відповідної не цілочислової задачі. Тобто, для розглянутого на рис. 5.1 випадку множина допустимих планів складається тільки з дев’яти точок (рис. 5.2), які утворені перетинами сім’ї прямих, що паралельні осям Ох1 та Oх2 і проходять через точки з цілими координатами 0, 1, 2. Для знаходження цілочислового оптимального розв’язку лінію рівня, що відповідає цільовій функції, пересуваємо у напрямку вектора нормалі 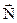 до перетину з кутовою точкою утвореної цілочислової сітки. Координати цієї точки і є оптимальним цілочисловим розв’язком задачі. У нашому прикладі оптимальний цілочисловий розв’язок відповідає точці М з координатами, тобто
до перетину з кутовою точкою утвореної цілочислової сітки. Координати цієї точки і є оптимальним цілочисловим розв’язком задачі. У нашому прикладі оптимальний цілочисловий розв’язок відповідає точці М з координатами, тобто 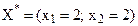 і оптимальний план цілочислової задачі лінійного програмування не співпадає з оптимальним планом задачі лінійного програмування.
і оптимальний план цілочислової задачі лінійного програмування не співпадає з оптимальним планом задачі лінійного програмування.
 Таким чином особливість геометричної інтерпретації цілочислової задачі у зіставленні зі звичайною задачею лінійного програмування полягає лише у визначенні множини допустимих розв’язків. Областю допустимих розв’язків загальної задачі лінійного програмування є опуклий багатогранник, а вимога цілочисельності розв’язку приводить до такої множини допустимих розв’язків, яка є дискретною і утворюється тільки з окремих точок.
Таким чином особливість геометричної інтерпретації цілочислової задачі у зіставленні зі звичайною задачею лінійного програмування полягає лише у визначенні множини допустимих розв’язків. Областю допустимих розв’язків загальної задачі лінійного програмування є опуклий багатогранник, а вимога цілочисельності розв’язку приводить до такої множини допустимих розв’язків, яка є дискретною і утворюється тільки з окремих точок.
Якщо у разі двох змінних розв’язок задачі можна відшукати графічним методом, тобто, використовуючи цілочислову сітку, можна досить просто знайти оптимальний план, то в іншому разі необхідно застосовувати спеціальні методи.
5.3. Загальна характеристика методів розв’язування цілочислових задач лінійного програмування
Для знаходження оптимального розв’язку цілочислових задач застосовують різні методи. Найпростішим з них є знаходження оптимального розв’язку задачі лінійного програмування як такої, що має лише неперервні (а не цілочислові змінні), з подальшим їх заокругленням. Такий підхід є виправданим тоді, коли змінні в оптимальному плані набувають досить великих значень у зіставленні їх з одиницями вимірювання. Нехай, наприклад, у результаті розв’язування задачі про поєднання галузей у сільськогосподарському підприємстві отримали оптимальне поголів’я корів — 1235,6. Заокругливши це значення до 1236, ми не зробимо значної похибки. Проте за інших умов такі спрощення призводять до істотних неточностей. Так, повертаючись до попереднього прикладу (рис. 5.1), бачимо, що максимальне значення функціонала для даної задачі знаходиться в точці В( 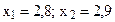 ). Заокруглення дасть таке значення оптимального плану
). Заокруглення дасть таке значення оптимального плану 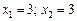 (точка D на рис. 5.1). Очевидно, що точка D не може бути розв’язком задачі, оскільки вона навіть не належить множині допустимих розв’язків (чотирикутник ОАВС), тобто відповідні значення змінних не задовольнятимуть систему обмежень задачі.
(точка D на рис. 5.1). Очевидно, що точка D не може бути розв’язком задачі, оскільки вона навіть не належить множині допустимих розв’язків (чотирикутник ОАВС), тобто відповідні значення змінних не задовольнятимуть систему обмежень задачі.
Для знаходження оптимальних планів задач цілочислового програмування застосовують такі групи спеціальних методів:
1) точні методи:
· методи відтинання;
· комбінаторні методи;
2) наближені методи.
Основою методів відтинання є ідея поступового «звуження» області допустимих розв’язків розглядуваної задачі. Пошук цілочислового оптимуму починається з розв’язування задачі з так званими послабленими обмеженнями, тобто без урахування вимог цілочисельності змінних. Далі введенням у модель спеціальних додаткових обмежень, що враховують цілочисельність змінних, багатогранник допустимих розв’язків послабленої задачі поступово зменшують доти, доки змінні оптимального розв’язку не набудуть цілочислових значень.
До цієї групи належать:
а) методи розв’язування повністю цілочислових задач (дробовий алгоритм Гоморі);
б) методи розв’язування частково цілочислових задач (другий алгоритм Гоморі, або змішаний алгоритм цілочислового програмування).
Комбінаторні методи цілочислової оптимізації базуються на ідеї перебору всіх допустимих цілочислових розв’язків, однак, згідно з їх процедурою здійснюється цілеспрямований перебір лише досить невеликої частини розв’язків. Найпоширенішим у цій групі методів є метод гілок і меж.
Починаючи з розв’язування послабленої задачі, він передбачає поділ початкової задачі на дві підзадачі через виключення областей, що не мають цілочислових розв’язків, і дослідження кожної окремої частини багатогранника допустимих розв’язків.
Для розв’язування задач із бінарними змінними застосовують комбінаторні методи, причому, оскільки змінні є бінарними, то методи пошуку оптимуму значно спрощуються.
Досить поширеними є також наближені методи розв’язування цілочислових задач лінійного програмування. Оскільки для практичних задач великої розмірності за допомогою точних методів не завжди можна знайти строго оптимальний розв’язок за прийнятний час або для розв’язування задачі використовуються наближено визначені, неточні початкові дані, то часто в реальних задачах досить обмежитися наближеним розв’язком, пошук якого є спрощеним.
Значна частина наближених алгоритмів базується на використанні обчислювальних схем відомих точних методів, таких, наприклад, як метод гілок і меж.
До наближених методів належать: метод локальної оптимізації (метод вектора спаду); модифікації точних методів; методи випадкового пошуку та ін.
Головними показниками для зіставлення ефективності застосування конкретних наближених алгоритмів на практиці є такі: абсолютна 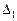 та відносна
та відносна 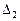 похибки отриманих наближених розв’язків.
похибки отриманих наближених розв’язків.
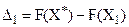 ,
, 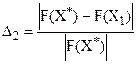 ,
,
де F — цільова функція (в даному разі для визначеності допускаємо вимогу відшукання максимального її значення); Х1— наближений розв’язок, знайдений деяким наближеним методом; Х* — оптимальний план задачі.
5.4. Методи відтинання. Метод Гоморі
В основу методів відтинання покладено ідею Данціга. Сутність цієї ідеї полягає у тому, що спочатку задача розв’язується без врахування умови цілочисельності, тобто як звичайна задача лінійного програмування. Якщо у результаті розв’язання такої задачі ми отримаємо цілочисловий оптимальний план, задача розв’язана. Якщо ж оптимальний план не є цілочисловим, до обмежень задачі додається нове обмеження, що має наступні властивості:
· воно повинно бути лінійним;
· воно повинно відтинати знайдений оптимальний не цілочисловий план;
· воно не повинно відтинати жодного цілочислового плану.
Таке додаткове обмеження, якому притаманні ці властивості, називається правильним відтинанням.
Далі задача розв’язується з врахуванням нового обмеження. Якщо її розв’язок знову не задовольняє умови цілочисельності, то будується нове додаткове обмеження, що відтинає отриманий розв’язок, не зачіпаючи цілочислових планів. Процес приєднання додаткових обмежень повторюють доти, доки не буде знайдено цілочислового оптимального плану, або доведено, що його не існує.
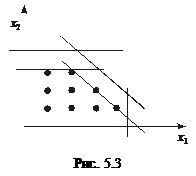 Геометрично введення додаткового лінійного обмеження означає проведення гіперплощини (прямої), що відтинає від багатогранника (багатокутника) допустимих розв’язків задачі ту його частину, яка містить точки з нецілочисловими координатами, однак не зачіпає жодної цілочислової точки даної множини. Отриманий новий багатогранник розв’язків містить всі цілі точки, які були в початковому, і розв’язок, що буде отримано на ньому, буде цілочисловим (рис. 5.3).
Геометрично введення додаткового лінійного обмеження означає проведення гіперплощини (прямої), що відтинає від багатогранника (багатокутника) допустимих розв’язків задачі ту його частину, яка містить точки з нецілочисловими координатами, однак не зачіпає жодної цілочислової точки даної множини. Отриманий новий багатогранник розв’язків містить всі цілі точки, які були в початковому, і розв’язок, що буде отримано на ньому, буде цілочисловим (рис. 5.3).
Слід відмітити, що визначення правила для реалізації ідеї Данціга стосовно формування додаткового обмеження виявилось досить складним завданням і першим, кому вдалось успішно реалізувати цю ідею, був Гоморі.
Розглянемо алгоритм, запропонований Гоморі, для розв’язування повністю цілочислової задачі лінійного програмування, що ґрунтується на використанні симплексного методу і передбачає застосування досить простого способу побудови правильного відтинання.
Нехай маємо задачу цілочислового програмування:
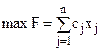 ( 5.5 )
( 5.5 )
за умов:
 ,
, 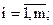 ( 5.6 )
( 5.6 )
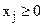 ,
, 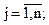 ( 5.7 )
( 5.7 )
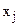 — цілі числа
— цілі числа 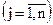 . ( 5.8 )
. ( 5.8 )
Допустимо, що параметри 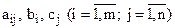 — цілі числа.
— цілі числа.
Не враховуючи умови цілочисельності, знаходимо розв’язок задачі (5.5)—(5.7) симплексним методом. Нехай розв’язок існує і міститься в такій симплексній таблиці:
Таблиця 5.1
| Базис
| Сбаз
| План
| c1
| c2
| ...
| cm
| cm + 1
| ...
| cn
|
| х1
| х2
| ...
| хm
| хm + 1
| ...
| хn
|
| х1
| c1
| b1
|
|
| ...
|
| a1m + 1
| ...
| a1n
|
| х2
| c2
| b2
|
|
| ...
|
| a2m + 1
| ...
| a2n
|
| ...
| ...
| ...
| ...
| ...
| ...
| ...
| ...
| ...
| ...
|
| хm
| cm
| bm
|
|
| ...
|
| amm + 1
| ...
| amn
|
Змінні 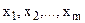 — базисні, а
— базисні, а 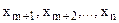 — вільні. Оптимальний план задачі:
— вільні. Оптимальний план задачі: 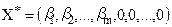 . Якщо
. Якщо 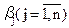 — цілі числа, то отриманий розв’язок є цілочисловим оптимальним планом задачі (5.5)—(5.8). Інакше існує хоча б одне з чисел, наприклад,
— цілі числа, то отриманий розв’язок є цілочисловим оптимальним планом задачі (5.5)—(5.8). Інакше існує хоча б одне з чисел, наприклад, 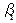 — дробове. Отже, необхідно побудувати правильне обмеження, що відтинає нецілу частину значення
— дробове. Отже, необхідно побудувати правильне обмеження, що відтинає нецілу частину значення 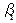 .
.
Розглянемо довільний оптимальний план 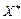 задачі (5.5) —(5.7). Виразимо в цьому плані базисну змінну
задачі (5.5) —(5.7). Виразимо в цьому плані базисну змінну 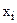 через вільні змінні:
через вільні змінні:
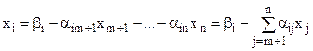 . (5.9)
. (5.9)
Виразимо коефіцієнти при змінних даного рівняння у вигляді суми їх цілої та дробової частин. Введемо позначення: 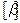 — ціла частина числа b,
— ціла частина числа b, 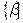 — дробова частина числа b[1]. Отримаємо:
— дробова частина числа b[1]. Отримаємо:
 , (5.10)
, (5.10)
або
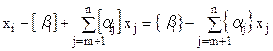 . (5.11)
. (5.11)
Отже, рівняння (6.11) виконується для будь-якого допустимого плану задачі (5.5)—(5.7). Допустимо тепер, що розглянутий план  є цілочисловим оптимальним планом задачі. Тоді ліва частина рівняння (5.11) складається лише з цілих чисел і є цілочисловим виразом. Отже, права його частина також є цілим числом і справджується рівність:
є цілочисловим оптимальним планом задачі. Тоді ліва частина рівняння (5.11) складається лише з цілих чисел і є цілочисловим виразом. Отже, права його частина також є цілим числом і справджується рівність:
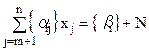 , (5.12)
, (5.12)
де N — деяке ціле число.
Величина N не може бути від’ємною. Якщо б  , то з рівняння (5.12) приходимо до нерівності:
, то з рівняння (5.12) приходимо до нерівності:
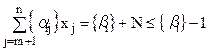 .
.
Звідки 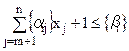 . Тобто це означало б, що дробова частина
. Тобто це означало б, що дробова частина 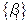 перевищує одиницю, що неможливо. У такий спосіб доведено, що число N є невід’ємним.
перевищує одиницю, що неможливо. У такий спосіб доведено, що число N є невід’ємним.
Якщо від лівої частини рівняння (6.12) відняти деяке невід’ємне число, то приходимо до нерівності:
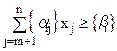 , (5.13)
, (5.13)
яка виконується за допущенням для будь-якого цілочислового плану задачі (5.5)—(5.7). У такий спосіб виявилося, що нерівність (5.13) є шуканим правильним відтинанням.
Отже, для розв’язування цілочислових задач лінійного програмування (5.1)—(5.4) методом Гоморі застосовують такий алгоритм:
1. Симплексним методом розв’язується задача без вимог цілочисельності змінних — (5.1)—(5.3).
Якщо серед елементів умовно-оптимального плану немає дробових чисел, то цей план є розв’язком задачі цілочислового програмування (5.1)—(5.4).
Якщо задача (5.1)—(5.3) не має розв’язку (цільова функція необмежена, або система обмежень несумісна), то задача (5.1) — (5.4) також не має розв’язку.
2. Коли в умовно-оптимальному плані є дробові значення, то вибирається змінна, яка має найбільшу дробову частину. На базі цієї змінної (елементів відповідного рядка останньої симплексної таблиці, в якому вона міститься) будується додаткове обмеження Гоморі:
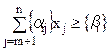 .
.
3. Додаткове обмеження після зведення його до канонічного вигляду і введення базисного елемента приєднується до останньої симплексної таблиці, яка містить умовно-оптимальний план. Отриману розширену задачу розв’язують і перевіряють її розв’язок на цілочисельність. Якщо він не цілочисловий, то процедуру повторюють, повертаючись до п. 2. Так діють доти, доки не буде знайдено цілочислового розв’язку або доведено, що задача не має допустимих розв’язків на множині цілих чисел.
У літературі доведено, що за певних умов алгоритм Гоморі є скінченим, але процес розв’язування задач великої розмірності методом Гоморі повільно збіжний. Слід також мати на увазі, що і кількість ітерацій суттєво залежить від сформованого правильного відтинання. Наведене правило (5.13) щодо формування правильного відтинання не єдине. Існують ефективніші відтинання, які використовуються у другому та третьому алгоритмах Гоморі, однак наявний практичний досвід ще не дає змоги виділити з них найкращий.
Загалом, алгоритм Гоморі в обчислювальному аспекті є мало вивченим. Якщо в лінійному програмуванні спостерігається відносно жорстка залежність між кількістю обмежень задачі та кількістю ітерацій, що необхідна для її розв’язування, то для цілочислових задач такої залежності не існує. Кількість змінних також мало впливає на трудомісткість обчислень. Очевидно, процес розв’язання цілочислової задачі визначається не лише її розмірністю, а також особливостями багатогранника допустимих розв’язків, що являє собою набір ізольованих точок.
Як правило, розв’язування задач цілочислового програмування потребує великого обсягу обчислень. Тому при створенні програм для ЕОМ особливу увагу слід приділяти засобам, що дають змогу зменшити помилки округлення, які можуть призвести до того, що отриманий цілочисловий план не буде оптимальним.
5.5. Комбінаторні методи.
Метод гілок та меж
В основу комбінаторних методів покладено перебір можливих варіантів розв’язків поставленої задачі. Кожен з них характеризується певною послідовністю перебору варіантів та правилами виключення, що дають змогу ще в процесі розв’язування задачі виявити неоптимальні варіанти без попередньої їх перевірки. Відносна ефективність різних методів залежить від того, наскільки кожен з них уможливлює скорочення необхідного процесу перебору варіантів у результаті застосування правила виключення.
Розглянемо один із комбінаторних методів - метод гілок і меж, який є більш ефективним за метод Гоморі. Спочатку, як і в разі методу Гоморі, симплексним методом розв’язується послаблена (без умов цілочисельності) задача. Потім вводиться правило перебору.
Нехай потрібно знайти хj — цілочислову змінну, значення якої хj= 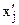 в оптимальному плані послабленої задачі є дробовим. Очевидно, що в деякому околі даної точки також не існує цілочислових значень, тому відповідний проміжок можна виключити з множини допустимих планів задачі в подальшому розгляді. Таким проміжком є інтервал між найближчими до
в оптимальному плані послабленої задачі є дробовим. Очевидно, що в деякому околі даної точки також не існує цілочислових значень, тому відповідний проміжок можна виключити з множини допустимих планів задачі в подальшому розгляді. Таким проміжком є інтервал між найближчими до 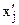 цілочисловими значеннями. Можна стверджувати, що на інтервалі
цілочисловими значеннями. Можна стверджувати, що на інтервалі 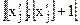 цілих значень немає.
цілих значень немає.
Наприклад, якщо 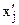 =2,7 дістаємо інтервал
=2,7 дістаємо інтервал 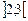 , де, очевидно, немає хj, яке набуває цілого значення і оптимальний розв’язок буде знаходитися або в інтервалі
, де, очевидно, немає хj, яке набуває цілого значення і оптимальний розв’язок буде знаходитися або в інтервалі  , або
, або 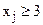 . Виключення проміжку
. Виключення проміжку 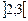 з множини допустимих планів здійснюється введенням до системи обмежень початкової задачі додаткових нерівностей. Тобто допустиме ціле значення xj має задовольняти одну з нерівностей виду:
з множини допустимих планів здійснюється введенням до системи обмежень початкової задачі додаткових нерівностей. Тобто допустиме ціле значення xj має задовольняти одну з нерівностей виду:
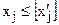 або
або 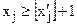 .
.
Дописавши кожну з цих умов до задачі з послабленими обмеженнями, дістанемо дві, не пов’язані між собою, задачі. Тобто, початкову задачу цілочислового програмування (5.1)—(5.4) поділимо на дві задачі з урахуванням умов цілочисельності змінних, значення яких в оптимальному плані послабленої задачі є дробовими. Це означає, що симплекс-методом розв’язуватимемо дві такі задачі:
перша задача: 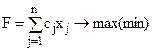 (5.14)
(5.14)
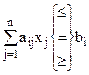 ,
, 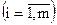 , (5.15)
, (5.15)
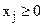 ,
, 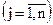 , (5.16)
, (5.16)
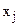 — цілі числа,
— цілі числа, 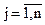 , (5.17)
, (5.17)
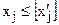 , (5.18)
, (5.18)
друга задача
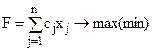 (5.19)
(5.19)
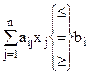 ,
, 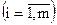 , (5.20)
, (5.20)
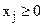 ,
, 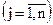 , (5.21)
, (5.21)
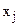 — цілі числа
— цілі числа 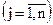 , (5.22)
, (5.22)
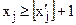 , (5.23)
, (5.23)
де 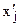 — не цілочислова компонента розв’язку задачі (5.1)—(5.4).
— не цілочислова компонента розв’язку задачі (5.1)—(5.4).
Наведені задачі (5.14)—(5.18) і (5.19)—(5.23) спочатку послаблюємо, тобто розв’язуємо з відкиданням обмежень (5.17) і (5.22). Якщо знайдені оптимальні плани задовольняють умови цілочисельності, то ці плани є розв’язками задачі (5.1)—(5.4). Інакше пошук розв’язку задачі триває. Для дальшого розгалуження вибираємо розв’язок задачі з більшим значенням цільової функції, якщо йдеться про максимізацію, і навпаки — з меншим значенням цільової функції в разі її мінімізації. Подальше розгалуження виконується доти, доки не буде встановлено неможливість поліпшення розв’язку. Здобутий останній план — оптимальний.
Розв’язування цілочислових задач методом гілок і меж можна значно прискорити. Очевидно, що кожна наступна задача, яку отримують в процесі розв’язування відрізняється від попередньої лише одним обмеженням. Тому за послідовного розв’язування задач немає сенсу розв’язувати їх симплексним методом спочатку. Досить буде почергово приєднати нові обмеження виду (5.18) і (5.23) до останньої симплекс-таблиці попередньої задачі та вилучити (в разі необхідності) непотрібні «старі» обмеження.
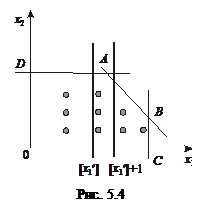 Геометрично введення додаткових лінійних обмежень виду (5.18) та (5.23) в систему обмежень початкової задачі означає проведення гіперплощин (прямих), що розтинають багатогранник (багатокутник) допустимих планів відповідної задачі лінійного програмування у такий спосіб, що уможливлюється включення в план найближчої цілої точки цього багатокутника (рис. 5.4). Допустимо, що А — точка максимуму, тоді за методом гілок та меж багатокутник допустимих планів задачі ABCOD поділяється на дві частини прямими
Геометрично введення додаткових лінійних обмежень виду (5.18) та (5.23) в систему обмежень початкової задачі означає проведення гіперплощин (прямих), що розтинають багатогранник (багатокутник) допустимих планів відповідної задачі лінійного програмування у такий спосіб, що уможливлюється включення в план найближчої цілої точки цього багатокутника (рис. 5.4). Допустимо, що А — точка максимуму, тоді за методом гілок та меж багатокутник допустимих планів задачі ABCOD поділяється на дві частини прямими 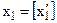 та
та 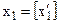 +1, що виключає з розгляду точку А, координата якої
+1, що виключає з розгляду точку А, координата якої 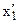 є не цілим числом.
є не цілим числом.
Опишемо алгоритм методу гілок та меж:
1. Симплексним методом розв’язують задачу (5.1)—(5.3) (без вимог цілочисельності змінних).
Якщо серед елементів умовно-оптимального плану немає дробових чисел, то цей розв’язок є оптимальним планом задачі цілочислового програмування (5.1)—(5.4).
Якщо задача (5.1)—(5.3) не має розв’язку (цільова функція необмежена, або система обмежень несумісна), то задача (5.1)—(5.4) також не має розв’язку.
2. Коли в умовно-оптимальному плані є дробові значення, то вибирають одну з нецілочислових змінних 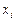 і визначають її цілу частину
і визначають її цілу частину 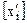 .
.
3. Записують два обмеження, що відтинають нецілочислові розв’язки:
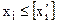 ,
,
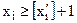 .
.
4. Кожну з одержаних нерівностей приєднують до обмежень початкової задачі. В результаті отримують дві нові цілочислові задачі лінійного програмування.
5. У будь-якій послідовності розв’язують обидві задачі.
У разі, коли отримано цілочисловий розв’язок хоча б однієї із задач, значення цільової функції цієї задачі зіставляють з початковим значенням. Якщо різниця не більша від заданого числа e, то процес розв’язування може бути закінчено. У разі, коли цілочисловий розв’язок одержано в обох задачах, то з розв’язком початкової зіставляється той, який дає краще значення цільової функції. Якщо ж в обох задачах одержано нецілочислові розв’язки, то для дальшого гілкування вибирають ту задачу, для якої здобуто краще значення цільової функції і здійснюють перехід до кроку 2.


 Нехай маємо деяку цілочислову задачу лінійного програмування на максимум з двома змінними: x1 та x2..
Нехай маємо деяку цілочислову задачу лінійного програмування на максимум з двома змінними: x1 та x2..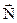 , отримаємо максимальне значення цільової функції у кутовій точці B.Координати цієї точки і є оптимальним планом задачі лінійного програмування без врахування умови цілочисельності. Нехай, при цьому,
, отримаємо максимальне значення цільової функції у кутовій точці B.Координати цієї точки і є оптимальним планом задачі лінійного програмування без врахування умови цілочисельності. Нехай, при цьому, 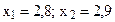 , тобто оптимальним планом задачі є вектор
, тобто оптимальним планом задачі є вектор 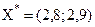 .
.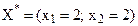 і оптимальний план цілочислової задачі лінійного програмування не співпадає з оптимальним планом задачі лінійного програмування.
і оптимальний план цілочислової задачі лінійного програмування не співпадає з оптимальним планом задачі лінійного програмування. Таким чином особливість геометричної інтерпретації цілочислової задачі у зіставленні зі звичайною задачею лінійного програмування полягає лише у визначенні множини допустимих розв’язків. Областю допустимих розв’язків загальної задачі лінійного програмування є опуклий багатогранник, а вимога цілочисельності розв’язку приводить до такої множини допустимих розв’язків, яка є дискретною і утворюється тільки з окремих точок.
Таким чином особливість геометричної інтерпретації цілочислової задачі у зіставленні зі звичайною задачею лінійного програмування полягає лише у визначенні множини допустимих розв’язків. Областю допустимих розв’язків загальної задачі лінійного програмування є опуклий багатогранник, а вимога цілочисельності розв’язку приводить до такої множини допустимих розв’язків, яка є дискретною і утворюється тільки з окремих точок.
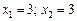 (точка D на рис. 5.1). Очевидно, що точка D не може бути розв’язком задачі, оскільки вона навіть не належить множині допустимих розв’язків (чотирикутник ОАВС), тобто відповідні значення змінних не задовольнятимуть систему обмежень задачі.
(точка D на рис. 5.1). Очевидно, що точка D не може бути розв’язком задачі, оскільки вона навіть не належить множині допустимих розв’язків (чотирикутник ОАВС), тобто відповідні значення змінних не задовольнятимуть систему обмежень задачі.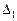 та відносна
та відносна 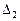 похибки отриманих наближених розв’язків.
похибки отриманих наближених розв’язків.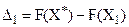 ,
, 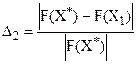 ,
, Геометрично введення додаткового лінійного обмеження означає проведення гіперплощини (прямої), що відтинає від багатогранника (багатокутника) допустимих розв’язків задачі ту його частину, яка містить точки з нецілочисловими координатами, однак не зачіпає жодної цілочислової точки даної множини. Отриманий новий багатогранник розв’язків містить всі цілі точки, які були в початковому, і розв’язок, що буде отримано на ньому, буде цілочисловим (рис. 5.3).
Геометрично введення додаткового лінійного обмеження означає проведення гіперплощини (прямої), що відтинає від багатогранника (багатокутника) допустимих розв’язків задачі ту його частину, яка містить точки з нецілочисловими координатами, однак не зачіпає жодної цілочислової точки даної множини. Отриманий новий багатогранник розв’язків містить всі цілі точки, які були в початковому, і розв’язок, що буде отримано на ньому, буде цілочисловим (рис. 5.3).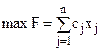 ( 5.5 )
( 5.5 ) ,
, 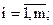 ( 5.6 )
( 5.6 )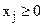 ,
, 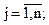 ( 5.7 )
( 5.7 )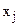 — цілі числа
— цілі числа 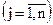 . ( 5.8 )
. ( 5.8 )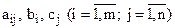 — цілі числа.
— цілі числа.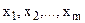 — базисні, а
— базисні, а 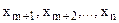 — вільні. Оптимальний план задачі:
— вільні. Оптимальний план задачі: 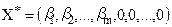 . Якщо
. Якщо 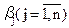 — цілі числа, то отриманий розв’язок є цілочисловим оптимальним планом задачі (5.5)—(5.8). Інакше існує хоча б одне з чисел, наприклад,
— цілі числа, то отриманий розв’язок є цілочисловим оптимальним планом задачі (5.5)—(5.8). Інакше існує хоча б одне з чисел, наприклад, 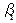 — дробове. Отже, необхідно побудувати правильне обмеження, що відтинає нецілу частину значення
— дробове. Отже, необхідно побудувати правильне обмеження, що відтинає нецілу частину значення 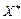 задачі (5.5) —(5.7). Виразимо в цьому плані базисну змінну
задачі (5.5) —(5.7). Виразимо в цьому плані базисну змінну 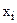 через вільні змінні:
через вільні змінні: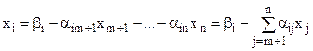 . (5.9)
. (5.9)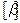 — ціла частина числа b,
— ціла частина числа b, 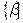 — дробова частина числа b[1]. Отримаємо:
— дробова частина числа b[1]. Отримаємо: , (5.10)
, (5.10)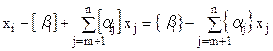 . (5.11)
. (5.11) є цілочисловим оптимальним планом задачі. Тоді ліва частина рівняння (5.11) складається лише з цілих чисел і є цілочисловим виразом. Отже, права його частина також є цілим числом і справджується рівність:
є цілочисловим оптимальним планом задачі. Тоді ліва частина рівняння (5.11) складається лише з цілих чисел і є цілочисловим виразом. Отже, права його частина також є цілим числом і справджується рівність: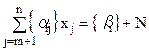 , (5.12)
, (5.12) , то з рівняння (5.12) приходимо до нерівності:
, то з рівняння (5.12) приходимо до нерівності: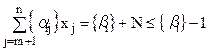 .
.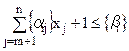 . Тобто це означало б, що дробова частина
. Тобто це означало б, що дробова частина 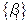 перевищує одиницю, що неможливо. У такий спосіб доведено, що число N є невід’ємним.
перевищує одиницю, що неможливо. У такий спосіб доведено, що число N є невід’ємним.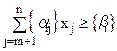 , (5.13)
, (5.13)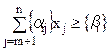 .
.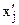 в оптимальному плані послабленої задачі є дробовим. Очевидно, що в деякому околі даної точки також не існує цілочислових значень, тому відповідний проміжок можна виключити з множини допустимих планів задачі в подальшому розгляді. Таким проміжком є інтервал між найближчими до
в оптимальному плані послабленої задачі є дробовим. Очевидно, що в деякому околі даної точки також не існує цілочислових значень, тому відповідний проміжок можна виключити з множини допустимих планів задачі в подальшому розгляді. Таким проміжком є інтервал між найближчими до 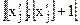 цілих значень немає.
цілих значень немає.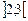 , де, очевидно, немає хj, яке набуває цілого значення і оптимальний розв’язок буде знаходитися або в інтервалі
, де, очевидно, немає хj, яке набуває цілого значення і оптимальний розв’язок буде знаходитися або в інтервалі  , або
, або 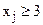 . Виключення проміжку
. Виключення проміжку 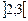 з множини допустимих планів здійснюється введенням до системи обмежень початкової задачі додаткових нерівностей. Тобто допустиме ціле значення xj має задовольняти одну з нерівностей виду:
з множини допустимих планів здійснюється введенням до системи обмежень початкової задачі додаткових нерівностей. Тобто допустиме ціле значення xj має задовольняти одну з нерівностей виду: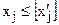 або
або 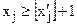 .
.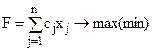 (5.14)
(5.14)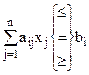 ,
, 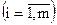 , (5.15)
, (5.15)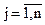 , (5.17)
, (5.17)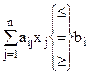 ,
, 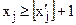 , (5.23)
, (5.23)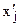 — не цілочислова компонента розв’язку задачі (5.1)—(5.4).
— не цілочислова компонента розв’язку задачі (5.1)—(5.4). Геометрично введення додаткових лінійних обмежень виду (5.18) та (5.23) в систему обмежень початкової задачі означає проведення гіперплощин (прямих), що розтинають багатогранник (багатокутник) допустимих планів відповідної задачі лінійного програмування у такий спосіб, що уможливлюється включення в план найближчої цілої точки цього багатокутника (рис. 5.4). Допустимо, що А — точка максимуму, тоді за методом гілок та меж багатокутник допустимих планів задачі ABCOD поділяється на дві частини прямими
Геометрично введення додаткових лінійних обмежень виду (5.18) та (5.23) в систему обмежень початкової задачі означає проведення гіперплощин (прямих), що розтинають багатогранник (багатокутник) допустимих планів відповідної задачі лінійного програмування у такий спосіб, що уможливлюється включення в план найближчої цілої точки цього багатокутника (рис. 5.4). Допустимо, що А — точка максимуму, тоді за методом гілок та меж багатокутник допустимих планів задачі ABCOD поділяється на дві частини прямими 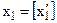 та
та 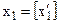 +1, що виключає з розгляду точку А, координата якої
+1, що виключає з розгляду точку А, координата якої 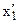 є не цілим числом.
є не цілим числом.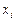 і визначають її цілу частину
і визначають її цілу частину 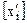 .
.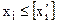 ,
,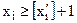 .
.