Изоляторы изготавливаются из фарфора или закаленного стекла и бывают двух видов: штыревые – для линий до 1 кВ и 6 –35 кВ; на линиях 35 кВ они применяются редко – только для малых сечений; подвесные - для линий 35 кВ и выше. Подвесные изоляторы собираются в подддерживающие провод гирлянды на промежуточных опорах, а натяжные гирлянды – на анкерных опорах.
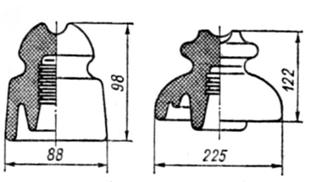
а) б)
а - напряжением до 1 кВ; б - напряжением 10 кВ
Рисунок 2.4 - Штыревые фарфоровые изоляторы
В подвесных гирляндах провод только поддерживается с помощью зажимов, в натяжных – закрепляется наглухо. Натяжные гирлянды находятся в более тяжелых условиях, чем подддерживающие. Поэтому на линиях до 110 кВ число изоляторов принимается на один больше.
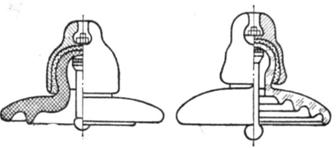
а) б)
Рисунок 2. 5 - Подвесные изоляторы ПФ (а) и ПС (б)
В последнее время в эксплуатации широко применяются длинностержневые изоляторы на основе высокопрочных стержней из стеклопластика с полимерным защитным покрытием (см. рисунок 2.6).
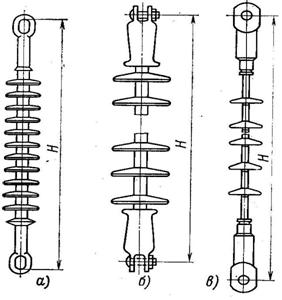
а) – с тарелками из этиленпропиленовых мономеров; б – с развитой поверхностью
из кремнийорганической резины; в) – с фторопластовым защитным покрытием стержня и фторопластовыми тарелками
Рисунок 2.6 – Полимерные изоляторы
Современный полимерный изолятор представляет собой комбинированную конструкцию, части которой выполняют свои определенные функции. В качестве несущего компонента изолятора применяется однонаправленный стеклопластиковый стержень. Он состоит из десятков тысяч тончайших стеклянных волокон, соединенных вместе полимерным связующим составом и обладающих высокой механической прочностью. Для увеличения длины пути утечки тока по поверхности изолятора с целью обеспечения его надежной работы в условиях загрязненной атмосферы к стеклопластиковому стержню прикрепляются изолирующие тарелки. Тарелки закрепляются на оболочке, защи-
щающей несущий стеклопластиковый стержень от всех видов коррозии, атмосферных и химических воздействий. Металлические оконцеватели, армируе
мые на концах несущего стержня изолятора, обеспечивают необходимую прочность и надежность изолятора. Такие изоляторы позволяют заменить целые гирлянды на ВЛ соответствующих классов напряжения и, таким образом, обеспечить надежность ВЛ. Масса полимерных изоляторов в 5 – 20 раз меньше массы соответствующих гирлянд тарелочных изоляторов. Это обеспечивает преимущества таких изоляторов при транспортировании, монтаже и эксплуатации ВЛ.
2.2 Основные сведения о конструкции кабелей
Силовые кабели состоят из одной или нескольких токоведущих жил, отделенных друг от друга и от земли изоляцией. Поверх изоляции для ее предохранения от влаги, кислот и механических повреждений накладывают защитную оболочку и стальную ленточную броню с защитными покровами. Токоведущие жилы, как правило, изготавливаются из алюминия как однопроволочными (сечением до 16 мм2 ), так и многопроволочными.
Изоляция выполняется из специальной пропитанной минеральным маслом кабельной бумаги, накладываемой в виде лент на токоведущие жилы. При прокладке кабелей на вертикальных и крутонаклонных трассах возможно перемещение пропитывающего состава вдоль кабеля. Поэтому для таких трасс изготавливаются кабели с обедненно-пропитанной изоляцией и с нестекающим пропитывающим составом. Изготавливаются также кабели с резиновой или полиэтиленовой изоляцией.
Защитные оболочки, накладываемые поверх изоляции для ее предохранения от влаги и воздуха, бывают свинцовыми, алюминиевыми или поливинилхлоридными. Рекомендуется широко использовать кабели в алюминиевой оболочке. Кабели в свинцовой оболочке предусмотрены для прокладки под водой, в угольных и сланцевых шахтах, в особо опасных коррозионно- активных средах. В остальных случаях выбор кабелей в свинцовой оболочке необходимо специально технически обосновать.
Свинцовые, алюминиевые или поливинилхлоридные оболочки надо защитить от механических повреждений. Для этого на оболочку накладывают броню из стальных лент или проволок. Алюминиевая оболочка и стальная броня в свою очередь подлежат защите от коррозии и химического воздействия. Для этого между оболочкой и броней, а также поверх брони накладывают внутренний и внешний защитные покровы. Внутренний защитный покров (или подушка под броней) – это джутовая прослойка из хлопчатобумажной пропитанной пряжи или из кабельной сульфатной бумаги. Поверх этой бумаги накладывают еще две поливинилхлоридные ленты. Наружный защитный покров также из джута, пропитанного антикоррозийным составом. Для прокладки в туннелях и других местах, опасных в пожарном отношении, применяют специальные кабели с негорючими защитными покровами.
На рисунке 2.7 показан трехжильный кабель 1 – 10 кВ с бумажной изоляцией.

1 – алюминиевые токоведущие жилы; 2 – бумага, пропитанная маслом (фазная изоляция ); 3- джутовые заполнители; 4 – бумага, пропитанная маслом (поясная изоляция); 5 – свинцовая или алюминиевая оболочка; 6 – прослойка из джута; 7 – стальная ленточная броня; 8 - джутовый покров.
Рисунок 2.7 -Устройство трехжильного кабеля напряжением 1-10 кВ с секторными жилами
Марки кабелей состоят из начальных букв слов, характеризующих их конструкцию. Первая буква А соответствует алюминиевым жилам. Оболочки кабелей обозначаются буквами: А – алюминиевая, С – свинцовая, В – поливинилхлоридная, Н – резиновая, наиритовая; П – полиэтиленовая; кабели с отдельно освинцованными жилами маркируются буквой О. Обозначения марок кабелей с различными бронированными защитными покровами отмечаются следующими буквами: Б – стальные ленты, П – плоские стальные оцинкованные проволоки, К - такие же проволоки, но круглые.
Рядом с маркой кабеля обычно указывают число и сечение токоведущих жил кабеля. Например, ААБ 3х120 означает: кабель с алюминиевыми жилами в алюминиевой оболочке, бронированный стальными лентами, с тремя жилами сечением 120 мм2.
В последнее время широко применяются в эксплуатации кабели с изоляцией из сшитого полиэтилена (см. рисунок 2.8).
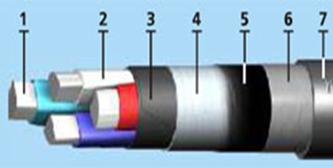
1 – токопроводящая жила; 2 – изоляция из сшитого полиэтилена; 3 – поясная изоляция; 4 – скрепляющая лента из нетканного полотна; 5 – поясная изоляция из полиэтилена; 6 – броня из двух стальных лент; 7 – битум; 8 – обмотка из полиэтилентерефталатной пленки; 9 – оболочка из полиэтилена.
Рисунок 2.8 – Конструкция кабеля с изоляцией из сшитого полиэтилена
В настоящее время в промышленно развитых странах Европы и Америки практически 100% рынка силовых кабелей занимают кабели с изоляцией из сшитого полиэтилена. Переход от кабелей с бумажной пропитанной изоляцией к кабелям с изоляцией из сшитого полиэтилена, связан со всё возрастающими требованиями эксплуатирующих организаций к техническим параметрам кабелей. В этом отношении преимущества этих кабелей очевидны.
Рассмотрим некоторые из них:
- высокая пропускная способность;
- малый вес, меньший диаметр и радиус изгиба;
- низкая повреждаемость;
- полиэтиленовая изоляция обладает малой плотностью, малыми значениями относительной диэлектрической проницаемости и коэффициента диэлектрических потерь;
- прокладка на сложных трассах;
- монтаж без использования специального оборудования;
- значительное снижение себестоимости прокладки.
Своими уникальными свойствами кабели с изоляцией из сшитого полиэтилена обязаны применяемому изоляционному материалу. Полиэтилен в настоящее время является одним из наиболее применяемых изоляционных материалов при производстве кабелей. Но изначально термопластичному полиэтилену присущи серьезные недостатки, главным из которых является резкое
ухудшение механических свойств при температурах, близких к температуре плавления. Решением этой проблемы стало применение сшитого полиэтилена.
3 Характеристики и параметры элементов электрической сети
3.1 Схемы замещения, параметры воздушных и кабельных линий
В большинстве случаев можно считать, что параметры линии электропередачи (активное и реактивное сопротивление, активная и емкостная проводимости) равномерно распределены по ее длине. Для линий сравнительно небольшой длины распределенность параметров можно не учитывать и использовать рассредоточенные параметры: активное и реактивное сопротивление линии R и Х
и Х , и реактивную проводимости G
, и реактивную проводимости G и В
и В .
.
Воздушные линии электропередачи напряжением 110 кВ и выше длиной до 300-400 км обычно представляются П – образной схемой замещения.
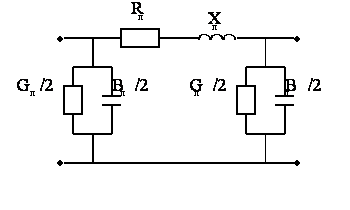
Рисунок 3.1
Активное сопротивление проводов и кабелей определяется материалом токоведущих жил и их сечениями. Погонное активное сопротивление (на 1 км длинны) для голых проводов и кабелей при температуре +20°С определяется
r =
= (3.1)
(3.1)
где r - удельное сопротивление материала проводника (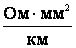 );
);
F - сечение провода, мм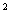 .
.
Активное сопротивление линии, длиной l определяется
R =r
=r ×l .
×l .
Активное сопротивление проводов и кабелей при частоте 50 Гц примерно равно омическому сопротивлению. При этом не учитывается влияние поверхностного эффекта. Пренебрегают также тем влиянием, которое оказывают на величину активного сопротивления колебания температуры проводника, и используют в расчетах величины этих сопротивлений при средних температурах (+20°С).
Реактивное сопротивление. Переменный ток, проходя по линии, образует вокруг проводников переменное магнитное поле, которое наводит в про-
воднике электродвижущую силу (э.д.с.) обратного направления – э.д.с. самоиндукции. При данном токе в проводе и отсутствии активного сопротивления в нем э.д.с. самоиндукции полностью уравновешивает приложенное напряжение
I×w×L=U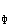
где L – коэффициент самоиндукции провода.
Сопротивление току, обусловленное противодействием э.д.с. самоиндукции, называется индуктивным сопротивлением. Соседние провода трехфазной линии, являющиеся обратными проводами для тока рассматриваемого провода, в свою очередь наводят в нем э.д.с. согласно с основным током направления, что уменьшает э.д.с. самоиндукции и соответственно реактивное сопротивление. Поэтому, чем дальше друг от друга расположены фазные провода линии, тем влияние соседних проводов будет меньше, а поток рассеяния между проводами и, следовательно, индуктивное сопротивление линии – больше.
На индуктивное сопротивление оказывают влияние также диаметр провода, магнитная проницаемость провода и частота переменного тока.
Величина погонного индуктивного сопротивления линии определяется
х = w×(4,6×lg
= w×(4,6×lg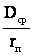 + 0,5m)×10
+ 0,5m)×10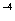 (3.2)
(3.2)
где w = 314 - угловая частота при 50 Гц;
D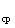 - среднегеометрическое расстояние между проводами;
- среднегеометрическое расстояние между проводами;
r - радиус провода.
- радиус провода.
Для проводов из цветного металла (μ=1) при промышленной частоте 50 Гц формула (4.2) примет вид
х = 0,144×lg
= 0,144×lg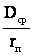 + 0,016 . (3.3)
+ 0,016 . (3.3)
Среднегеометрическое расстояние между проводами одноцепной трехфазной линии
D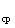 =
= 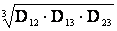
где D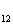 , D
, D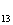 , D
, D - расстояние между проводами отдельных фаз.
- расстояние между проводами отдельных фаз.
При расположении проводов по вариантам равностороннего треугольника все провода находятся на одинаковом расстоянии относительно друг друга, и среднегеометрическое расстояние D =D (см.рисунок 3.2).
=D (см.рисунок 3.2).
При горизонтальном расположении проводов (см.рисунок 3.3).
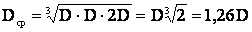

Рисунок 3.2
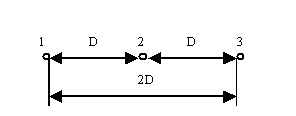
Рисунок 3.3
На линиях 330 кВ и выше применяются расщепленные провода. На таких линиях каждая фаза имеет не один, а несколько проводов. Это приводит к увеличению радиуса фазы, который определяется по выражению
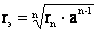 (3.4)
(3.4)
где 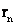 - радиус отдельных проводов, входящих в расщепленную фазу линии;
- радиус отдельных проводов, входящих в расщепленную фазу линии;
n - число проводов в одной фазе;
а - расстояние между проводами в фазе.
Индуктивное сопротивление линии с расщепленными проводами
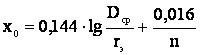 .
.
Для линии длиной l индуктивное сопротивление
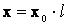 .
.
Активная проводимость линий обусловлена потерями активной мощности от токов утечки через изоляцию и от электрической короны на проводах.
Потери электрической энергии от токов утечки через изоляцию возникают при включении линии электропередачи под напряжение. Эти потери незначительны в кабельных и очень малы в воздушных линиях, значит и небольшая активная проводимость.
Потери на корону более значительны. Они связаны с ионизацией воздуха около проводов и возникают, когда напряженность электрического поля у поверхности провода превышает электрическую прочность воздуха. В этом слу-
чае на поверхности провода образуются электрические разряды. Из-за неровностей верхнего повива многопроволочных проводов, загрязнений и заусениц разряды появляются вначале только в отдельных точках провода. Это так называемая местная корона провода. По мере повышения напряжения корона распространяется на большую поверхность провода и в конечном счете охватывает провод целиком по всей его длине, т.е. возникает общая корона.
Кроме потерь электроэнергии, корона вызывает коррозию проводов, арматуры гирлянд изоляторов, оказывает мешающее воздействие на работу высокочастотных каналов связи линий электропередачи и вызывает высокочастотные помехи в проводных линиях связи и радиопомехи.
Если утечкой в линиях пренебречь, то активная проводимость, обусловленная короной определяется
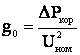 (3.5)
(3.5)
где 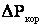 - потери мощности на корону, кВт/км;
- потери мощности на корону, кВт/км;
U - номинальное напряжение.
- номинальное напряжение.
Основными мерами по снижению потерь на корону является увеличение сечений проводов, расщепление или применение полых проводов.
Реактивная проводимость обусловлена наличием емкости между проводами и землей и имеет емкостной характер. Она определяется известным выражением.
b =w×С
=w×С
где С - рабочая емкость линии, Ф/км.
- рабочая емкость линии, Ф/км.
Рабочая емкость линии зависит от диаметра проводов, их взаимного расположения, расстояния между ними и диэлектрической проницаемости среды.
В практических расчетах электрических сетей рабочую емкость трехфазной воздушной линии с одним проводом на фазу определяют по формуле
С =
=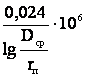 . (3.6)
. (3.6)
При частоте переменного тока 50 Гц
b =
=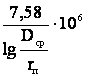 . (3.7)
. (3.7)
Емкостная проводимость всей линии
B = b ×l.
×l.
Зарядный ток линии. Под действием приложенного к линии переменного напряжения в емкости линии возникает переменное электрическое поле и возникает реактивный ток. Этот ток называется емкостным или зарядным током линии.
I×b =U
=U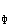 ×b
×b =
= b
b . (3.8)
. (3.8)
Зная емкостной ток линии, легко определить емкостную или зарядную мощность линии.
Qb= 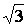 ×U×I×b
×U×I×b =
= 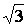 ×U×
×U×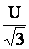 ×b
×b = U
= U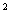 ×b
×b (3.9)
(3.9)
где U – рабочее линейное напряжение, кВ.
Кабельные линии электропередачи представляются такой же П-образной схемой замещения, что и воздушные линии. Погонные активные и реактивные сопротивления r и x
и x определяют по справочным таблицам, так же как и для воздушных. Из выражений (3.3) и (3.7) видно, что х
определяют по справочным таблицам, так же как и для воздушных. Из выражений (3.3) и (3.7) видно, что х уменьшается, b
уменьшается, b растет при сближении фазных проводов. Для кабельных линий расстояние между фазами значительно меньше, чем для воздушных и х
растет при сближении фазных проводов. Для кабельных линий расстояние между фазами значительно меньше, чем для воздушных и х очень мало. При расчетах режимов для кабельных сетей напряжением 10 кВ и ниже можно учитывать только активное сопротивление. Емкостной ток и зарядная мощность в кабельных линиях больше, чем в воздушных. В кабельных линиях высокого напряжения учитывают Q
очень мало. При расчетах режимов для кабельных сетей напряжением 10 кВ и ниже можно учитывать только активное сопротивление. Емкостной ток и зарядная мощность в кабельных линиях больше, чем в воздушных. В кабельных линиях высокого напряжения учитывают Q . Активную проводимость G учитывают для кабелей 110 кВ и выше.
. Активную проводимость G учитывают для кабелей 110 кВ и выше.
3.2 Схемы замещения, параметры трансформаторов и
автотрансформаторов
Двухобмоточные трансформаторы обычно имеют Г-образную схему замещения (см.рисунок 3.4)

Рисунок 3.4
К числу основных параметров трансформаторов относятся: потери короткого замыкания 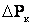 , потери холостого хода
, потери холостого хода 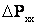 , напряжение короткого замыкания
, напряжение короткого замыкания 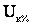 и ток холостого хода i
и ток холостого хода i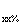 . Эти данные позволяют определить все сопротивления и проводимости схемы замещения трансформатора.
. Эти данные позволяют определить все сопротивления и проводимости схемы замещения трансформатора.
Активное и индуктивное сопротивление одной фазы трансформатора могут быть экспериментально определены из опыта короткого замыкания. Этот опыт заключается в том, что вторичная обмотка трансформатора замыкается накоротко, а к первичной обмотке подводится такое напряжение, при котором токи в обеих обмотках трансформатора имеют номинальное значение. Это напряжение называется напряжением короткого замыкания.
Активная мощность, потребляемая трансформатором в опыте короткого замыкания, практически целиком расходуется на нагрев его обмоток. Потери в стали при этом очень малы из-за маленького приложенного напряжения. Поэтому можно считать, что в опыте короткого замыкания

откуда  (3.10)
(3.10)
Напряжение короткого замыкания U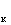 складывается из двух составляющих: падения напряжения в активном и индуктивном сопротивлениях от тока, протекающего в режиме короткого замыкания. Причем в современных крупных трансформаторах первая составляющая намного меньше, чем вторая, так как R
складывается из двух составляющих: падения напряжения в активном и индуктивном сопротивлениях от тока, протекающего в режиме короткого замыкания. Причем в современных крупных трансформаторах первая составляющая намного меньше, чем вторая, так как R <<Х
<<Х . Пренебрегая падением напряжения в активном сопротивлении трансформатора, можно считать
. Пренебрегая падением напряжения в активном сопротивлении трансформатора, можно считать
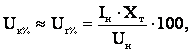 (3.11)
(3.11)
откуда
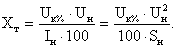 (3.12)
(3.12)
Проводимости G и B
и B схемы замещения трансформатора определяются по результатам опыта холостого хода, в котором при разомкнутой вторичной обмотке к первичной обмотке подводится номинальное напряжение. Как следует из схемы замещения трансформатора, ток и соответствующая мощность, потребляемая трансформатором в этом режиме, определяются параметрами цепи намагничивания. Следовательно,
схемы замещения трансформатора определяются по результатам опыта холостого хода, в котором при разомкнутой вторичной обмотке к первичной обмотке подводится номинальное напряжение. Как следует из схемы замещения трансформатора, ток и соответствующая мощность, потребляемая трансформатором в этом режиме, определяются параметрами цепи намагничивания. Следовательно,


откуда 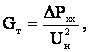 (3.13)
(3.13)
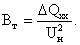 (3.14)
(3.14)
Намагничивающая мощность 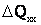 обычно принимается равной полной мощности холостого хода трансформатора S
обычно принимается равной полной мощности холостого хода трансформатора S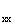 ввиду малости потерь активной мощности DР
ввиду малости потерь активной мощности DР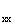 в сравнении с DQ
в сравнении с DQ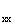 .
.
Мощность S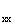 в относительных единицах равна току холостого хода в процентах, который указывается в паспортных данных трансформаторов
в относительных единицах равна току холостого хода в процентах, который указывается в паспортных данных трансформаторов
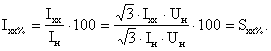
Трехобмоточные трансформаторы представляются схемой замещения в виде трехлучевой звезды (см.рисунок 3.5)
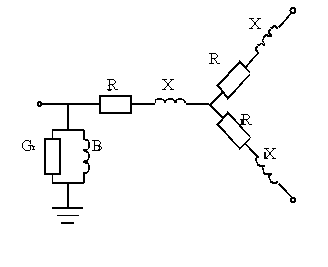
Рисунок 3.5
Современные трехобмоточные трансформаторы выполняются с соотношением мощностей обмоток 100/100/100%, т.е. каждая из обмоток расчитана на передачу всей мощности.
Активные сопротивления лучей звезды в схеме замещения трехобмоточного трансформатора определяют по общему сопротивлению трансформатора.
При равенстве мощностей обмоток
R =R
=R =R
=R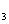 =0,5R
=0,5R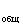 .
.
Общее сопротивление трансформатора R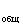 определяют по формуле (3.10), в которую подставляют DР
определяют по формуле (3.10), в которую подставляют DР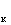 максимальные потери мощности короткого замыкания при номинальной нагрузке обмотки НН, обозначенные в паспортных данных трансформатора.
максимальные потери мощности короткого замыкания при номинальной нагрузке обмотки НН, обозначенные в паспортных данных трансформатора.
Для трехобмоточных трансформаторов напряжения короткого замыкания даются заводами для каждой пары обмоток в процентах от номинального U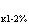 , U
, U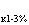 , U
, U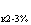 .
.
Согласно эквивалентной схеме замещения лучей трансформатора при одной из обмоток, остающейся разомкнутой, можно записать
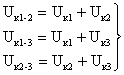 (3.15)
(3.15)
Решив совместно эти уравнения относительно U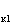 , U
, U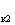 ,U
,U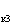 , найдем
, найдем
 (3.16)
(3.16)
Подставив эти значения в выражение (3.12), получим индуктивное сопротивление каждой обмотки трансформатора.
Проводимости не зависят от числа обмоток в трансформаторе и определяются так же как и для двухобмоточного.
Трансформаторы с расщепленными обмотками. Для того чтобы сделать возможным присоединение к одному трансформатору двух и более генераторов или независимых нагрузок одного или разных (соседних классов) напряжений на приемных подстанциях, современные трансформаторы высокого напряжения изготавливаются с обмотками низкого напряжения, расщепленными на две (или более) ветви.
Применение трансформаторов с расщепленными обмотками для раздельного питания секций распределительного устройства от обмоток НН позволит снизить мощность короткого замыкания на шинах секций почти в два раза без установки сдвоенных токоограниченных реакторов.
Автотрансформаторы так же, как и трансформаторы характеризуются номинальными напряжениями и номинальной мощностью. Под номинальной мощностью автотрансформатора понимается предельная мощность, которая может быть передана через автотрансформатор на стороне высшего напряжения
S =
=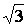 ×I
×I ×U
×U .
.
На рисунке 3.6 приведена схема соединения обмоток одной фазы автотрансформатора

Рисунок 3.6
Из схемы видно, что часть обмотки высшего напряжения ВСО, заключенная между точками С и О, является обмоткой среднего напряжения U и называется общей обмоткой, а другая ее часть ВС – последовательной обмоткой. Таким образом, у автотрансформаторов обмотка среднего напряжения является частью обмотки высшего напряжения, т.е. эти обмотки связаны между собой электрически, а обмотка низшего напряжения U
и называется общей обмоткой, а другая ее часть ВС – последовательной обмоткой. Таким образом, у автотрансформаторов обмотка среднего напряжения является частью обмотки высшего напряжения, т.е. эти обмотки связаны между собой электрически, а обмотка низшего напряжения U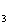 имеет магнитную связь с ними.
имеет магнитную связь с ними.
Для характеристики автотрансформаторов введено понятие типовой мощности, на которую рассчитывается последовательная обмотка.
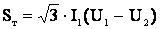 . (3.17)
. (3.17)
Умножим и разделим это выражение на U , получим
, получим
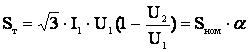 (3.18)
(3.18)
где a=1 - 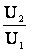 - коэффициент выгодности автотрансформатора.
- коэффициент выгодности автотрансформатора.
В понижающем автотрансформаторе ток в общей обмотке равен разности токов обмоток высшего и среднего напряжений, т.е.
I =I
=I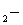 I
I .
.
Поэтому эта обмотка рассчитывается на ток, меньший номинального тока автотрансформатора, протекающего на высшей обмотке. Расчетная мощность этой обмотки меньше номинальной мощности автотрансформатора и равна его типовой мощности. Обмотка низшего напряжения рассчитывается также на передачу типовой мощности.
Таким образом, конструкция автотрансформаторов делает возможной передачу через автотрансформатор мощности больше той, на которую рассчи-
тываются его обмотки. Благодаря этому, понижающие автотрансформаторы оказываются дешевле трехобмоточных трансформаторов равной номинальной мощности, характеризуются меньшим расходом активных материалов на их изготовление и, как следствие, меньшими потерями активной мощности.
Схема замещения автотрансформатора так же как и у трехобмоточного в виде трехлучевой звезды. При соотношении мощностей обмоток автотрансформатора 100/100/50% активные сопротивления лучей определяются
R =R
=R , R
, R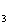 =2R
=2R =2R
=2R .
.
Индуктивные сопротивления определяются так же, как и для трехобмоточных трансформаторов.
3.3 Определение потерь мощности и энергии в линиях
При передаче электрической энергии во всех звеньях электрических сетей имеются потери активной мощности и энергии. Эти потери возникают как в воздушных и кабельных линиях, так и в трансформаторах понижающих и повышающих подстанций.
Потери активной мощности на участке трехфазной линии с активным сопротивлением R составляют
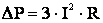 (3.19)
(3.19)
где I – ток нагрузки.
Если выразить ток через мощность, то получим
I=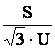 .
.
Подставим значение тока в (3.19), получим
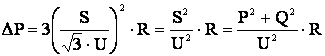 . (3.20)
. (3.20)
Аналогично получим потери реактивной мощности
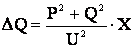 . (3.21)
. (3.21)
Потери активной энергии в сети можно определить, умножив потери активной мощности на время работы сети с данной нагрузкой. Однако нагрузка потребителей колеблется в течение суток и времени года, поэтому изменяется и размер величины потерь мощности.
Таким образом, определение потерь энергии для каждой линии должно быть произведено путем суммирования (интегрирования) значений потерь мощности за бесконечно малые элементы времени, т.е.
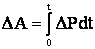 ,
,
или, подставляя значение DР из формулы (6.2), получаем
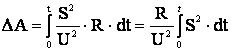
где S – полная мощность, передаваемая по линии и представляющая собой функцию от времени t.

Рисунок 3.7 - Годовой график нагрузки по продолжительности.

Рисунок 3.8 - Ступенчатый график нагрузки по продолжительности.
Эту функцию обычно изображают в виде графика по продолжительности (см.рисунок 3.8). Этот график показывает продолжительность работы сети с данной нагрузкой (кривая 1). При неизменном коэффициенте мощности нагрузки площадь, ограниченная этой кривой, показывает в некотором масштабе количество энергии, передаваемое по сети в течение года и выражается формулой
А=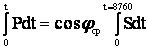
где cos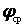 - средний коэффициент мощности, принимаемый приближенно постоянным в течение года.
- средний коэффициент мощности, принимаемый приближенно постоянным в течение года.
Если кривую 1 графика (см.рисунок 3.7) перестроить в квадратичную кривую 2, выражающую функцию S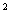 =f(t), то потери легко определяются в некотором масштабе по площади, ограниченной этой кривой
=f(t), то потери легко определяются в некотором масштабе по площади, ограниченной этой кривой
DА=
Из этого следует, что для определения потерь электроэнергии достаточно измерить площадь, ограниченную кривой 2. Практически это можно сделать приближенно, заменив график нагрузки по продолжительности ступенчатым графиком с достаточно малыми отрезками времени t , t
, t , … t
, … t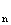 и соответствующими значениями нагрузок S
и соответствующими значениями нагрузок S , S
, S , … S
, … S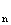 (см.рисунок 3.8). Тогда потери энергии определяются суммированием величин
(см.рисунок 3.8). Тогда потери энергии определяются суммированием величин
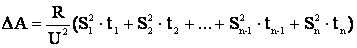 . (3.22)
. (3.22)
В это выражение можно ввести величину
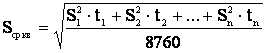 ,
,
тогда
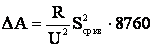 . (3.23)
. (3.23)
Величина S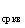 носит название среднеквадратичной мощности, а метод определения потерь мощности по формуле (3.23) называется методом определения потерь по среднеквадратичной мощности.
носит название среднеквадратичной мощности, а метод определения потерь мощности по формуле (3.23) называется методом определения потерь по среднеквадратичной мощности.
Этот метод приближенного определения потерь обладает рядом неудобств и применим только при наличии графика нагрузки. Поэтому более распространен так называемый метод определения потерь по времени максимальных потерь, который значительно упрощает расчеты.
Для годового графика нагрузки по продолжительности (кривая 1- рисунок 3.7) можно найти такое время Т, в течение которого по линии, работающей
с максимальной нагрузкой S , передавалось бы такое же количество энергии, какое передается по ней в действительности в течение года при изменяющейся нагрузке S=f(t).
, передавалось бы такое же количество энергии, какое передается по ней в действительности в течение года при изменяющейся нагрузке S=f(t).
При неизменном коэффициенте мощности это условие может быть записано следующим образом
 , (3.24)
, (3.24)
отсюда
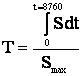 . (3.25)
. (3.25)
Величина Т называется временем использования максимальной нагрузки.
Зная годовое количество энергии А, передаваемое по линии, и максимальную активную нагрузку Р , из формулы (3.24) можно определить время использования максимальной нагрузки
, из формулы (3.24) можно определить время использования максимальной нагрузки
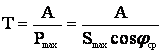 . (3.26)
. (3.26)
Для каждого потребителя характерна своя величина времени использования максимальной нагрузки. При расчетах эту величину принимают на основании статистических и справочных данных.
Величину времени использования максимальной нагрузки надо знать, чтобы определять потери электроэнергии. Для этого пользуются величиной t - временем максимальных потерь, т.е. временем, в течение которого линия, работая с неизменной максимальной нагрузкой, имеет потери электроэнергии, равные действительным годовым потерям электроэнергии при работе по годовому графику нагрузки. Заменяя площадь, ограниченную кривой 2 (см.рисунок 3.7), площадью прямоугольника со сторонами t и S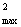 , получаем
, получаем
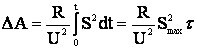 . (3.27)
. (3.27)
Отсюда получаем время максимальных потерь
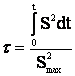 . (3.28)
. (3.28)
Практически величину t получают из времени Т, так как между ними существует определенная зависимость.
Как видно из формул (3.25) и (3.28), t и Т зависят от характера изменения графика нагрузки, т.е. от функции S=f(t), находящейся в этих формулах
под знаком интеграла. Для нахождения зависимости t от Т можно проинтегри-
ровать ряд графиков нагрузки, имеющих различные величины Т для различных потребителей, и то же сделать с квадратичными кривыми S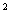 = f(t) этих же графиков, и затем, пользуясь формулами (3.25) и (3.28), установить зависимости t и Т для различных значений cosj. Результаты расчетов представлены на рисунке 3.9 в виде семейства кривых. Этими кривыми можно пользоваться для определения потерь энергии методом времени максимальных потерь.
= f(t) этих же графиков, и затем, пользуясь формулами (3.25) и (3.28), установить зависимости t и Т для различных значений cosj. Результаты расчетов представлены на рисунке 3.9 в виде семейства кривых. Этими кривыми можно пользоваться для определения потерь энергии методом времени максимальных потерь.

Рисунок 3.9
Порядок расчета следующий. Зная активное сопротивление рассматриваемой линии R, максимальную нагрузку S , cosj
, cosj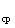 и время использования максимальной нагрузки для данной категории потребителей по кривой (см.рисунок 3.9) для заданного cosj
и время использования максимальной нагрузки для данной категории потребителей по кривой (см.рисунок 3.9) для заданного cosj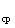 и известного Т, находим время максимальных потерь t. Далее определяем потери электроэнергии.
и известного Т, находим время максимальных потерь t. Далее определяем потери электроэнергии.
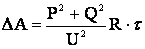 . (3.29)
. (3.29)
Если по рассматриваемому участку линии передается мощность к различным потребителям Р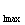 , Р
, Р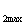 ,Р
,Р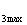 и т.д., то при определении потерь следует принимать среднюю величину времени использования максимальной нагрузки, определяемую с учетом суммарной величины передаваемой энергии.
и т.д., то при определении потерь следует принимать среднюю величину времени использования максимальной нагрузки, определяемую с учетом суммарной величины передаваемой энергии.
 . (3.30)
. (3.30)
Для графиков пиковой формы величина t определяется по эмпирической формуле
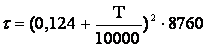 . (3.31)
. (3.31)
3.4 Потери мощности и энергии в трансформаторах
Потери мощности через трансформатор всегда связаны с потерями мощности в активном и реактивном сопротивлениях его обмоток и потерями, связанными с намагничиванием стали. Потери, возникающие в обмотках, зависят от протекающего по ним тока. Потери, идущие на намагничивание, определяются приложенным напряжением и могут быть приняты неизменными и равными потерям холостого хода.
В двухобмоточных трансформаторах потери мощности определяются как
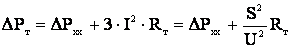 , (3.32)
, (3.32)
 . (3.33)
. (3.33)
В тех случаях, когда напряжение U неизвестно, принимают его равным номинальному напряжению трансформатора, к которому приведены его сопротивления R и X
и X .
.
При параллельной работе n одинаковых трансформаторов их эквивалентное сопротивление уменьшается в n раз, а потери на намагничивание увеличиваются в n раз.
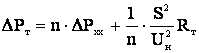 , (3.34)
, (3.34)
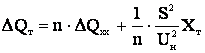 . (3.35)
. (3.35)
Потери мощности могут быть найдены непосредственно по каталожным параметрам трансформаторов без предварительного вычисления сопротивлений r и х
и х . Поскольку потери короткого замыкания
. Поскольку потери короткого замыкания  определяются при номинальном токе трансформатора
определяются при номинальном токе трансформатора
 =3
=3 ,
,
а при любом другом токе, потери активной мощности в обмотках
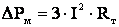 ,
,
то справедлива зависимость
 .
.
Значит при одном трансформаторе
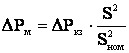 , (3.36)
, (3.36)
а при параллельной работе n одинаковых трансформаторов
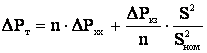 . (3.37)
. (3.37)
Подставив значение реактивного сопротивления (3.12) в (3.35), получим
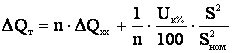 . (3.38)
. (3.38)
Из (3.38) следует, что при S=S напряжение короткого замыкания U
напряжение короткого замыкания U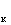 численно равно потере реактивной мощности в обмотках трансформатора, выраженной в долях от его номинальной мощности.
численно равно потере реактивной мощности в обмотках трансформатора, выраженной в долях от его номинальной мощности.
В трехобмоточных трансформаторах и автотрансформаторах потери активной мощности определяются суммированием потерь мощности в каждой из обмоток
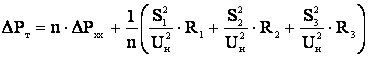 (3.39)
(3.39)
где S , S
, S , S
, S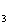 - соответственно мощности, протекающие по обмоткам высшего, среднего и низшего напряжений.
- соответственно мощности, протекающие по обмоткам высшего, среднего и низшего напряжений.
Потери реактивной мощности определяются
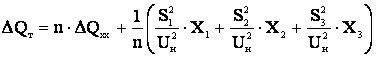 . (3.40)
. (3.40)
Потери энергии в трансформаторах определяют следующим образом:
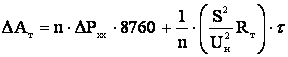 . (3.41)
. (3.41)
для трехобмоточных и автотрансформаторов
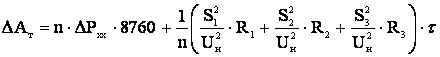 . (3.42)
. (3.42)
4 Расчет рабочих режимов разомкнутых и простых замкнутых электрических сетей
4.1 Задача расчета режима сети, основные допущения
Основную задачу расчета режима сети составляет определение параметров режима. Как уже указывалось, к таким параметрам относятся: токи на участках сети, активные и реактивные мощности, напряжение в узлах сети, частота и др.
Исходными данными для расчета служат: расчетные мощности нагрузок, заданные величины напряжения в отдельных точках, схема электрических соединений сети, характеризующая взаимную связь ее элементов и другие величины.
Основным методом для электрического расчета сети является метод последовательных приближений (итераций), который предусматривает постепенный переход от более грубых ответов на поставленную задачу к более точным решениям. Первое приближение (нулевая итерация) при этом может быть получено на основании тех или иных представлений о возможных значениях искомых величин. Применительно к электрическим сетям в качестве первого приближения принимают равенство напряжений во всех точках сети номинальному напряжению. Это позволяет определить токи нагрузок и остальные параметры режима сети, в том числе и напряжения на зажимах нагрузки. Найденные напряжения являются уже вторым приближением к истинному решению. На основании этого можно снова найти токи и продолжать выполнять расчеты до тех пор, пока результаты последующих приближений не будут с заданной точностью отличаться от результатов предыдущих.
Практически при проведении расчетов электрических сетей можно ограничится второй и первой итерациями. К числу таких расчетов относятся расчеты сетей 35 кВ и ниже, а в ряде случаев – проектные расчеты сетей напряжением 110 и 220 кВ. При анализе режимов сетей 35 кВ и ниже ограничиваются первым приближением. Связано это с тем, что требования потребителей к качеству напряжения определяет необходимость обеспечивать для всех точек таких сетей напряжения, мало отличающихся от номинальных, которые принимаются при расчетах первого приближения. Получаемая при этом ошибка лежит в пределах точности расчета. Ошибка, получаемая при ограничении расчетов сетей 110 и 220 кВ вторым приближением, также оказывается в пределах точности расчета.
4.2 Расчет линии с нагрузкой на конце по потере напряжения
Рассмотрим простейшую линию трехфазного тока с симметричной нагрузкой на конце (см.рисунок 4.1).

Рисунок 4.1
Нагрузка задана либо током I и cosj при фазном напряжении U на конце линии, либо мощностью S = P + jQ.
на конце линии, либо мощностью S = P + jQ.
Расчет проводится с помощью векторной диаграммы токов и напряжений для одной фазы линии, что допускается, так как нагрузка во всех фазах симметрична.
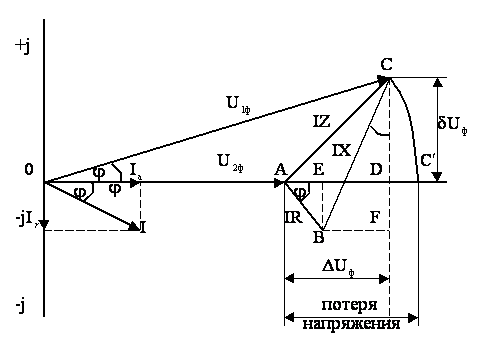
Рисунок 4.2 - Векторная диаграмма линии с нагрузкой на конце
Известны ток нагрузки I, cosj и напряжение U . Необходимо определить U
. Необходимо определить U . По действительной оси откладываем вектор заданного напряжения в конце линии U
. По действительной оси откладываем вектор заданного напряжения в конце линии U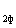 (ОА). Из начала координат откладываем вектор тока I под углом j. Его активная составляющая направлена по действительной оси I
(ОА). Из начала координат откладываем вектор тока I под углом j. Его активная составляющая направлена по действительной оси I , а реактивная составляющая -jI
, а реактивная составляющая -jI - по мнимой оси в отрицательном направлении. Таким образом, при принятом расположении вектора напряжения и тока на векторной диаграмме знак минус у мнимой части комплекса тока характеризует индуктивный (отстающий) ток нагрузки потребителя.
- по мнимой оси в отрицательном направлении. Таким образом, при принятом расположении вектора напряжения и тока на векторной диаграмме знак минус у мнимой части комплекса тока характеризует индуктивный (отстающий) ток нагрузки потребителя.
Далее из точки А откладываем параллельно вектору тока I вектор падения напряжения в активном сопротивлении линии IR (АВ) и под углом 90 к нему в сторону опережения – вектор падения напряжения в реактивном сопротивлении IX (ВС). Соединив точку А с точкой С, получим вектор полного па-
к нему в сторону опережения – вектор падения напряжения в реактивном сопротивлении IX (ВС). Соединив точку А с точкой С, получим вектор полного па-
дения напряжения в рассматриваемой линии IZ (АС). Чтобы найти напряжение U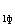 , соединим точку С с началом координат, получаем вектор фазного напряжения в начале линии U
, соединим точку С с началом координат, получаем вектор фазного напряжения в начале линии U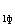 (ОС).
(ОС).
Падение напряжения в линии
IZ = 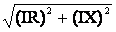
может быть разложено на составляющие:
а) продольную DU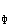 = АD
= АD
б) поперечную d U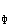 = DC
= DC
т.е. IZ = DU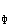 + jd U
+ jd U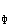 .
.
Определим эти составляющие. Для этого опустим перпендикуляры из точек В и С на действительную и мнимую оси. В результате получим отрезки:
АЕ = IRcosj; ED = BF = IXsinj;
CF = IXcosj; BE = DF = IRsinj.
Отсюда продольная составляющая
DU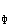 = AD = AE + ED = IRcosj + IXsinj = I
= AD = AE + ED = IRcosj + IXsinj = I R + I
R + I X, (4.1)
X, (4.1)
d U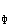 = DC = CF - DF = IXcosj - IRsinj = I
= DC = CF - DF = IXcosj - IRsinj = I X + I
X + I R. (4.2)
R. (4.2)
Напряжение в начале линии
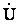
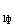 = U
= U + DU
+ DU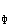 + jdU
+ jdU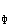 ,
,
а модуль напряжения
U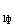 =
= 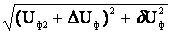 . (4.3)
. (4.3)
В результате построения диаграммы выше был получен вектор полного падения напряжения в линии. Следует отметить, что под падением напряжения понимают геометрическую разность потенциалов между началом и концом линии.
При расчете сетей 35 кВ и ниже обычно вводятся упрощения, заключающиеся в том, что напряжение в начале линии определяют не по падению напряжения, а по потере напряжения. Под потерей напряжения понимают алгебраическую разность абсолютных значений напряжений в начале и в конце линии.
Для определения потери напряжения на диаграмме совместим отрезок ОС с осью действительных величин (отрезок О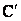 ).
).
Отрезок А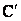 = О
= О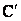 - ОА = U
- ОА = U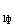 - U
- U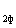 представляет собой потерю напряжения.
представляет собой потерю напряжения.
Так как для сетей 35 кВ и ниже углы между U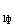 и U
и U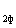 очень малы, а значит мал и отрезок D
очень малы, а значит мал и отрезок D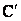 , то можно считать, что потеря напряжения приблизительно равна продольной составляющей падения напряжения
, то можно считать, что потеря напряжения приблизительно равна продольной составляющей падения напряжения
АD » A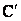 » DU
» DU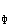 » IRcosj + IXsinj . (4.4)
» IRcosj + IXsinj . (4.4)
Потеря линейного напряжения
DU = 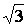 DU
DU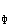 =
= 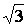 I(Rcosj + Xsinj) . (4.5)
I(Rcosj + Xsinj) . (4.5)
Векторная диаграмма линейных напряжений будет выглядеть аналогично диаграмме фазных напряжений.
При задании нагрузки активной и реактивной мощностью Р+jQ величина потери напряжения определяется следующим образом
Так как I = Icosj =
= Icosj = 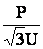 и I
и I = Isinj =
= Isinj = 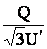 , то, подставив эти значения в (4.5), получим
, то, подставив эти значения в (4.5), получим
DU = 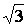 (IRcosj + IXsinj) =
(IRcosj + IXsinj) = 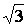
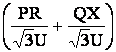 ,
,
или
DU = 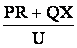 . (4.6)
. (4.6)
Часто при расчетах напряжение у потребителей бывает неизвестно, то вместо действительного в конце линии можно принимать номинальное напряжение
DU = 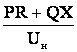 . (4.7)
. (4.7)
При расчетах сети с несколькими нагрузками величина потери напряжения определяется как сумма потерь напряжений на всех участках сети
DU = 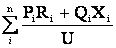 . (4.8)
. (4.8)
4.3 Расчеты режима разомкнутых электрических сетей
При расчете режима сетей 110 – 220 кВ можно выделить два характерных расчетных случая: расчет сети по заданному напряжению в конце линии (или расчет по данным конца) и расчет, в котором заданным является напряжение в начале линии (расчет по данным начала).
На рисунке 4.3 представлена расчетная схема разомкнутой сети с n нагрузками (а) и ее схема замещения (б).

Рисунок 4.3
Рассмотрим случай расчета по данным конца. Исходными данными являются: напряжение в конце линии U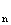 , расчетные мощности нагрузок, а также параметры сети. Расчет ведется от конца линии. По известному напряжению U
, расчетные мощности нагрузок, а также параметры сети. Расчет ведется от конца линии. По известному напряжению U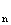 определяются потери мощности на последнем участке линии n
определяются потери мощности на последнем участке линии n
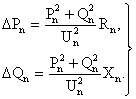 (4.9)
(4.9)
Находим мощность в начале участка n
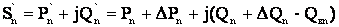 (4.10)
(4.10)
где Q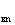 - зарядная мощность на участке n.
- зарядная мощность на участке n.
Мощность в конце участка (n-1) по балансу мощности в узле (n-1) определяется
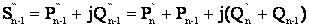 . (4.11)
. (4.11)
Падение напряжения на концевом участке n определяется
D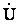
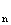 = DU
= DU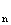 + jdU
+ jdU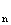 =
=  + j
+ j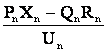 . (4.12)
. (4.12)
По известному напряжению U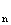 и падению напряжения на участке n определяется напряжение в узле n-1 U
и падению напряжения на участке n определяется напряжение в узле n-1 U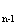
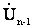 =
= 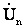 + D
+ D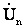 = U
= U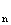 + DU
+ DU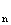 + jdU
+ jdU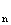 (4.13)
(4.13)
или модуль напряжения
U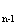 =
=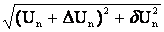 . (4.14)
. (4.14)
Определением напряжения 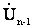 закачивается расчет режима концевого участка сети. При этом оказываются известными все необходимые данные для расчета следующего участка. Расчет участка n-1 выполняется по тем же формулам, что и для участка n. Аналогично ведутся расчеты для всех остальных участков. Окончанием расчета является определение мощности
закачивается расчет режима концевого участка сети. При этом оказываются известными все необходимые данные для расчета следующего участка. Расчет участка n-1 выполняется по тем же формулам, что и для участка n. Аналогично ведутся расчеты для всех остальных участков. Окончанием расчета является определение мощности 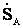 и напряжения
и напряжения 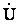
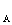 .
.
В расчетах сети по данным начала, в которых известной величиной является напряжение в точке питания 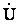
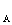 , используется метод последовательных приближений, причем расчеты выполняются в два этапа.
, используется метод последовательных приближений, причем расчеты выполняются в два этапа.
В качестве первого приближения (на первом этапе расчета) принимается, что напряжения во всех узлах равны номинальному напряжению сети. При этом условии находится распределение мощностей в сети.
В соответствии с обозначениями на рисунке 4.3 расчет ведется в следующей последовательности. Определяются потери мощности на концевом участке сети
DP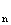 =
=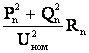 ,
,
(4.15)
DQ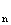 =
=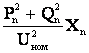 .
.
Далее определяется мощность 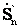 в начале этого участка в соответствии с (4.10). По балансу мощности в узле (n-1) определяется мощность в конце участка n-1 по (4.11). Аналогично ведется расчет и для всех остальных участков сети. Расчет продолжается до тех пор, пока не определится
в начале этого участка в соответствии с (4.10). По балансу мощности в узле (n-1) определяется мощность в конце участка n-1 по (4.11). Аналогично ведется расчет и для всех остальных участков сети. Расчет продолжается до тех пор, пока не определится 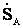 .
.
На следующем этапе расчета определяются напряжения в узлах нагрузки во втором приближении. Исходными данными для расчета являются: напряжение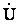
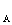 и найденные в предыдущем этапе расчета мощности в конце каждого из участков. Для головного участка сети
и найденные в предыдущем этапе расчета мощности в конце каждого из участков. Для головного участка сети
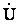
 =
= 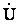
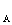 - D
- D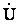
 , (4.16)
, (4.16)
где D
 - падение напряжения на головном участке сети.
- падение напряжения на головном участке сети.
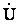
 =
= 
| <== попередня лекція |
| |
наступна лекція ==> |
| Опоры ВЛ. | | | Первичное регулирование частоты. |







 и Х
и Х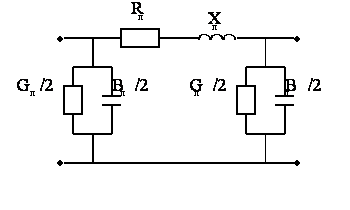
 =
= (3.1)
(3.1)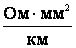 );
);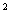 .
. =r
=r ×l .
×l .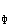
 + 0,5m)×10
+ 0,5m)×10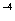 (3.2)
(3.2)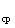 - среднегеометрическое расстояние между проводами;
- среднегеометрическое расстояние между проводами; - радиус провода.
- радиус провода.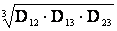
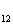 , D
, D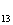 , D
, D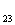 - расстояние между проводами отдельных фаз.
- расстояние между проводами отдельных фаз.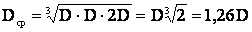

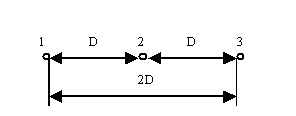
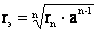 (3.4)
(3.4)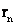 - радиус отдельных проводов, входящих в расщепленную фазу линии;
- радиус отдельных проводов, входящих в расщепленную фазу линии;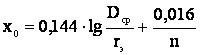 .
.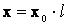 .
.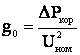 (3.5)
(3.5)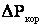 - потери мощности на корону, кВт/км;
- потери мощности на корону, кВт/км; - номинальное напряжение.
- номинальное напряжение.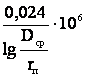 . (3.6)
. (3.6)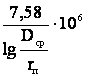 . (3.7)
. (3.7) b
b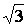 ×U×I×b
×U×I×b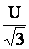 ×b
×b . Активную проводимость G учитывают для кабелей 110 кВ и выше.
. Активную проводимость G учитывают для кабелей 110 кВ и выше.
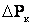 , потери холостого хода
, потери холостого хода 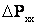 , напряжение короткого замыкания
, напряжение короткого замыкания 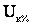 и ток холостого хода i
и ток холостого хода i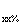 . Эти данные позволяют определить все сопротивления и проводимости схемы замещения трансформатора.
. Эти данные позволяют определить все сопротивления и проводимости схемы замещения трансформатора.
 (3.10)
(3.10)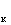 складывается из двух составляющих: падения напряжения в активном и индуктивном сопротивлениях от тока, протекающего в режиме короткого замыкания. Причем в современных крупных трансформаторах первая составляющая намного меньше, чем вторая, так как R
складывается из двух составляющих: падения напряжения в активном и индуктивном сопротивлениях от тока, протекающего в режиме короткого замыкания. Причем в современных крупных трансформаторах первая составляющая намного меньше, чем вторая, так как R <<Х
<<Х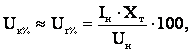 (3.11)
(3.11)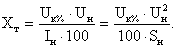 (3.12)
(3.12)

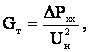 (3.13)
(3.13)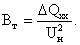 (3.14)
(3.14)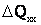 обычно принимается равной полной мощности холостого хода трансформатора S
обычно принимается равной полной мощности холостого хода трансформатора S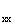 ввиду малости потерь активной мощности DР
ввиду малости потерь активной мощности DР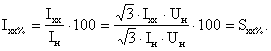
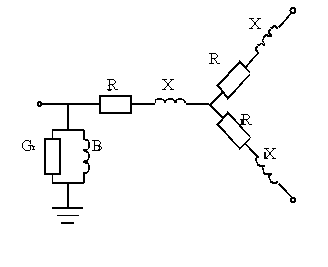
 =R
=R =R
=R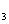 =0,5R
=0,5R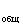 .
.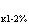 , U
, U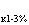 , U
, U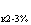 .
.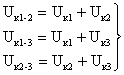 (3.15)
(3.15)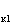 , U
, U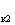 ,U
,U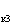 , найдем
, найдем (3.16)
(3.16)
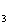 имеет магнитную связь с ними.
имеет магнитную связь с ними.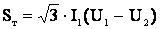 . (3.17)
. (3.17)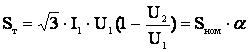 (3.18)
(3.18)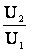 - коэффициент выгодности автотрансформатора.
- коэффициент выгодности автотрансформатора.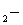 I
I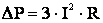 (3.19)
(3.19)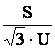 .
.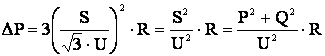 . (3.20)
. (3.20)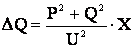 . (3.21)
. (3.21)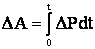 ,
,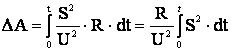


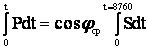
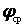 - средний коэффициент мощности, принимаемый приближенно постоянным в течение года.
- средний коэффициент мощности, принимаемый приближенно постоянным в течение года.
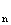 и соответствующими значениями нагрузок S
и соответствующими значениями нагрузок S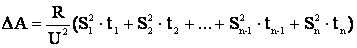 . (3.22)
. (3.22)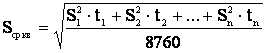 ,
,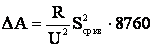 . (3.23)
. (3.23)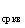 носит название среднеквадратичной мощности, а метод определения потерь мощности по формуле (3.23) называется методом определения потерь по среднеквадратичной мощности.
носит название среднеквадратичной мощности, а метод определения потерь мощности по формуле (3.23) называется методом определения потерь по среднеквадратичной мощности. , передавалось бы такое же количество энергии, какое передается по ней в действительности в течение года при изменяющейся нагрузке S=f(t).
, передавалось бы такое же количество энергии, какое передается по ней в действительности в течение года при изменяющейся нагрузке S=f(t). , (3.24)
, (3.24)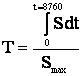 . (3.25)
. (3.25)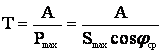 . (3.26)
. (3.26)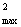 , получаем
, получаем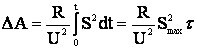 . (3.27)
. (3.27)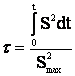 . (3.28)
. (3.28)
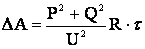 . (3.29)
. (3.29)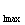 , Р
, Р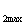 ,Р
,Р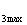 и т.д., то при определении потерь следует принимать среднюю величину времени использования максимальной нагрузки, определяемую с учетом суммарной величины передаваемой энергии.
и т.д., то при определении потерь следует принимать среднюю величину времени использования максимальной нагрузки, определяемую с учетом суммарной величины передаваемой энергии. . (3.30)
. (3.30)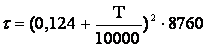 . (3.31)
. (3.31)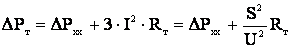 , (3.32)
, (3.32) . (3.33)
. (3.33)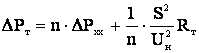 , (3.34)
, (3.34)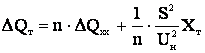 . (3.35)
. (3.35) определяются при номинальном токе трансформатора
определяются при номинальном токе трансформатора ,
,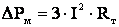 ,
, .
.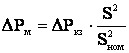 , (3.36)
, (3.36)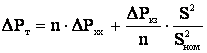 . (3.37)
. (3.37)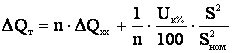 . (3.38)
. (3.38)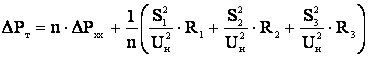 (3.39)
(3.39)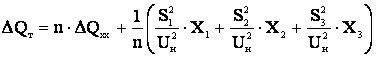 . (3.40)
. (3.40)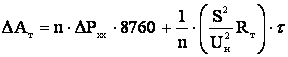 . (3.41)
. (3.41)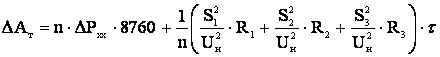 . (3.42)
. (3.42)
 на конце линии, либо мощностью S = P + jQ.
на конце линии, либо мощностью S = P + jQ.
 . По действительной оси откладываем вектор заданного напряжения в конце линии U
. По действительной оси откладываем вектор заданного напряжения в конце линии U , а реактивная составляющая -jI
, а реактивная составляющая -jI - по мнимой оси в отрицательном направлении. Таким образом, при принятом расположении вектора напряжения и тока на векторной диаграмме знак минус у мнимой части комплекса тока характеризует индуктивный (отстающий) ток нагрузки потребителя.
- по мнимой оси в отрицательном направлении. Таким образом, при принятом расположении вектора напряжения и тока на векторной диаграмме знак минус у мнимой части комплекса тока характеризует индуктивный (отстающий) ток нагрузки потребителя. к нему в сторону опережения – вектор падения напряжения в реактивном сопротивлении IX (ВС). Соединив точку А с точкой С, получим вектор полного па-
к нему в сторону опережения – вектор падения напряжения в реактивном сопротивлении IX (ВС). Соединив точку А с точкой С, получим вектор полного па-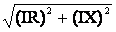
 X, (4.1)
X, (4.1)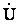
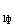 = U
= U + DU
+ DU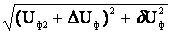 . (4.3)
. (4.3)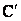 ).
).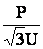 и I
и I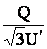 , то, подставив эти значения в (4.5), получим
, то, подставив эти значения в (4.5), получим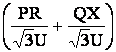 ,
,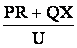 . (4.6)
. (4.6)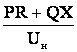 . (4.7)
. (4.7)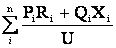 . (4.8)
. (4.8)
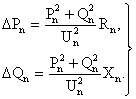 (4.9)
(4.9)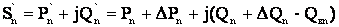 (4.10)
(4.10)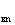 - зарядная мощность на участке n.
- зарядная мощность на участке n.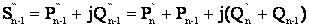 . (4.11)
. (4.11) + j
+ j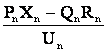 . (4.12)
. (4.12)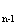
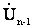 =
= 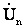 + D
+ D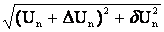 . (4.14)
. (4.14)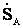 и напряжения
и напряжения 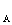 .
.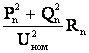 ,
,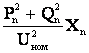 .
. в начале этого участка в соответствии с (4.10). По балансу мощности в узле (n-1) определяется мощность в конце участка n-1 по (4.11). Аналогично ведется расчет и для всех остальных участков сети. Расчет продолжается до тех пор, пока не определится
в начале этого участка в соответствии с (4.10). По балансу мощности в узле (n-1) определяется мощность в конце участка n-1 по (4.11). Аналогично ведется расчет и для всех остальных участков сети. Расчет продолжается до тех пор, пока не определится