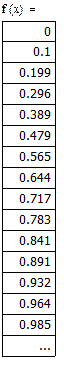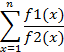Завдання № 1: Скласти схему алгоритму и програму по ньому для обчислення суми членів ряда:
n
S = å F1 / F2
i=1
Варіанти індивідуальних завдань вказані в таб.3, номер варіанту співпадає з Вашим номером у журналі
Завдання № 2: Скласти схему алгоритму и програму по ньому для визначення значень функції y = F(x) на відрізку [A,B] з кроком H.
Варіанти індивідуальних завдань вказані в таб.4, номер варіанту співпадає з Вашим номером у журналі.
ХІД РОБОТИ:
1. Скласти схему алгоритму и програму для завдання згідно вашого варіанту
2. Увійдіть у систему програмування Borland Pascal 7.0– для цього необхідно два рази щелкнути мишою на позначки програми, яка знаходиться на Робочому столі Windows.
3. В системі вийти в меню Borland Pascal 7.0 за допомогою миши, вибрати пункт File, війти в нього и обрати одну з команд: New – якщо необхідно вводити нову програму, Open –якщо бажаєте визвати раніше створену програму ( для цього необхідно або ввести ім’я файлу, або вийти у список файлів (клавіша [Tab]) и з допомогою клавіш управління курсором вибрати необхідний файл и нажати клавішу [Enter].
4. В вікні системи набрати програму або внести необхідні зміни у програму.
4. Запустити програму на виконання: для цього в меню системи вибрати пункт Run
9. В зошит переписати результат роботи програми ( рядки, що були виведені на екран)
10. Якщо необхідно (за вказівкою викладача) записати свою програму на диск у вигляді файлу – для цього необхідно вийти в меню системи, вибрати пункт File и виконати команду Save з указівкою імені свого файлу.
11. Покинути систему Borland Pascal 7.0 – для цього необхідно увійти у меню системи, вибрати пункт File и виконати команду Exit.
ПРИКЛАД ВИКОНАННЯ ЗАВДАННЯ:
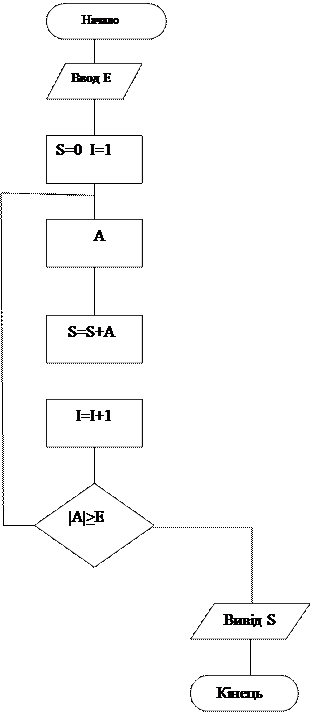
Приклад № 1 Скласти схему алгоритму и програму по ньому для обчислення суми членів ряду

с точністю до члена ряду, меньшего Е=10-3.
Схема алгоритму: Код програми:
1-й варіант текста програми за допомогою циклу з
постумовою “repeat\until”
Program primer;
Var I : integer;
A, S, E : real;
Begin
Writeln (введіть значення Е’);
Readln (E);
S = 0 ;
i = 1;
repeat
begin
A = 1/((2*i – 1) * (2*i + 1)) ;
S = S + A;
i = i + 1;
end;
until ABS(A)>=E ;
writeln ( 'Сума дорівнює:’, S);
end.
2-й варіант текста програми за допомогою циклу з передумовою “While \ do”
Program primer
Var I : integer;
A, S, E : real;
Begin
Writeln (‘Введіть значення Е’);
Readln (E);
S = 0 ; i = 1;
While ABS(A)>=E do
begin
A = 1/((2*i – 1) * (2*i + 1)) ;
S = S + A;
i = i + 1;
end;
writeln ( 'Сума дорівнює: ‘, S);
end.
Результат роботи програми:
Введіть значення Е
1Е-3
Сума дорівнює
12,14
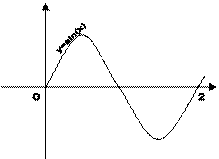
Приклад № 2Скласти схему алгоритму и програму по ньому для визначення значень функції y = sin(x) на відрізку [0,2] з кроком H=0.1.
Program Demo;
Var y,x,a,b,h:real;
Begin
Writeln();
Readln(a,b,h);
X:=a;
Writeln(‘---------------------------------------------------‘);
Writeln(‘ x | f(x) ‘);
 Writeln (‘---------------------------------------------------‘);
Writeln (‘---------------------------------------------------‘);
While x<=b do
Begin
Y:=sin(x);
Writeln(x:4:4, y:5:5);
X:=x+h;
End;
End.
Результат роботи програми:
СКЛАД ЗВІТУ:
1. Тема, мета роботи.
2. Текст завдань для виконання .
3. Порядок виконання роботи.
4. Хід виконання роботи – схема алгоритму, текст програми, результат роботи програми
5. Висновки
КОНТРОЛЬНІ ПИТАННЯ:
1. Яки оператори описують цикл с параметром?
2. Яки оператори описують цикл с предумовою?.
3. Яки оператори описують цикл с постумовою?
4. Який цикл називається ітераційним?
5. Яким чином перевіряється значення логічного виразу в операторі циклу з постумовою?
6. Чи можливо увійти в тіло циклу з параметром мінуя його заголовок?
7. Яким чином можна зробити так, щоб у тілі циклу виконувалося декілька операторів?
8. Яким чином можна організувати безкінечний цикл
Таблиця 3 Варіанти індивідуального завдання № 1 до лаб. роботи № 3
| Номер варіанту
| Знайти суму ряду
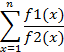
|
| F1(x)
| F2(x)
| x
| n
|
| 1,16
| x+1
| 3Öx+1
| 2.5
|
|
| 2,17
| x
| (2x+1)
| 1.2
|
|
| 3,18
| x2
| x(x+1)
| 0.7
|
|
| 4,19
| cos(2x)
| (2x-1)(2x+1)
| 1.8
|
|
| 5,20
| sin(x)
| x2+2x+3
| 2.6
|
|
| 6,21
| ex
| (2x+1)(x+1)2
| 3.7
|
|
| 7,22
| e2x
| (x+1)(x+2)
| 3.4
|
|
| 8,23
| Tg(x)
| 1+x
| 3.2
|
|
| 9,24
| (x+10)
| Ölnx2
| 1.8
|
|
| 10,25
| sin(5x)
| Ö1+ex
| 1.7
|
|
| 11,26
| cos(3x2)
| Ö5x+ex
| 2.7
|
|
| 12,27
| (-2x)3
| x! ( факторіал n!=1*2*3*..*n)
| 2.2
|
|
| 13,28
| |x|
| x! ( факторіал n!=1*2*3*..*n)
| 0.5
|
|
| 14,29
| Ö|lnx|
| x! ( факторіал n!=1*2*3*..*n)
| 2.1
|
|
| 15,30
| 3Öx
| (2x+1)2
| 0.8
|
|
Таблиця 4 Варіанти індивідуального завдання №2 до лаб. роботи № 3
| Номер варіан-ту
| Функція
| А
| В
| H
| Номер варіанту
| Функція
| A
| B
| H
|
| 1,15
| Ln2x
| 1.3
| 6.5
| 0.5
| 8,22
| Öx2+5
| 1.6
| 4.8
| 0.8
|
| 2,16
| Sin2x+1
| 1.2
| 3.6
| 0.2
| 9,23
| Sin2x
| 1.6
| 2.8
| 0.9
|
| 3,17
| Ex+5
| 1.4
| 4.2
| 1.3
| 10,24
| Ln3x
| 0.2
| 0.8
| 0.04
|
| 4,18
| Arctg2x
| 0.02
| 0.4
| 0.3
| 11,25
| Ölnx2
| 0.2
| 0.8
| 0.01
|
| 5,19
| Ö|lnx|
| 0.5
| 4.6
| 0.5
| 12,26
| Lgx2
| 0.1
| 0.6
| 0.04
|
| 6,20
| Cos 3x
| 0.7
| 1.8
| 0.2
| 13,27
| Öcosx+sinx
| 0.4
| 0.9
| 0.02
|
| 7,21
| 3Öx
|
|
| 1.25
| 14,28
| Ö1+ex
| 0.3
| 0.9
| 0.05
|



 Writeln (‘---------------------------------------------------‘);
Writeln (‘---------------------------------------------------‘);