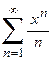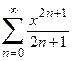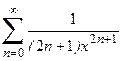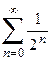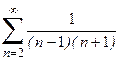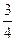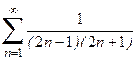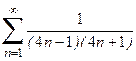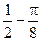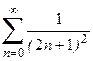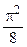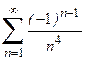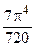1. Приклад використання рекурентної формули un+1 = f(u,n) для послідовного обчислення елементів ряду 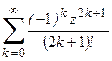 . Знайдемо у загальному вигляді відношення наступного та поточного елементів ряду
. Знайдемо у загальному вигляді відношення наступного та поточного елементів ряду
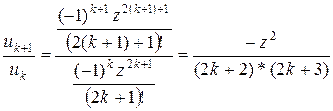
Тоді наступний елемент заданого ряду може бути подано через попередній:
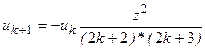
Отриману залежність може бути використано для обчислення будь-якого елемента ряду за умов визначення нульового елемента. Підставлення значення k=0 до загальної формули дозволяє обчислити u0=z, де z задається окремо.
2. Приклад визначення n-ого елемента заданого ряду за допомогою оператора for.
float z,u;
int k,n;
cin<<z<<n; // завдання z та n
u=z; //початковий елемент ряду дорівнює z
for (k=0; k<n; k++)
u*= -z*z/((2*k+2)*(2*k+3)); // визначення наступного елемента
cout<<”\n”<<n<<”-ий елемент ряду = “<<u;
3. Приклад визначення суми перших n елементів заданого ряду за допомогою оператора for.
float z,u,S;
int k,n;
cin<<z<<n;
u=z; //
S=0; //
for (k=0; k<n; k++) { S+=u; //накопичення суми
u*= -z*z/((2*k+2)*(2*k+3));
//обчислення наступного елемента
}
cout<<”\nсума перших “<<n<<” елементів дорівнює ”<<S;
4. Приклад визначення суми елементів заданого ряду із заданою точністю eps за допомогою оператора while.
float z, u, S, eps;
int k;
cin<<z<<eps;
u=z;
S=0; k=0;
while(fabs(u)>=eps) //послідовно обчислювати елементи ряду, поки вони //не менші за задану точність eps
{S+=u; // накопичення суми
u*= -z*z/((2*k+2)*(2*k+3)); // обчислення наступного елемента
k++; //номер поточного елемента збільшити на одиницю
}
cout<<”\n сума елементів з точністю“<<eps<<” дорівнює ”<<S;
5. Приклад повного коду програми, яка дозволяє реалізувати всі пункти завадання для арифметичного ряду 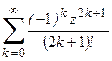 .
.
#include <iostream.h> //підключення бібліотеки введення - виведення
#include <math.h> //підключення бібліотеки математичних функцій
void main()
{char Pr; //змінну використовують для вибору номера пункту
do //оператор do – while використовують для реалізації багаторазового
//виконання пунктів меню
{ cout<<”\nУведіть номер пункту: ”;
cout<<”\n1 - Обчислити| n - ий| елемент заданого арифметичного ряду ”;
cout<<”\n2 - Обчислити суму n перших елементів заданого ряду”;
cout<<”\n3 -Обчислити значення суми арифметичного ряду з точністю Eps”;
cout<<”\n4 - Вихід\n”;
cin>>Pr;
switch(Pr)
{ case ‘1’: //визначення n–ого елемента
{ float z,u;
int k,n;
cin>>z>>n;
u=z;
for (k=0; k<n; k++)
u*= -z*z/((2*k+2)*(2*k+3));
cout<<”\n”<<n<<”-ий елемент ряду = “<<u;}
break;
case ‘2’: //визначення суми n елементів
{ float z, u, S;
int k, n;
cin>>z>>n;
u=z;
S=0;
for (k=0; k<n; k++)
{ S+=u;
u*=-z*z/((2*k+2)*(2*k+3));
}
cout<<”\n Cума перших “<<n<<”елементів дорівнює ”<<S; }
break;
case ‘3’: //визначення суми елементів із заданою точністю eps
{ float z, u, S, eps;
int k;
cin>>z>>eps;
u=z;
S=0; k=0;
while(fabs(u)>=eps) //
{ S+=u; // накопичення суми
u*= -z*z/((2*k+2)*(2*k+3));
k++;
}
cout<<”\nCума елементів з точністю“<<eps<<”дорівнює” <<S;
cout<<”\nПеревірка отриманої суми:”
<<“\nЗначення функції розкладення в точці “<<z << “ дорівнює “ << sin(Z);}
break;
case ‘4’: break;
default: cout<<”\n Невірне значення. Задайте значення від 1 до 4 ”;
}
}
while(Pr!=’4’); //продовжувати цикл, поки значення заданої ознаки не //дорівнюватиме 4
}
Зміст|вміст,утримання| звіту щодо лабораторної роботи №1
1. Титульна сторінка |аркуш|: назва дисципліни; номер і найменування роботи; прізвище, ім'я, по батькові студента; дата виконання.
2. Поставлення завдання|задачі|.
3. Математичний розрахунок формул рекурентної залежності.
4. Лістинг основної програми, де має бути вказано, в якому місці та яка функція викликається|спричиняються|.
5. Результати порівняння сум ряду, отриманих відповідно до другого та третього пунктів завдання, зі значенням контрольної функції розкладення.
Варіанти завдань до лабораторної роботи №1|задавань|
Таблиця 1.1
| Варіант
| Сума
| Контроль
|
| Вихідні дані
| Функція розкладення
|
|
|
|
|
|
| 1.
| 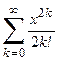
| x =2, e = 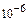
| ch(x)
|
| 2.
| 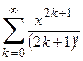
| x =1.5, e = 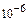
| sh(x)
|
| 3.
| 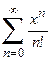
| x =3, e = 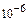
| 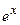
|
| 4.
| 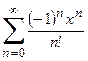
| x =3, e = 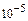
| 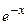
|
| 5.
| 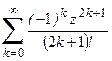
| z =0.5236, e = 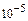
| sin(z)
|
| 6.
| 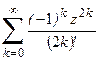
| z =1.047, e = 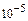
| cos(z)
|
| 7.
| 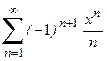
| x = - 0.5, e = 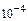
| ln(1+x)
|
| 8.
| 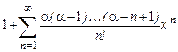
| x =0.5,
a =2.5, e = 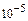
| 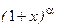
|
| 9.
| 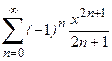
| x = - 1, e = 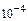
| Arctg(x)
|
| 10.
| 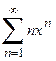
| x = - 0.2, e = 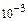
| 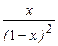
|
|
|
|
|
|
| 11.
| 
| x =0.5, e = 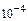
| 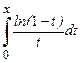
|
| 12.
| 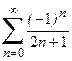
| e = 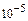
| 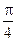
|
| 13.
| 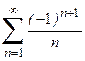
| e = 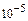
| Ln2
|
| 14.
| 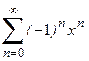
| x = 0.7, {|x| <1},
e = 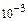
| 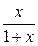
|
| 15.
| 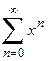
| x = -0.7, {|x| < 1},
e = 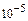
| 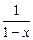
|
| 16.
| 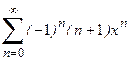
| x = 0.5, {|x| < 1},
e = 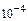
| 
|
| 17.
| 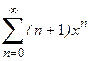
| x = -0.8 {|x| < 1},
e = 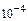
| 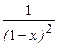
|
| 18.
| 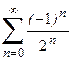
| e = 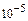
| 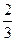
|
| 19.
| 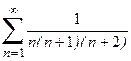
| e = 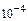
| 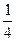
|
| 20.
| 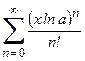
| x =5 {"x} , e = 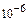
| 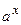
|
| 21.
| 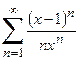
| x =1 { x > 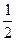 }, e = }, e = 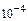
| Lnx
|
| 22.
| 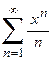
| x = -1{-1£ x < 1},
e = 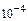
| -ln(1-x)
|
|
|
|
|
|
| 23.
| 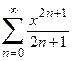
| x = -0.5 {|x| < 1},
e = 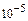
| Arth x
|
| 24.
| 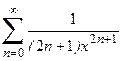
| x = 0.5 {|x| < 1},
e = 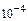
| Arcth x
|
| 25.
| 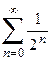
| e = 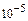
| 2
|
| 26.
| 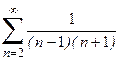
| e = 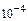
| 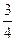
|
| 27.
| 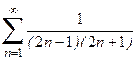
| e = 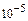
| 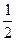
|
| 28.
| 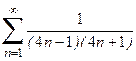
| e = 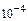
| 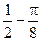
|
| 29.
| 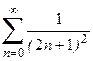
| e = 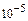
| 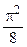
|
| 30.
| 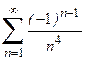
| e = 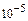
| 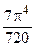
|


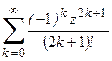 . Знайдемо у загальному вигляді відношення наступного та поточного елементів ряду
. Знайдемо у загальному вигляді відношення наступного та поточного елементів ряду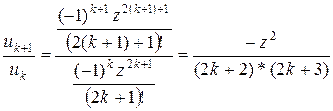
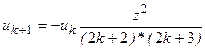
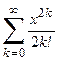
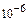
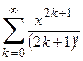
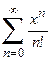
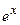
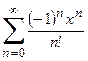
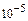
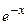
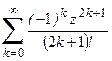
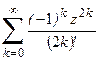
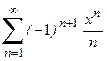
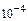
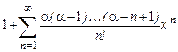
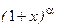
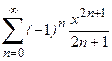
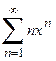
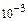
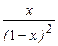

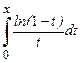
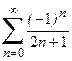
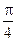
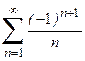
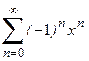
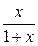
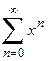
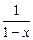
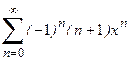

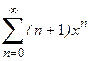
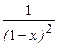
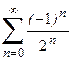
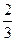
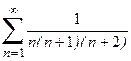
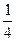
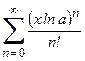
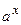
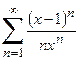
 }, e =
}, e =